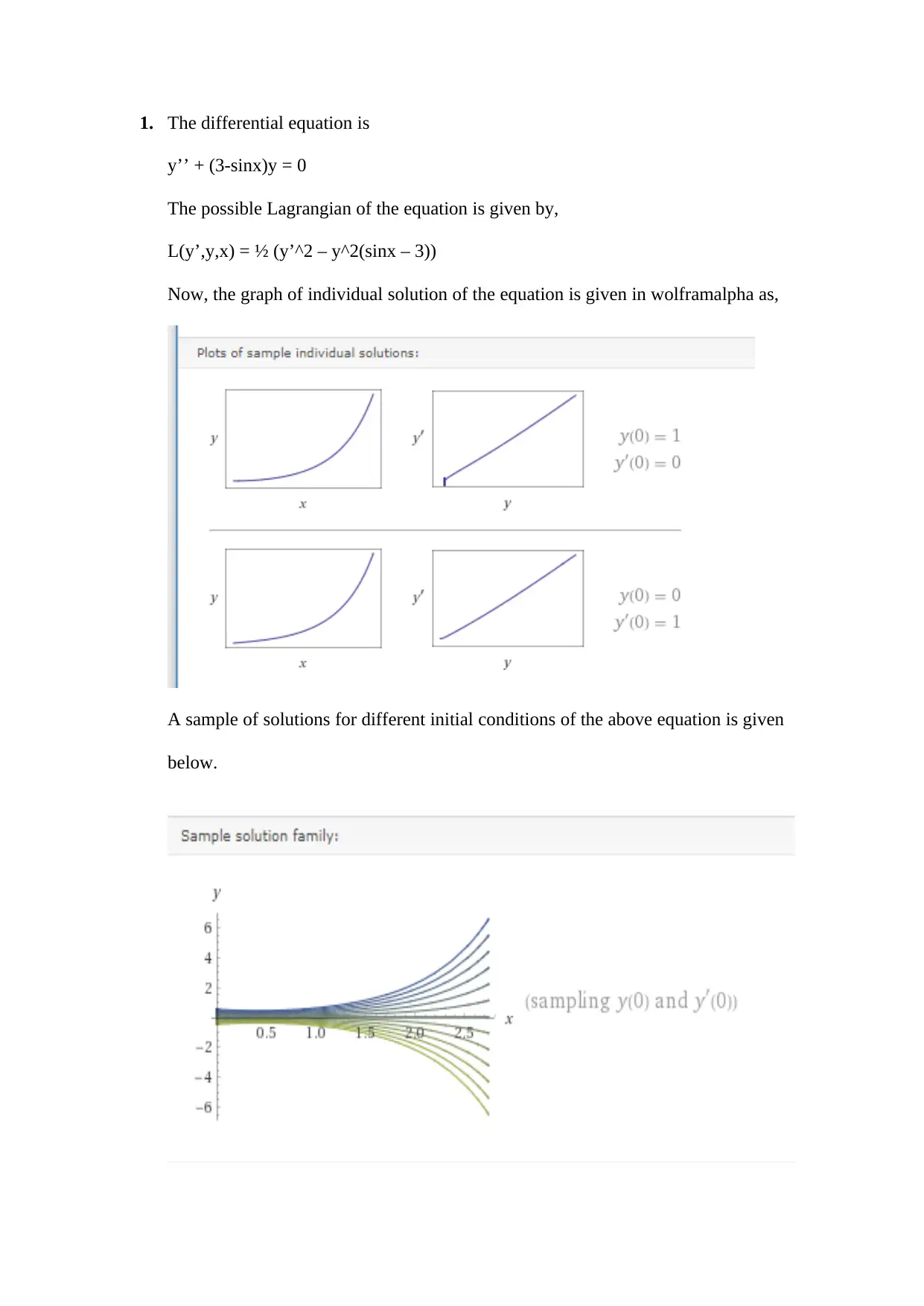
Analysis of Differential Equations in Physics Assignment Solution

This document provides a detailed solution to a physics assignment focusing on differential equations. The solution explores the properties of solutions to these equations, including the number of zeros and the impact of initial conditions. It examines the Hermite equation, providing solutions and analyzing the behavior of the solutions under different conditions. The assignment also involves the use of Sturm-Liouville equations, and the Gauss error function, and polynomial functions. The solution includes a step-by-step breakdown of the problem-solving process and the application of relevant concepts. The analysis involves the use of specific values and the evaluation of the approximate form of the solution at a specific point. The solution also discusses how initial conditions affect the solution of the differential equation.

1. The differential equation is
y’’ + (3-sinx)y = 0
The possible Lagrangian of the equation is given by,
L(y’,y,x) = ½ (y’^2 – y^2(sinx – 3))
Now, the graph of individual solution of the equation is given in wolframalpha as,
A sample of solutions for different initial conditions of the above equation is given
below.

Hence, it is seen that the sample solutions have zeros for different x’s as given above.
Hence, all the solutions will have zeros for infinite numbers of x values in the range
[0,2π].
3. The Hermite equation is given by the form,
y’’ – 2xy’ +2αy = 0
i) Now, putting α = 3 in the equation we get
y’’ – 2xy’ + 6y = 0
This equation can be converted in the form of Sturm-Lioville equation which is of
the form
d
dx ( y' ( x )
ex2
) – 6 y ( x )
e
( x2 ) =0
Now, the solution of the equation is given by,
y(x) = c 2 ex2
¿
where, erf(x) is the gauss error function given by,
erfi(x) = imaginary error function given by,
erfi(x) = -ierf(ix), where i = √−1.
c1 and c2 are the constants determined by the initial conditions of the differential
equation.
Now, as the first expression in the solution vanishes only when
¿ ¿ ¿
And the second expression vanishes when (8 x3−12 x) = 0. Now, the above two
expressions vanishes for finite number of zeros, so the solution has finite number
of zeros.
ii) Now, putting y(0) = 0 in the solution of the differential equation we get,

0 = -c2 => c2 = 0
So, the solution becomes
y(x) = c1(8x^3 – 12x)
Now, it is visible that without x=0 there is another two values of x for which y(x)
= 0.
The values of x for which the solution vanishes are
8x^3 = 12x => x = ±sqrt(3/2)
Hence, without x = 0, for the two zeros of the solution are at x = -3/2 and 3/2.
Now, as the value of c1 changes with respect to different initial conditions y’(x) =
0, it is expected that solution has more than two zeros.
4. Now, the hermit equation as provided above has the solution of the form
y(x) = c1 Hα(x) + c2 F1(-α/2 ; ½ ; x^2)
that is a polynomial function of α.
When α = 3, the solution becomes
y(x) = c 2 ex2
¿
Now, evaluating the approximate form of the solution at x = π
Gives y (π) = sqrt(21/2)
Now, sqrt(21/2) = 3.24 < π (proved)