Athabasca University Math 265: Calculus Homework Assignment Solutions

This document provides a comprehensive solution to a Math 265 homework assignment, focusing on the application of differentiation and integration. The solution covers various aspects of calculus, including limits, asymptotes, function analysis (even/odd functions), finding critical values, global maxima and minima, definite and indefinite integrals, and applications such as area under curves and related rates problems. The assignment also includes detailed explanations and step-by-step solutions to ensure a thorough understanding of the concepts. The document aims to provide students with a complete guide to solving calculus problems, making it a valuable resource for exam preparation and homework assistance.

Math 265: Application of Differentiation, Integrals, Application of Integration
Unit 5-7: Application of Differentiation, Integrals, Application of Integrations
Solution.
1. why lim
x→ π
6
tan ( 3 x ), does not exist:
lim
x→− π
6
tan ( 3 x ) =lim
h→ 0
tan 3 ( −π
6 +h ) ¿ lim
h→ 0
tan ( −π
2 + 3 h )¿ lim
h→ 0
tan (−π
2 )
¿−∞
Thus, the limit does not exist.
2. U ( x ) = u ( x )
x2 −4 Vertical asymptote : x=2Horizontal asymptote: y =2
U ( x )= u ( x )
x2 −4 = u ( x )
( x−2 ) ( x +2 )
For a Vertical asymptote: x=2, then denominator is x-2=0, thus u(x)
should contain x+2 to cancel out.
For the horizontal asymptote y =2, then the lim
x→ ∞
U ( x )=2
lim
x→ ∞
U ( x ) =
lim
x → ∞
f ( u ( x ) )
x−2 =2 ∴ f ( u ( x ) ) =2 x u ( x ) =2 x ( x +2 )u ( x )=2 x2 +4 x
3. If f(x) is an odd function, then f ( −x ) =−f ( x )
a) F ( x )=x sec ( f ( x ) ) sec (−f ( x ) )=sec ( f ( x ) ) ⟹ sec ( f ( x ) ) is EVEN f ( x )=x is anODD
∴ F (−x )=−x [ sec ( f ( x ) ) ]=−F ( x )
Thus, the function is ODD
b) G ( x )=f (−x ) sin ( x3 ) f (−x ) =−f ( x ) ODDsin ( x3 ) isODD
∴ G ( −x ) =−f ( x ) [ −sin ( x3 ) ] =G( x )

Math 265: Application of Differentiation, Integrals, Application of Integration
Thus, the function is EVEN
4. If f ( x ) = √ cos ( x ) −x
a) The critical values can be calculated in the interval [ – π
2 , 0 ]
d
dx ( f ( x ) ) = d
dx ( √cos ( x )−x )=0 let u=cos ( x )−x¿ df
du . du
dx
df
du = d
dx √ u= 1
2 √ u
du
dx = d
dx ( cos ( x ) −x ) =−sin ( x ) −1 d
dx ( f ( x ) ) = 1
2 √u (−sin ( x )−1 ) = −sin ( x )−1
2 √cos ( x )−x
−sin ( x )−1
2 √ cos ( x )−x =0∴ x=−π
2 critical pont is : (−π
2 , √2 π
2 )
The global (absolute) maxima is (−π
2 , √2 π
2 )
The global (absolute) minima is when x=0, thus ( 0 , 1 )is the absolute
minima.
b) The value where the definite interval, ∫
− π
2
0
√cos ( x )−x dx lies
π
2 (1+ √2 π
2 )=3.53949757
5. If f certifies all the given conditions,

Math 265: Application of Differentiation, Integrals, Application of Integration
Then:
a) The function has an x-intercept in interval (-2, -1) since f(x) is
continuous and f(x) changes from negative to positive
b) The function is not differentiable at x=-2. since f '(x) changes from -
3 to positive abruptly at x=-2
c) The function f has both local maximum and local minimum. The
function f has the local minimum at x=-2 since f ' changes from
negative to positive at x=-2. The local maximum of the function f is
at x=-1 since f ' changes from positive to negative at x=-1
d) Yes, the function f has an inflection point at x=1 since f '' changes
from negative to positive at x=1
e) The function f, does not have vertical asymptote. This is because
the function f is continuous everywhere.
f) The function f, has a horizontal asymptote at y=-1. This is because,
lim
x→ ∞
f ( x ) =−1
6. The area under curves
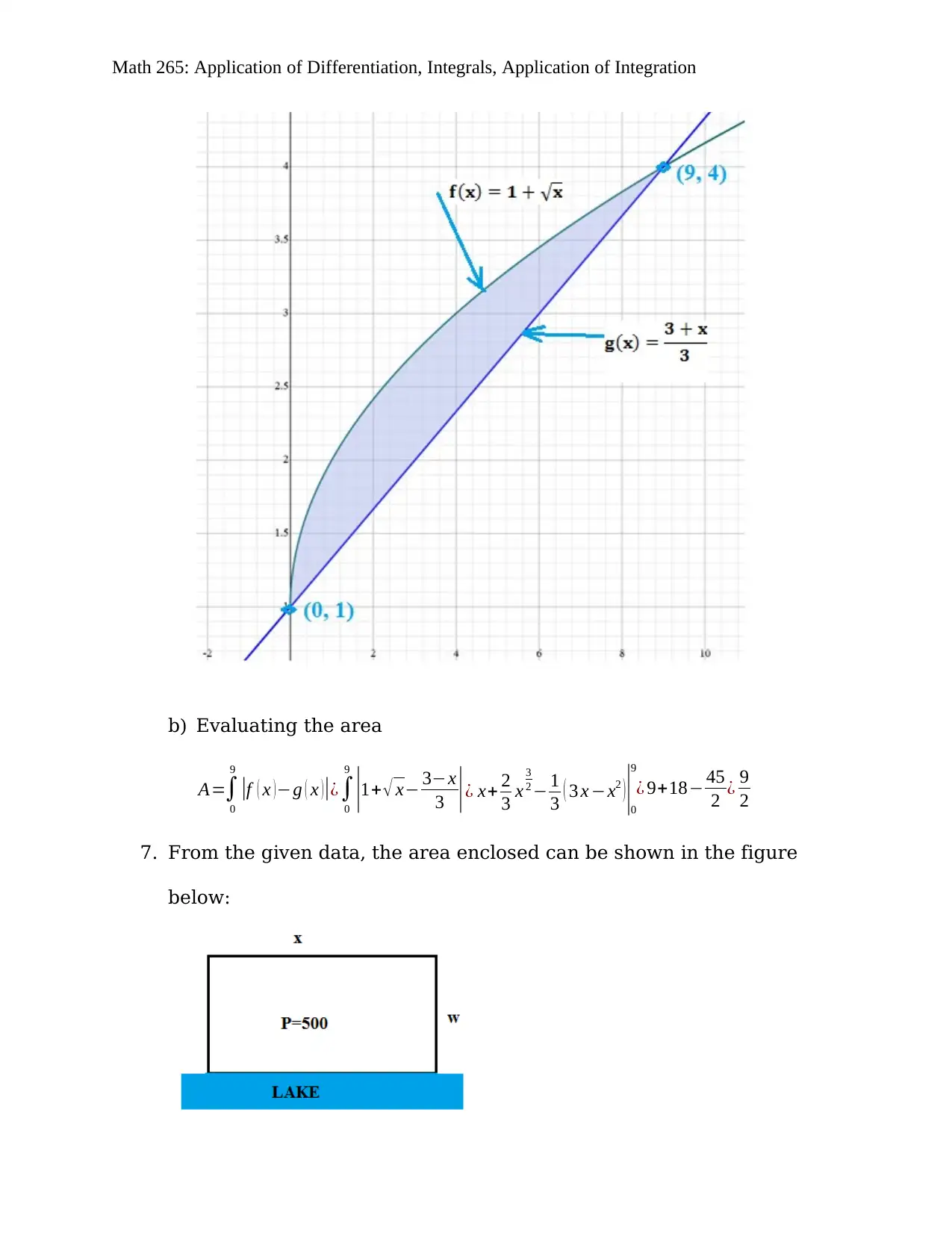
f ( x )=1+ √ x g ( x ) = 3+x
3
a) The sketch of the area is given in figure below

Math 265: Application of Differentiation, Integrals, Application of Integration
b) Evaluating the area
A=∫
0
9
|f ( x ) −g ( x )|¿∫
0
9
|1+ √ x− 3−x
3 |¿ x+ 2
3 x
3
2 − 1
3 ( 3 x −x2 )|0
9
¿ 9+18− 45
2 ¿ 9
2
7. From the given data, the area enclosed can be shown in the figure
below:

Math 265: Application of Differentiation, Integrals, Application of Integration
P ( x , w )=x +2 w=500 x=500−2 w A ( x , w )=xw A ( w )= ( 500−2 w ) w=−2 w2 +500 x
Since the above equation is a parabola that opens downwards, the
vertex is the maximum.
w=−b
2 a = −500
2 ( −2 ) =500
4 =125x=500−2 ( 125 )=250
Thus, the dimension to maximize the area is: x=250 and w=125. The
area will be then 31250
8. The function that satisfies the following
h' ( x )=∫ 2 cos ( 3 x ) sin ( 3 x ) dx¿− cos2 ( 3 x )
3 +Ch' ( 0 )=−cos2 ( 0 )
3 +C= 5
2
−1
3 +C= 5
2 ⟹ C=5
2 + 1
3 = 17
6 h' ( x )=17
6 −cos2 (3 x )
3 h ( x ) =∫ 17
6 − cos2 ( 3 x )
3 dx
¿ 8
3 x− 1
36 sin ( 6 x ) +C2h ( π
2 )= π
3 ⟹ C2= π
3 − ( 8
3 ( π
2 )− 1
36 sin (6 ( π
2 )) )=−π
∴ h ( x ) = 8
3 x− 1
36 sin ( 6 x ) −π
9. Indefinite integral
a) ∫ x √4 x2−5 dx∫ x √4 x2−5 dx= 1
8 ∫ √u du Let u=4 x2−5 ; du
dx =8 x¿ 1
8 (2
3 u
3
2
)+C
¿ 1
8 ( 2
3 ( 4 x2 −5 )
3
2
) +C ¿ ( 4 x2−5 )
3
2
12 +C

Math 265: Application of Differentiation, Integrals, Application of Integration
b) ∫sin2 ( 3 x ) dx∫sin2 ( 3 x ) dx=1
3 ∫ sin2 (u ) du Let u=3 x thus :dx= 1
3 du
¿ 1
3 [ u
2 − cos ( u ) sin ( u )
2 ]+C ¿ x
2 − cos ( 3 x ) sin ( 3 x )
6 ¿ 1
2 x− 1
12 sin ( 6 x ) +C
10. Definite integral
∫
2
5
√ 7 x−2 dx= 1
7 ∫
2
5
√ u du let u=7 x−2 dx= 1
7 du¿ 1
7 ( 2
3 (u
3
2 )|2
5
)= 2
21 ( ( (7 x−2 )
3
2 )|2
5
)
¿ 2
21 ( 33 √33−24 √3 ) ¿ 22 √ 33−16 √ 3
7 ≈ 14.09536647181923
11. The definite integral is correct
12. Using the booth as the reference point, that is at the booth,
distance s0 =0
The car’s position after t seconds when it catches up the track is:
scar =s0 + v0 t + 1
2 a t2
¿ 4 t2
2 =2t2 s0=0 , v0 =0

Math 265: Application of Differentiation, Integrals, Application of Integration
The distance travelled by the truck from the booth;
struck =s0 + v0 t ¿ 2500+50 t scar =struck 2 t2=50t +2500
2 t2−50t−2500=0 Solvingthe quadratc equation
Solving the quadratic equation solves the time taken by the car to
catch up with the truck t= 50± √ 502 +2 ( 4 ) ( 2500 )
2 ( 2 ) ¿ 50 s
The distance from the booth to where the car caught up the truck is:
s=2t2=2 ( 502 )¿ 5000 ft
13. The weight of the chain can be modelled as:
F ( x ) =15 ( 100−x )¿ 1500−15 x
Then, the work done is given as:
W =∫
0
100
F ( x ) dx=∫
0
100
1500−15 x dx¿ 1500 x −15 x2
2 |0
100
¿ 75000 ft ∙lb