Discrete Mathematics: Graph Theory Assignment Solutions and Proofs

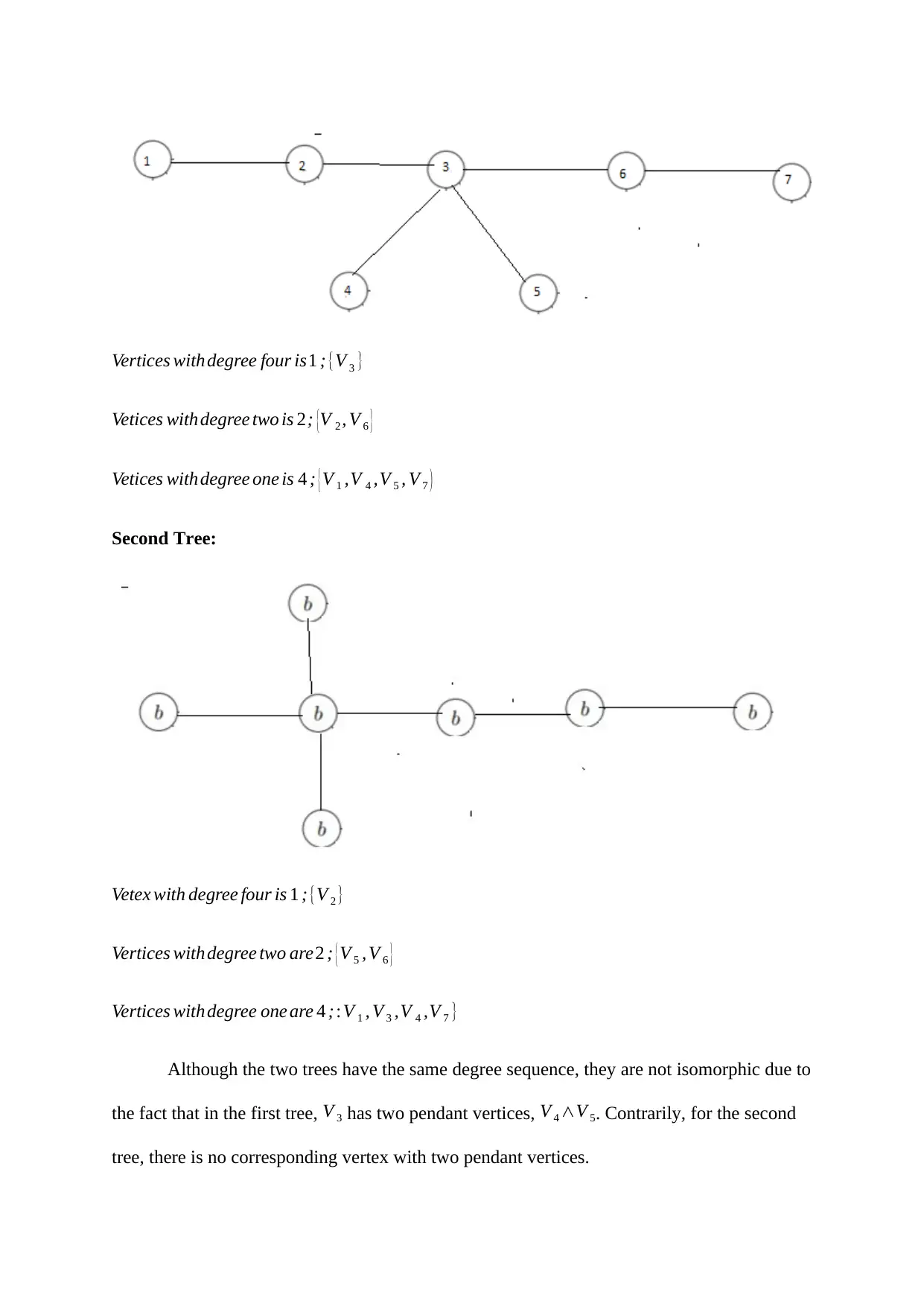
This assignment solution addresses several key concepts in graph theory. Question 1 explores connected components within subgraphs, analyzing their structure and relationships. Question 2 proves that a graph with a unique path between every pair of vertices is a tree, demonstrating the absence of circuits. Question 3 examines degree sequences and their relation to tree structures, providing examples and counterexamples. Question 4 differentiates between isomorphic and non-isomorphic trees, highlighting the importance of vertex properties. Question 5 discusses the number of leaves in a tree, and Question 6 provides a proof that a graph without circuits is a tree, solidifying fundamental graph theory principles. This document is a valuable resource for students studying graph theory and discrete mathematics, offering detailed solutions and explanations.

GAME THEORY
Question 1
a) {a, b, c, d, e}
There are three connected components in the subgraph as shown below:
{a , b , c , d , e }
b) {f, g, h, I, j}
There is one connected component in the subgraph induced by the vertices {f, g, h, I,
j} as shown below:
{f , g ,h , i , j}
c) {a, b, e, h, i}
There three connected components in the subgraph induced by the vertices {a, b, e, h,
i} as shown below:

{a , b , e , h ,i }
d) {c, f, g, I, j}
There are two connected components as shown below:
e) {a, c, d, g, j}
There are five connected components in the subgraph induced by the vertices {a, c, d, g,
j} as shown below:

Question 2
If G is a graph in which any two nodes or vertices are connected by a unique path then G is a
tree.
There is the existence of a path between every pair of vertices so we assume that graph G is
connected. A circuit in a graph implies that there is at least one pair of vertices a and b, such
that there are two distinct paths between a and b. Since G has one and only one path between
every pair of vertices. G cannot have any circuit. Hence graph G is a tree as shown below:
Question 3
a) With the degree sequence, {4,2,1,1,1,1) the following graph can be sketched:
In this case,
d ( V 1 )=4

d ( V 2 )=2
d ( V 3 ) =1
d ( V 4 ) =1
d ( V 5 ) =1
d ( V 6 ) =1
Accordingly, there are a total of 5 edges and 6 vertices connected graph hence a tree.
b) (4, 2, 2, 2, 1, 1)
From the degree sequence, the following graph can be sketched:
d ( V 1 )=4 ,
d ( V 2 ) =d ( V 3 ) =d ( V 4 ) =2 ,
d ( V 5 )=d ( V 6 )=1
The graph is based on 6 edges and 6 vertices connected graph. Accordingly, it is not a tree
because it has a cycle
V 1−V 2 −V 3−V 1
Therefore, with the given degree sequence, there is no a tree.
Question 4
First Tree:

Vertices withdegree four is1 ; {V 3 }
Vetices withdegree two is 2; {V 2 , V 6 }
Vetices withdegree one is 4 ; { V 1 ,V 4 ,V 5 , V 7 )
Second Tree:
Vetex with degree four is 1 ; {V 2 }
Vertices withdegree two are2 ; {V 5 , V 6 }
Vertices withdegree one are 4 ;:V 1 , V 3 ,V 4 ,V 7 }
Although the two trees have the same degree sequence, they are not isomorphic due to
the fact that in the first tree, V 3 has two pendant vertices, V 4 ∧V 5. Contrarily, for the second
tree, there is no corresponding vertex with two pendant vertices.

Question 5
Consider a tree T = (V , E ) ∧u∈ V has degre d
Degree∑ formula gives ∑ of degrees equal¿ twuce thenumber of edges
Let |V |=n .
Thus ,
|E|=n−1.
Therefore, T is true and,
∑ of Degrees=2 ( n−1 ) … … … … … … … … … … … … … … … …(II )
Assuming that the number of leaves∈T are π , we need provethat since π vertices are leaves ,
remaining n−π−1 vertices must have degree at least 2 ;excluding u whose degree is d
Thus ,
∑ of Dgere ≥ π ( 1 ) + ( n−π −1 ) ( 2 ) + d
2 ( n−1 ) ≥ π +2 ( n−π−1 ) +d based on equation(II )
(… π vertices of degree 1 , n−π−1 vetices of degree of at least 2∧one vertex of degree d …)
2 n−2 ≥ π + 2n−2+d
0 ≥−π + d
π ≥d
Hence, the number of leaves are greater or equal to d.
Question 6

Assumethat G is a connected grap h withn vertices∧n−1 edges . ¿ show that G isa tree ,is sufficient ¿ demonstrat
¿ t' supposethat Gcontaints at least one circuit . Giventhat removing an edge ¿ a circuit
does not disconnect a graph , we may remove edges , but no vertices ¿ circuit ∈Guntil
the resulting graph G¿ isa circuit tree .G¿ is a connected graph withn vertices∧has
no circuit .
Accordingly , G¿ is a tree with
n vertices.
Thus , G¿ has n−1 edges ; which is a contrdiction .
Therefore, G does not have circuit hence the proof that G is a tree.