MATH165: Discrete Mathematics I - Problem Set Solutions, Fall 2018

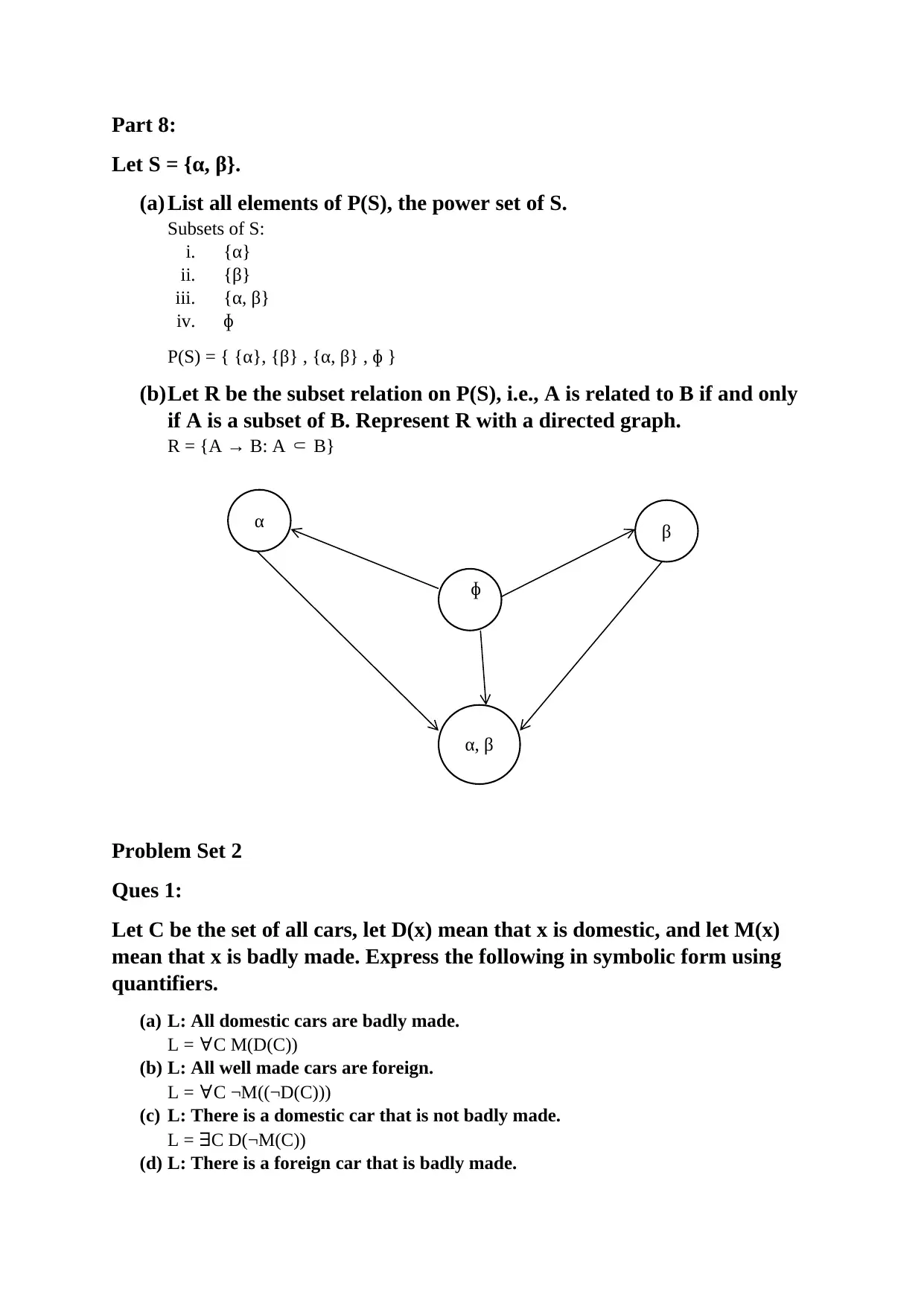
This document contains solutions to several problem sets from a Discrete Mathematics I course (MATH165) offered in Fall 2018. The solutions cover a range of topics, including mathematical induction, proofs of irrationality, set theory operations (union, intersection, difference, etc.), and the representation of sets using set-builder and roster notation. It also includes solutions for problems involving quantifiers, negations, and symbolic logic. Several proofs are provided, including proofs by contradiction and proofs using truth tables. The document also includes solutions for problems related to DeMorgan's Laws, and the validity of arguments. The solutions are presented in a clear and concise manner, with detailed explanations and justifications for each step, making it a valuable resource for students studying discrete mathematics.

Order ID= 905847
Assignment
Final Set
Part 3:
Write the following argument in symbolic form. Then use a truth table to
determine whether the argument is valid. Explain your conclusion
carefully.
Sol: If Mr. Smith bought a yacht, then either he won the lottery or he got a promotion. Mr.
Smith got a promotion and he did not buy a yacht. Therefore, Mr. Smith did not win the
lottery
P: Mr. Smith bought a yacht.
Q: Mr. Smith won the lottery.
R: Mr. Smith got a promotion.
S: If Mr. Smith bought a yacht, then either he won the lottery or he got a promotion.
U: Mr. Smith got a promotion and he did not buy a yacht.
V: If Mr. Smith bought a yacht, then either he won the lottery or he got a promotion. Mr.
Smith got a promotion and he did not buy a yacht. Therefore, Mr. Smith did not win the
lottery
S = P → (Q ˅ R)
U = R ˄ ¬P
V = U → ¬Q
P Q R ¬P ¬Q Q ˅ R S U V
F F F T T F T F T
F F T T T T T T T
F T F T F T T F T
F T T T F T T T F
T F F F T F F F T
T F T F T T T F T
T T F F F T T F T
T T T F F T T F T
Since V is not truth for all the values of P, Q & R, this argument is not valid.
Note: T stands for True and F stands for False.

Part 8:
Let S = {α, β}.
(a) List all elements of P(S), the power set of S.
Subsets of S:
i. {α}
ii. {β}
iii. {α, β}
iv. ɸ
P(S) = { {α}, {β} , {α, β} , ɸ }
(b)Let R be the subset relation on P(S), i.e., A is related to B if and only
if A is a subset of B. Represent R with a directed graph.
R = {A → B: A B}⸦
Problem Set 2
Ques 1:
Let C be the set of all cars, let D(x) mean that x is domestic, and let M(x)
mean that x is badly made. Express the following in symbolic form using
quantifiers.
(a) L: All domestic cars are badly made.
L = ∀C M(D(C))
(b) L: All well made cars are foreign.
L = ∀C ¬M((¬D(C)))
(c) L: There is a domestic car that is not badly made.
L = ∃C D(¬M(C))
(d) L: There is a foreign car that is badly made.
β
α, β
ɸ
α

L = ∃C ¬D(M(C))
Ques 2:
For each of the following quantified statements, give its negation in
symbolic form. Then write an everyday example (in plain English) to
illustrate the original statement and its negation.
(a) (∀xP(x))
¬(∀xP(x))
It signifies that for ALL x, P(x) is true. Eg: All prime numbers are integers.
(b) (∃xP(x))
¬(∃xP(x))
It signifies that there exists one or more values of x such that P(x) is true. Eg: Some
integers are prime numbers.
(c) (∀xP(x) → Q(x))
¬(∀xP(x) → Q(x))
It signifies that for all values of x, if P(x) is true, then Q(x) is also true. Eg: If all the
numbers are prime, then the number is an integer.