Discrete Mathematics Assignment for [University Name] - Fall 2024

This document provides a comprehensive solution to a discrete mathematics assignment, covering a range of topics including functions, relations, graph theory, and trees. The solutions include detailed explanations and step-by-step answers to questions on functions (one-to-one, onto, and bijective), inverse functions, and domain and range determination. Additionally, the assignment explores matrix operations, probability calculations, and graph representations using adjacency matrices. Solutions for graph theory problems include degree sequences, Euler cycles, and the application of algorithms such as Prim's algorithm for finding the minimum spanning tree. Furthermore, the assignment delves into binary search trees and Huffman compression techniques. The document presents clear and concise answers, making it a valuable resource for students studying discrete mathematics.

Running head: Discrete Mathematics
DISCRETE MATHEMATICS
Name of the Student
Name of the university
Name of the author

1Mathematics
Part 1
Answer to the question 1:
a) As the domain of the mentioned relation is {a, b, c, d}.
Here c is an element of the domain set which has two possible range d and a, thus
relation is not a function of the set {a, b, c, d}.
b) As the domain of the mentioned relation is {a, b, c, d}.
Here, every element of the domain set has a defined range, thus this relation is a
function of the set {a, b, c, d}.
c) As the domain of the mentioned relation is {a, b, c, d}.
Here, every element of the domain set has a defined range, thus this relation is a
function of the set {a, b, c, d}.
d) As the domain of the mentioned relation is {a, b, c, d}.
Here, every element of the domain set has a defined range, thus this relation is a
function of the set {a, b, c, d}.
e) As the domain of the mentioned relation is {a, b, c, d}.
Here, every element of the domain set has a defined range, thus this relation is a
function of the set {a, b, c, d}.
Answer to the question 2:
a) The inverse of the function is f (A) is f-1(A) = {(e, a), (d, b), (b, c), (a, d), (d, e)}.
b) The inverse of the function is f (A) is f-1(A) = {(a, b), (d, c), (c, a), (a, d), (b, e)}.
c) The inverse of the function is f (A) is f-1(A) = {(a, a), (c, b), (b, c), (d, d), (e, e)}.
Answer to the question 3:
a) f(x) = 1/x
x = all the real numbers. Hence the answer will come in decimal form.

2Mathematics
f(x)= 1/2 = 0.5 where x= 2
Hence it is not a function.
b) f(x)= y such that y2 = x
For x = 2
y = √ 2
Hence, it is not a function for real number
c) f(x) = x2-1
Where x= 2
f(2)= 4 – 1
=3
Hence it is function for all real number.
Answer to the question 4:
a) The domain of the function is the set of all bit strings.
Domain= {0, 1, 00, 01, 10, 11, 000, 001, 0101, 011,….}
Co-domain= {0, 1, 00, 01, 10, 11, 000, 001, 0101, 011,….}
The range of this function is the set of all numbers of zeros in the bit string.
b) The function is f(x) = x2-3, domain of this function is (-∞ < x < ∞), interval notation
is (-∞, ∞). Range is f(x) ≥ -3, [-3, ∞]
Answer to the question 5:
a) One to one
f(x) = -3x+7
f(a) = f(b), a=b
-3a+7 = -3b+7

3Mathematics
a=b (hence it is one to one)
Onto
Let us assume,
f(x) = y belongs to all real numbers,
f(x) = y
-3x+7 = y
-3x = y-7
x = y-7/-3
Putting value of x in the equation, where x = y-7/-3
f(x) = -3(y-7/-3)+7
f(x) = y (proved)
The mentioned function is a bijective function since it satisfies the both one to one and onto.
b) One to one
f(x) = x2-2x+1
f(a) = f(b), if a = b
a2-2a+1 = b2-2b+1
a2-2a+2b-b2=0 (not proved)
hence this equation is not bijective.
c) One to one
f(x) = 3x3-3
f(a) = f(b) if a = b
3a3-3 = 3b3-3

4Mathematics
1
2
3
4
x
y
z
a3 = b3
a=b (Proved)
Onto
f(x) = 3x3-3,
f(x) = y belongs to all real numbers R
f(x) = y
3x3-3 = y
3x3 = y+3
x3 = y+3/3
x = 3
√ y +3/3
Now, putting the value of x in the function where, x = 3
√ y +3/3
f(x) = 3*(y+3/3)-3
f(x) = y (proved)
The mentioned function is a bijection function since it satisfies the both one to one and onto.
Answer to the question 6
a) R = {(1, x), (2, y), (3, z)}

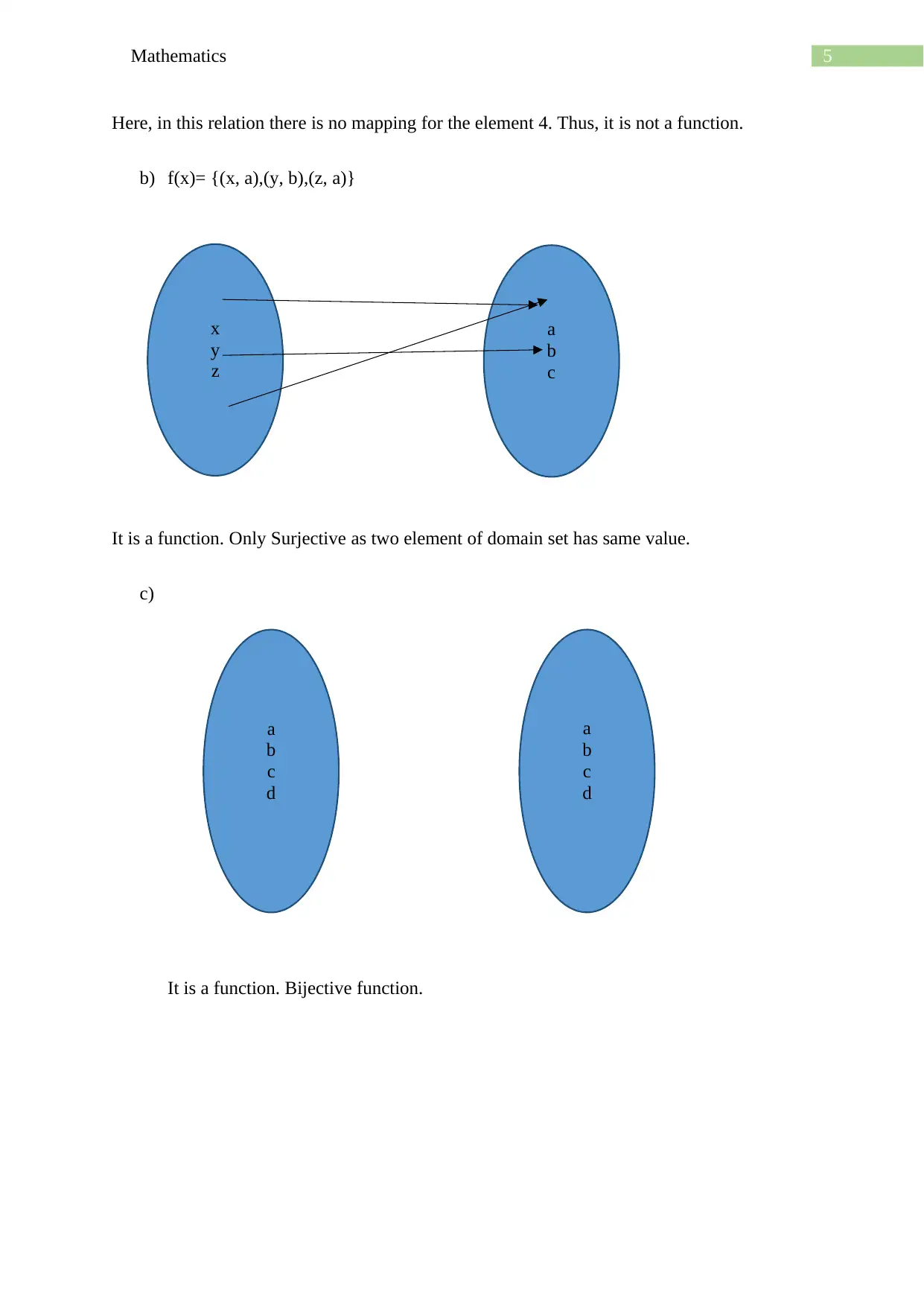
5Mathematics
x
y
z
a
b
c
a
b
c
d
a
b
c
d
Here, in this relation there is no mapping for the element 4. Thus, it is not a function.
b) f(x)= {(x, a),(y, b),(z, a)}
It is a function. Only Surjective as two element of domain set has same value.
c)
It is a function. Bijective function.

6Mathematics
1
2
3
4
a
b
c
d
d)
It is a function. Surjective only.
Answer to the question 7
a) R = {(1,2), (2, 4),(3, 4),(4, 5)}
The above relation is a function as there every element of the domain set has an actual
value.
b) R = {(1,2), (2, 4),(2, 5),(4, 5)}
It is not a function as an element 2 present in domain set has two possible values.
Hence the actual value cannot be determined.
c) R = {(1,2), (2, 4),(4, 5)}
The above relation is a function as there every element of the domain set has an actual
value.
d) R= A × B
R is a function as the product of A and B will be real numbers which is present in the
set R.
Answer to the question 8
A= 6×4, B= 4×4, C= 5×4, D= 6×6

7Mathematics
a) AD is not defined as the numbers of columns are not equals to the number of rows.
b) AB is defined and the size of the matrix product is 6×4.
c) DA is defined and the size of the matrix product is 6×4.
d) BD is not defined as the number of columns are not equals to the number of rows.
Answer to the question 9
A= [3 2 −1
0 2 −2
5 −1 3 ] B= [ 2 5 3
−1 2 −5
2 −2 1 ]
A+B= [ 5 7 2
−1 4 −7
7 −3 4 ]
AB= [ 2 21 −2
−6 8 −12
17 17 23 ]
Answer to the question 10
P(A)= 0.15, P(B)= 0.31
a) P(Ā)= 0.85
b) P(AUB)= {0.15, 0.31}
c) P(A∩B)= empty set as there is nothing common between these two sets.
Answer to the question 11
a) Whole sample set: {(Black, Black), (black, white), (White, Black), (White, White)}.
b)

8Mathematics
17/20 3/20
16/19 2/19 16/19 2/19
Black White
Black White Black White
0
c) Total ball 20, black ball 17 and 3 white ball.
Probabilities of picking the second ball which colour is white 19C2 = 0.1342105263
d) Probabilities of picking the second ball with the colour is black 19C16 = 0.71578
Part B
Answer to question 1
a) Graph to represent the mentioned adjacency matrix:

9Mathematics
b) Graph to represent the mentioned adjacency matrix:
Answer to the question 2
a) Graph G has 6 vertices, and the degree sequence of the graph G is {5, 3, 2, 2, 2, 2}.
b) Graph G has 6 vertices, and the degree sequence of the graph G is {3, 3, 2, 2, 2, 2}.
c) Graph G has 6 vertices, and the degree sequence of the graph G is {3, 3, 3, 3, 2, 2}.
Answer to the question 3
a)
a b c d e f
a 0 1 1 0 0 0
b 1 0 1 0 0 0
c 1 1 0 1 1 1
d 0 0 1 0 1 0

10Mathematics
e 0 0 1 1 0 1
f 0 0 1 0 1 0
b)
a b c d e f
a 0 1 0 1 0 0
b 1 0 1 0 0 0
c 0 1 0 1 0 1
d 1 0 1 0 1 0
e 0 0 0 1 0 1
f 0 0 1 0 1 0
- a b c d e f
a 0 1 1 0 0 0
b 1 0 1 0 0 1
c 1 1 0 1 0 0
d 0 0 1 0 1 1
e 0 0 0 1 0 1
f 0 1 0 1 1 0

11Mathematics
c)
Answer to question 4
a)
E1 E2 E
3
E4 E
5
E6 E
7
E8
a 1 1 0 0 0 0 0 0
b 1 0 1 0 0 0 0 0
c 0 1 1 1 1 1 0 0
d 0 0 0 1 0 0 0 1
e 0 0 0 0 1 0 1 1
f 0 0 0 0 0 1 1 0