Corporate Finance Case Study: PepsiCo Stock Valuation and DDM Analysis

This case study focuses on valuing PepsiCo stock using the Dividend Discount Model (DDM). It begins by explaining the DDM and its advantages and disadvantages. The assignment then applies three DDM variations: zero-growth, constant-growth, and supernormal growth models, to estimate PepsiCo's intrinsic value. It calculates the average annual and compounded average dividend growth rates from 2008 to 2013. The cost of equity is determined using the dividend growth model. The study then calculates the estimated share values using each DDM variation. Finally, it compares the estimated values with the actual market price to provide investment recommendations (buy, sell, or hold). The analysis suggests selling shares based on the supernormal growth model and provides a detailed breakdown of the calculations and assumptions used in each model, offering valuable insights into stock valuation techniques.

1)
The entire objective of the famous dividend discount model is to value a stock. This
dividend discount model popularly known as DDM computes the stock’s intrinsic
value by using current-dividend paid by the stock, growth-rate of future-dividend and
cost related to common stock (required return). This model uses dividend as the
cash flow to the share holders and find the sum of the PVs (present-value) of all
these cashflows in order to arrive at the stock’s intrinsic value. It is always assumed
that the dividends are linked to the earnings potential of the stock.
2)
Advantages:
It is a quantitative method that is simple and easy to apply with minimal information.
This method is widely use and accepted.
This method has a strong theoretical background as it entirely relies on the sum of
PVs (present-values) of future-dividends.
This method finds the intrinsic value of the stock based upon the required return for
its shareholder.
Disadvantages:
This method is very sensitive to the input parameters like required return and growth
rate. So, a little change in these estimates can lead to huge change in the intrinsic
value found using this method.
This method can only be used for the stable companies that have steady history of
dividend payment.
This method assumes that dividends are growing with the earnings and if there is no
relation between the earnings and dividend then the results of this method can be
misleading.
This method cannot be used if growth rate is more that cost of common stock.
3)
Zero-growth model assumes that all the future dividends will be same as the current
dividend by considering a dividend growth = 0. Here, we assume that the current
dividend of 2.24 will continue forever in future. So, to arrive at the intrinsic value we
used present-value formula of an equal annuity and using discount rate equal to cost
of common stock of 9.1825%.
Formula: Estimated-Value (P) = Current dividend (D)/ Required Return (r)
Where, P: estimated-value
D: current dividend.
r: required-return or cost related to common-stock

Constant-growth model works on the assumption that the present growth rate of
dividend will continue forever. So, it uses the Gordon growth model for calculating
the stock’s the intrinsic value. Here, we will assume that the current growth is equal
to the average annual dividends’ growth rate from the year 2008 to the year 2013
and this rate of growth will remain constant forever.
Formula: Estimated-value (P) = Estimated dividend (D1)/ [Required return (r) –
Constant rate of growth (g)]
Where, P: estimated-value
D1: estimated dividend for the next-period
r: required-return or cost related to common-stock
g: constant rate of growth
Supernormal Growth Model works on the assumption that the current growth rate of
dividends is supernormal and this high growth rate will be there for just few years
and afterwards dividends will grow at lower constant growth rate forever. We have
taken an assumption that the dividends would go up at higher rate of growth for next
four years equal to the average annual dividend growth-rate from the year 2008 to
the year 2013. Afterwards this high-growth period dividends will grow forever at
slower growth rate of 6% forever.
Formula is as follows:
Estimated Value (P) = (D0*(1+g1))/(1+r) + (D0*(1+g1)^2)/(1+r)^2 +
(D0*(1+g1)^3)/(1+r)^3 + (D0*(1+g1)^4)/(1+r)^4 + CV/(1+r)^4
Here, CV stands for Continuing Value which equals to:
(D0*(1+g1) ^4 * (1+g2)) / (r-g2)
P: estimated value
D0: current-dividend in the year 2013
r: required-return or cost involved in common-stock
g1: initial higher rate of growth
g2: 2nd lower and forever rate of growth
4)
Constant-growth model will provide the higher estimated-value. DDM (dividend
discount model) calculates sum of PV (present value) of future-dividend. The future
dividend would be higher in constant-growth model because here we assume that
dividend will rise at some positive growth rate as compared to zero growth rate in
zero-growth model. Also, in constant-growth model dividend is divided by r-g which
is a lower value as compared to zero-model where we divide dividend by only r. So,
this would lead constant-growth model to provide higher estimated-value.

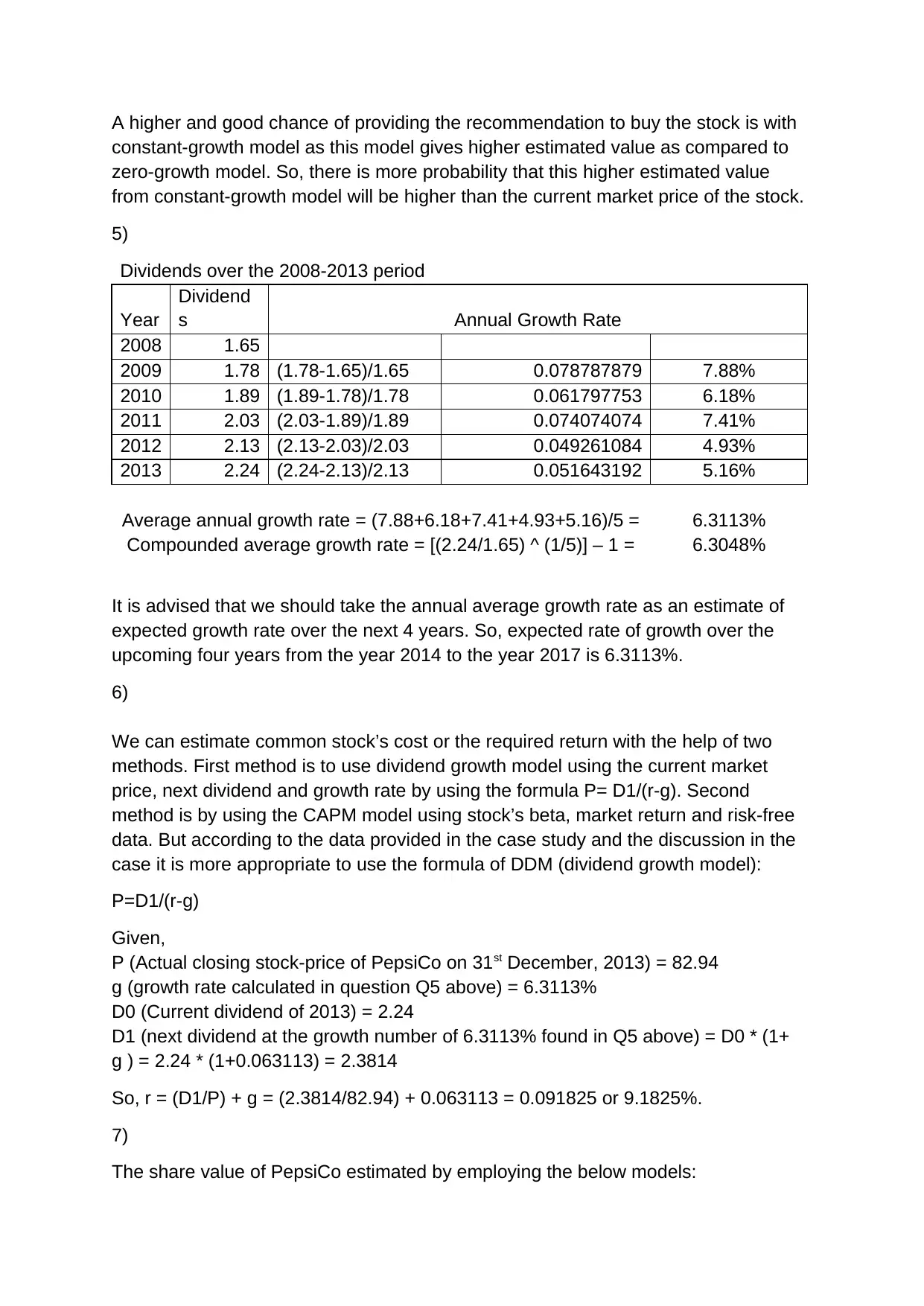
A higher and good chance of providing the recommendation to buy the stock is with
constant-growth model as this model gives higher estimated value as compared to
zero-growth model. So, there is more probability that this higher estimated value
from constant-growth model will be higher than the current market price of the stock.
5)
Dividends over the 2008-2013 period
Year
Dividend
s Annual Growth Rate
2008 1.65
2009 1.78 (1.78-1.65)/1.65 0.078787879 7.88%
2010 1.89 (1.89-1.78)/1.78 0.061797753 6.18%
2011 2.03 (2.03-1.89)/1.89 0.074074074 7.41%
2012 2.13 (2.13-2.03)/2.03 0.049261084 4.93%
2013 2.24 (2.24-2.13)/2.13 0.051643192 5.16%
Average annual growth rate = (7.88+6.18+7.41+4.93+5.16)/5 = 6.3113%
Compounded average growth rate = [(2.24/1.65) ^ (1/5)] – 1 = 6.3048%
It is advised that we should take the annual average growth rate as an estimate of
expected growth rate over the next 4 years. So, expected rate of growth over the
upcoming four years from the year 2014 to the year 2017 is 6.3113%.
6)
We can estimate common stock’s cost or the required return with the help of two
methods. First method is to use dividend growth model using the current market
price, next dividend and growth rate by using the formula P= D1/(r-g). Second
method is by using the CAPM model using stock’s beta, market return and risk-free
data. But according to the data provided in the case study and the discussion in the
case it is more appropriate to use the formula of DDM (dividend growth model):
P=D1/(r-g)
Given,
P (Actual closing stock-price of PepsiCo on 31st December, 2013) = 82.94
g (growth rate calculated in question Q5 above) = 6.3113%
D0 (Current dividend of 2013) = 2.24
D1 (next dividend at the growth number of 6.3113% found in Q5 above) = D0 * (1+
g ) = 2.24 * (1+0.063113) = 2.3814
So, r = (D1/P) + g = (2.3814/82.94) + 0.063113 = 0.091825 or 9.1825%.
7)
The share value of PepsiCo estimated by employing the below models:

(i)
Zero-Growth Model:
Estimated Value (P) = Dividend (D) / Required-return (r)
Where,
P: estimated value.
D: current-dividend in the year 2013 = 2.24.
r is required return or common stock’s cost = 0.091825 or 9.1825%.
So, P = D/r = 2.24/0.091825 = 24.3942.
(ii)
Constant-Growth Model:
P = D1/(r-g)
P: estimated value.
D0: current dividend in 2013 = 2.24.
D1 is estimated dividend in 2014 = D0 * (1+ g) = 2.24 * (1+0.063113) = 2.3814.
r is required return or cost of common stock = 0.091825 or 9.1825%.
g is the constant growth rate calculated in question Q5 above) = 6.3113%
P = D1/(r-g) = 2.3814 / (0.091825-0.063113) = 82.9409.
(iii)
Supernormal Growth Model:
P = (D0*(1+g1))/(1+r) + (D0*(1+g1)^2)/(1+r)^2 + (D0*(1+g1)^3)/(1+r)^3 +
(D0*(1+g1)^4)/(1+r)^4 + CV/(1+r)^4
Here, CV stands for Continuing Value which is equal to (D0*(1+g1)^4 * (1+g2)) / (r-
g2)
P: estimated-value.
D0: current-dividend in 2013 = 2.24.
r is required return or common stock’s cost = 0.091825 or 9.1825%.
g1: initial rate of growth calculated in question Q5 above = 6.3113%.
g2 is second growth rate= 6%.
CV = (D0*(1+g1)^4 * (1+g2)) / (r-g2)
= (2.24*(1+0.063113)^4 * (1+0.06)) / (0.091825 -0.06)
= 95.3023.

P = (D0*(1+g1))/(1+r) + (D0*(1+g1)^2)/(1+r)^2 + (D0*(1+g1)^3)/(1+r)^3 +
(D0*(1+g1)^4)/(1+r)^4 + CV/(1+r)^4
= (2.24*(1+0.063113))/(1+0.091825) + (2.24*(1+0.063113)^2)/(1+0.091825)^2 +
(2.24*(1+0.063113)^3)/(1+0.091825)^3 + (2.24*(1+0.063113)^4)/(1+0.091825)^4 +
95.3023/(1+0.091825)^4
=75.4505.
Estimated value of PepsiCo shares using Zero-growth model = $24.39.
Estimated value of PepsiCo shares using Constant-growth model = $82.94.
Estimated value of PepsiCo shares using Supernormal growth model = $75.45.
8)
Actual closing price of PepsiCo’s stock on 31st December, 2013 = 82.94
Estimated value of PepsiCo shares using Zero-growth model = $24.39.
Based on Zero-growth model, it is advised to the PepsiCo’s potential investors to sell
the shares (go short) as current price of 82.94 is more than the intrinsic price of
$24.39. So, the stock is overvalued and investment advice is to sell its shares.
Estimated value of PepsiCo shares using Constant-growth model = $82.94.
Based on Constant-growth model, it is advised to the PepsiCo’s potential investors
to hold the shares (wait) as current price of 82.94 is equal to the intrinsic price of
$82.94. So, the stock is fairly valued and investment advice is to hold its shares.
Estimated value of PepsiCo shares using Supernormal growth model = $75.45.
Based on Supernormal growth model, it is advised to the PepsiCo’s potential
investors to sell the shares (go short) as current price of 82.94 is more than the
intrinsic price of $75.45. So, the stock is overvalued and investment advice is to sell
its shares.
9)
Actual closing price of PepsiCo’s stock on 31st December, 2013 = 82.94
Estimated value of PepsiCo shares using Supernormal growth model = $75.45.
Based on Supernormal growth model, it is advised to the PepsiCo’s potential
investors is to sell the shares (go short) as current price of 82.94 is more than the

intrinsic price of $75.45. So, the stock is overvalued and investment advice is to sell
its shares.
It is not a good buy according to supernormal growth model. This model assumes
that current growth rate of 6.3113% is supernormal and it will be there for just next
four years and afterwards there will be a lower growth rate of 6% forever. This gives
us an intrinsic value of $75.45 which is less that the actual share price of $82.94. So,
the stock is currently overvalued at its current price as compared to the intrinsic
value given by this supernormal growth model. Therefore, our decision would be to
sell its shares and it is not a good buy.