DMTH137 Discrete Mathematics I Assignment 1 Solution S1 2019

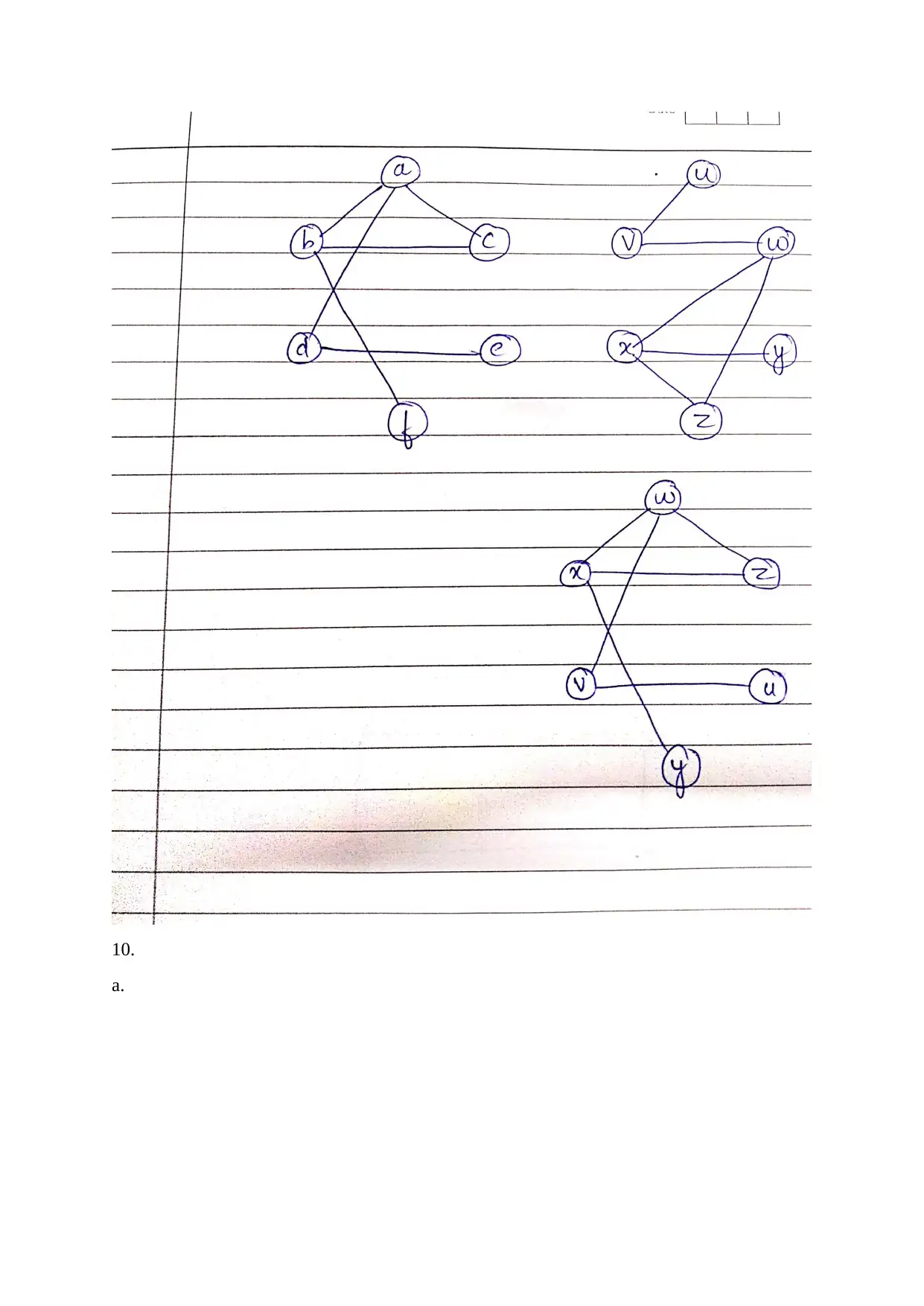
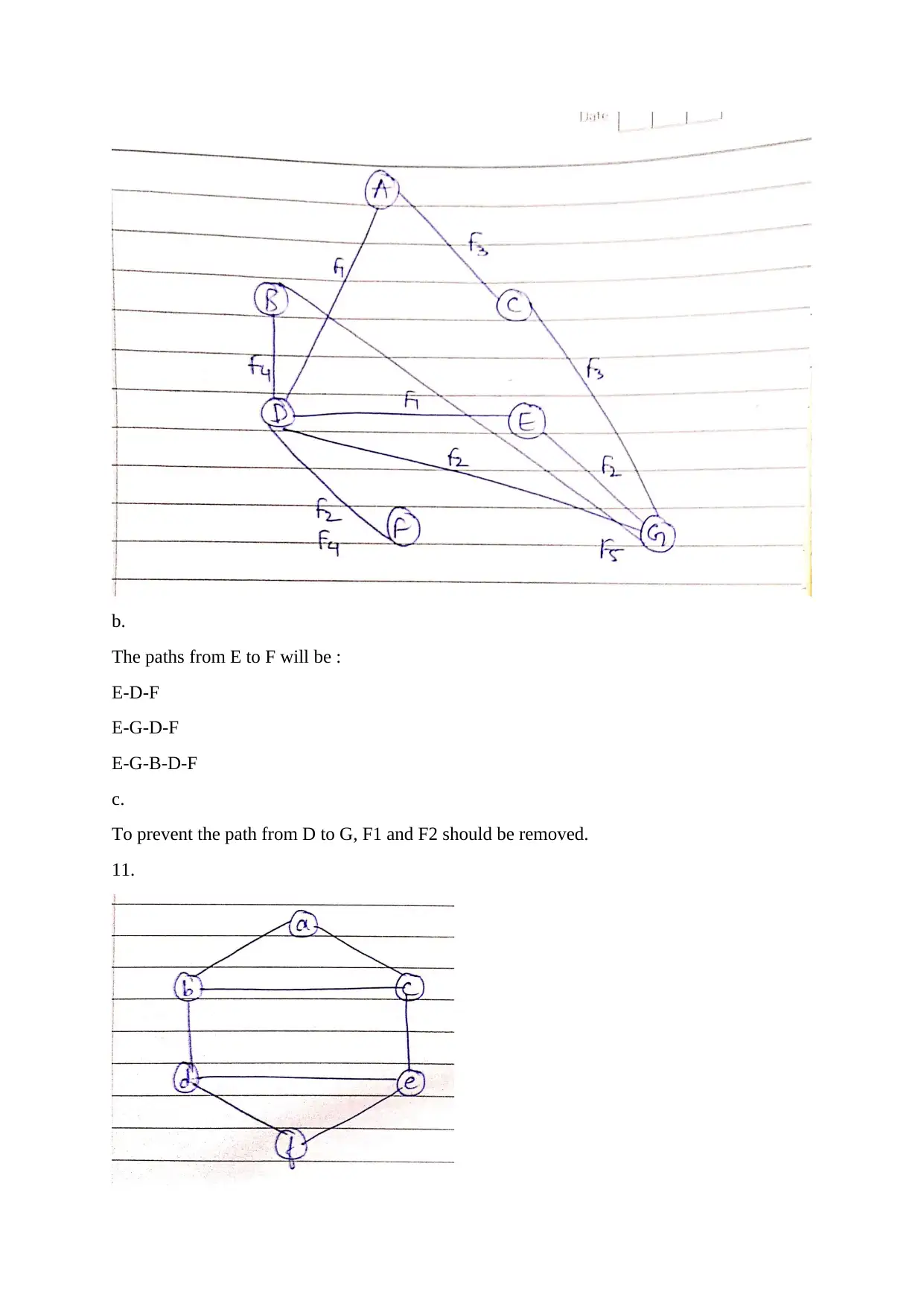
This document provides a detailed solution to Assignment 1 for DMTH137 Discrete Mathematics I at Macquarie University, covering various topics within discrete mathematics. The solution begins with truth tables for logical connectives, including NOT OR (↓), and demonstrates how negation and AND can be expressed using only ↓. It then addresses problems involving quantified statements about computer networks and storage capacity. The assignment continues with proofs and truth tables for quantified statements. The document also explores set theory, including set operations and Venn diagrams. Furthermore, the solution delves into graph theory, covering concepts such as vertex degrees, graph equivalence, and the identification of paths, including Eulerian and Hamiltonian paths. Finally, the solution analyses the correctness of an inductive proof and identifies the flawed step.

1.
a.
p q p OR q p ↓q
0 0 0 1
0 1 1 0
1 0 1 0
1 1 1 0
b.
p q p OR q p ↓q ( p ↓ q)↓( p ↓ q)
0 0 0 1 1
0 1 1 0 0
1 0 1 0 0
1 1 1 0 0
Observation: There is no change in the results. Whether we compute the function one time or
recursively, it does not change the results.
c.
We know that the NOT logic, i.e., negation has only one input. If we short both the inputs of
NOR logic, we result in the implementation of NEGATION.
p q f = p ↓ q
0 0 1
0 1 Invalid case (since both the
inputs can have only same
value)
1 0 Invalid case (since both the
inputs can have only same
value)
1 1 0
We can notice from the above truth table that the NOR logic behaves as the NOT logic.
If we apply the NOR logic on the inverted inputs of p and q, it behaves as the AND logic.
p q ~p ~q g= p ↓ q
0 0 1 1 0
0 1 1 0 0
1 0 0 1 0
1 1 0 0 1

From the above truth table, the AND logic is implemented using the NOR logic.
2.
P(x): x is connected to the network
Q(x): x has at least 100 terabytes of storage
a.
( P ( x ) ∧ Q ( x ) )
b.
P ( x ) ∧Q ( x )
c.
P ( x ) ∨Q ( x )
3.
P ( x , y ) : x2= y
a.
∃ x P (6 , x)
P ( 6 , x ) ⟹ 62=x
x=36
The truth table of this preposition will be a tautology.
b.
∃ x P ( x , 6 )
P ( x , 6 ) ⟹ x2=6
There exists no such whole number whose square is 6. Hence this statement is false.
c.
∀ x ∃ yP ( x , y )
P ( x , y ) ⟹ x2= y
This statement is true as the square of a whole number is always a whole number.
d.
∃ y ∀ xP( x , y )
Same as part (c)
4.
a.

Let n2=4 mbe true
n= √ 4 m
n=2 √m
It is not necessary that n is the multiple of 4.
b.
Let n3 =2 m
n=3
√2m
Hence this statement is not always true.
5.
a.
A− ( B+ C ) +(B ∪ C)
b.
( A ∩ B ) + ( B ∩C ) + ( C ∩ A )−2( A ∩ B ∩C)
c.
U − ( A ∩ B ) + ( B ∩C ) + ( C ∩ A ) −2(A ∩B ∩C )
6.
It is true that if a relation is symmetric and transitive, it must be reflexive.
Example:
Let U = { a , b , c }
R={( a , b ) , ( b , a ) , ( a , a ) ,( b ,b)}
Also, in a relation R if
pRq ,this meansby symmetricity , qRpis aso true .∧by transitivity , pRpis also true .
¿ every element is reflexive ¿ itself . So this statement is true .
7.
In the given table, only source nodes are mentioned and the destination nodes are missing.
We can not find the correct graph with the missing information.
8.
Let the number of vertices be x
No. of edges in the graph = 10
Degrees: 4*2, 3*(x-2)

The sum of the degree of all the vertices is equal to the twice of the number if edges in a
connected graph.
So,
4∗2+3∗( x−2 ) =2∗10
8+3 x−6=20
3 x=18
x=6
9.
Two graphs are said to be equal if they have same vertex set and same set of the connected
edges.
G1 a b c d e f
a 0 1 1 1 0 0
b 1 0 1 0 0 1
c 1 1 0 0 0 0
d 1 0 0 0 1 0
e 0 0 0 1 0 0
f 0 1 0 0 0 0
G2 u v w x y z
u 0 1 0 0 0 0
v 1 0 1 0 0 0
w 0 1 0 1 0 1
x 0 0 1 0 1 1
y 0 0 0 1 0 0
z 0 0 1 1 0 0
Degree matrix of G1 = {3,3,2,2,1,1}
Degree matrix of G2 = {1,2,3,3,1,2}
As we can see from the degree matrix of G1 and G2 that the degrees of all the vertices in both
the graphs is same, irrespective of their order, we can conclude that the graphs G1 and G2 are
equivalent.

10.
a.

b.
The paths from E to F will be :
E-D-F
E-G-D-F
E-G-B-D-F
c.
To prevent the path from D to G, F1 and F2 should be removed.
11.

For having an Eulerian path, the degree of all the vertices of the connected graph must be
even, hence this has no Euler path.
b.
Also, Hamiltonian path also do not exists as for this, the degree of each vertex must at east be
n/2.
12.
S: All computers are built by the same manufacturer.
In the given proof, we can not swap the computer HAL with one of the other computer. This
is the wrong step in this inductive proof.