Agent-Based Simulation of Carpooling for Dublin Traffic Congestion
VerifiedAdded on 2022/11/23
|10
|2125
|288
Project
AI Summary
This project presents an agent-based model designed to simulate carpooling as a solution to traffic congestion in Dublin. The model, built using Netlogo, incorporates geographical datasets and simulates user behavior, considering factors like travel time, cost, and user preferences. The simulation compares scenarios with and without carpooling, analyzing parameters such as travel time, distance, and the number of users served. The results show that carpooling can significantly reduce congestion and improve transportation efficiency, particularly in highly populated areas. The study concludes that the carpooling model is a viable solution to traffic congestion, saving time and money for commuters, and is ideally suited for use in large cities with heavy traffic.

Carpooling as a Solution to Congestion in Dublin 1
CARPOOLING AS A SOLUTION TO CONGESTION IN DUBLIN
By
Name
Course
Institution
Instructor
Location
City
Date
CARPOOLING AS A SOLUTION TO CONGESTION IN DUBLIN
By
Name
Course
Institution
Instructor
Location
City
Date
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Carpooling as a Solution to Congestion in Dublin 2
Carpooling as a Solution to Congestion in Dublin
Carpooling is one of the emerging method people are using to reduce the cost and
time of commuting (Shaheen, Chan, and Gaynor, 2016, p. 168). The technique is eco-friendly
and sustainable in terms of time saved, cost, resource use, and traffic congestion
(Tahmasseby, Kattan, and Barbour, 2016, p. 241). Carpooling involves car-sharing between
people going to similar or different destinations in a particular direction. The process of
carpooling starts with the motive for car-sharing, communication of purpose between various
agents, negotiation, and feedback. The goals for carpooling may be time-saving, convenience,
cost of resources, and other constraints.
The paper will focus on the simulation model of carpooling with the Janus multi-
agent platform. Essentially, it will simulate car-pooling where one agent traveling from point
A to B so will put a request in the model which is also accessible by another person traveling
in the same direction who will pool the same car. The model will tell how much time each of
the agents takes to reach their destinations assuming in the same direction. Therefore, the
model can be used to compare the time and cost taken by bus and car to travel the same route.
Geographical datasets, including accurate maps of Dublin, will be imported from
GeoFabrik into Netlogo (Uri Wilensky , 1999), the platform where the agent-based model
will be created. The scenarios of interest as a proof-of-concept for this research project
include the following experimental setups:
Users’ independently requiring travel from A to B evaluating both bus and carpool
options according to each estimated time, costs –and, if applicable, how many would
carpool.
Different user picks up points, for example, if sharing with four people will it be four
stops or everyone picked up from 1 stop or based on the location assigning closest
pickup points for users.
Carpooling as a Solution to Congestion in Dublin
Carpooling is one of the emerging method people are using to reduce the cost and
time of commuting (Shaheen, Chan, and Gaynor, 2016, p. 168). The technique is eco-friendly
and sustainable in terms of time saved, cost, resource use, and traffic congestion
(Tahmasseby, Kattan, and Barbour, 2016, p. 241). Carpooling involves car-sharing between
people going to similar or different destinations in a particular direction. The process of
carpooling starts with the motive for car-sharing, communication of purpose between various
agents, negotiation, and feedback. The goals for carpooling may be time-saving, convenience,
cost of resources, and other constraints.
The paper will focus on the simulation model of carpooling with the Janus multi-
agent platform. Essentially, it will simulate car-pooling where one agent traveling from point
A to B so will put a request in the model which is also accessible by another person traveling
in the same direction who will pool the same car. The model will tell how much time each of
the agents takes to reach their destinations assuming in the same direction. Therefore, the
model can be used to compare the time and cost taken by bus and car to travel the same route.
Geographical datasets, including accurate maps of Dublin, will be imported from
GeoFabrik into Netlogo (Uri Wilensky , 1999), the platform where the agent-based model
will be created. The scenarios of interest as a proof-of-concept for this research project
include the following experimental setups:
Users’ independently requiring travel from A to B evaluating both bus and carpool
options according to each estimated time, costs –and, if applicable, how many would
carpool.
Different user picks up points, for example, if sharing with four people will it be four
stops or everyone picked up from 1 stop or based on the location assigning closest
pickup points for users.

Carpooling as a Solution to Congestion in Dublin 3
The results of these simulations will be analysed to understand the feasibility of introducing a
carpooling system in Dublin as a convenient way to travel across in Dublin and to explore the
likely impact of carpooling implementation in transportation.
Carpooling Model
An agent is an independent entity with autonomy in decision making on schedules
and needs in traveling. The route schedule is the trips made in a certain period. The model
used in this study considers socio-economic factors such as age, work, income, gender,
education, relationships, vehicle, ownership, and among other sets of data inputs. The car-
pooling model will be represented by:
TRL1 = {Unj=1 rqj, TTRL1}
Where,
TRL1 is the multiple stops car-pool has to stop
Rqj is the number of passenger requests
TTRL1 number of available cars for pooling in the system
The system manager (TRG) integrates all the information gathered from all operating cars for
easy decisions about client pick-up point and most convenient car available for a given route.
TRG = Unj=1 Infotj
Where Infotj is the information shared car-pooling and the system manager which include
destination and preferences as shown below respectively:
Infotj = {Di, Pi}
Di = {D1,D2,……Dn}
Pi = {P1,P2,……Pn}
The system ensures cars-pooling work together and interacts to identify drop
destinations and client mode choice. Each of the car-pooling has the objective of having a
maximum number of trips in the city and transporting as many passengers as possible. The
The results of these simulations will be analysed to understand the feasibility of introducing a
carpooling system in Dublin as a convenient way to travel across in Dublin and to explore the
likely impact of carpooling implementation in transportation.
Carpooling Model
An agent is an independent entity with autonomy in decision making on schedules
and needs in traveling. The route schedule is the trips made in a certain period. The model
used in this study considers socio-economic factors such as age, work, income, gender,
education, relationships, vehicle, ownership, and among other sets of data inputs. The car-
pooling model will be represented by:
TRL1 = {Unj=1 rqj, TTRL1}
Where,
TRL1 is the multiple stops car-pool has to stop
Rqj is the number of passenger requests
TTRL1 number of available cars for pooling in the system
The system manager (TRG) integrates all the information gathered from all operating cars for
easy decisions about client pick-up point and most convenient car available for a given route.
TRG = Unj=1 Infotj
Where Infotj is the information shared car-pooling and the system manager which include
destination and preferences as shown below respectively:
Infotj = {Di, Pi}
Di = {D1,D2,……Dn}
Pi = {P1,P2,……Pn}
The system ensures cars-pooling work together and interacts to identify drop
destinations and client mode choice. Each of the car-pooling has the objective of having a
maximum number of trips in the city and transporting as many passengers as possible. The
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
Carpooling as a Solution to Congestion in Dublin 4
car goal can be modeled as Ntrips, which is between Nmin and Nmin + A. The number of trips
made per day is dependent on time spent per trip and route traffic. These can be defined as
the driver’s preferences.
Nmin < Ntrip < Nmin + Λ
β∗Nmin = A
Where, β is the scalar value.
On the other hand, passenger’s objectives are to save time and hence have speculated upper
and lower bound for the time to reach the destination. Tarrive defines time to spend to reach a
destination using the most convenient route. Treach + λ is the latest time of arrival, and hence
the change in passenger preference changes λ.
Treach ≤ Tarrive ≤ Treach + λ ∗ Treach
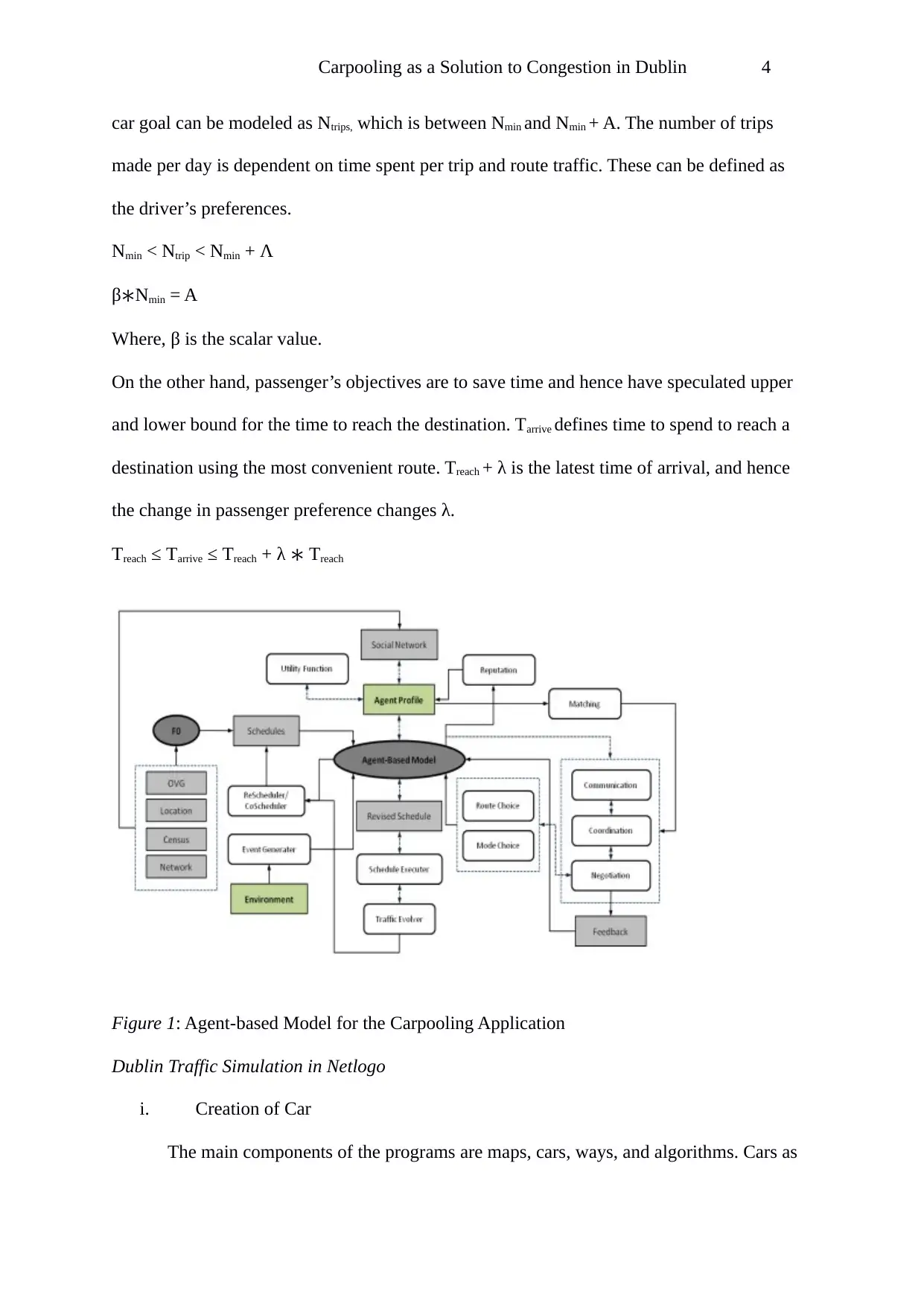
Figure 1: Agent-based Model for the Carpooling Application
Dublin Traffic Simulation in Netlogo
i. Creation of Car
The main components of the programs are maps, cars, ways, and algorithms. Cars as
car goal can be modeled as Ntrips, which is between Nmin and Nmin + A. The number of trips
made per day is dependent on time spent per trip and route traffic. These can be defined as
the driver’s preferences.
Nmin < Ntrip < Nmin + Λ
β∗Nmin = A
Where, β is the scalar value.
On the other hand, passenger’s objectives are to save time and hence have speculated upper
and lower bound for the time to reach the destination. Tarrive defines time to spend to reach a
destination using the most convenient route. Treach + λ is the latest time of arrival, and hence
the change in passenger preference changes λ.
Treach ≤ Tarrive ≤ Treach + λ ∗ Treach
Figure 1: Agent-based Model for the Carpooling Application
Dublin Traffic Simulation in Netlogo
i. Creation of Car
The main components of the programs are maps, cars, ways, and algorithms. Cars as
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Carpooling as a Solution to Congestion in Dublin 5
the agent have distinct attributes and targets. They have identifications which make them
differentiable from others. They are also differentiated in terms of association with
passengers. The cars keep the records of trips made and time taken on each journey from the
start to destination. The simulator provides users with an interface to select cars with a
probability of selecting car-pooler provider. There are three car-pooler providers, including A,
B, and C, which are selected with specific probabilities. The simulator will try to match the
users with car-poolers, and hence, a new itinerary is created. The picks and drops depending
on the number of passengers in the car. The maximum number of passengers is the car is 4
and when it is reached the car is not available in the pool. Below is the screenshot of the
simulation.
The passenger’s options for the car-pooling is given by O = {O1, O2, … On} where O is the
choice of car-pooling in n number of car-pooling in the city. The car choice is dependent on
the destination and most convenient car available.
Figure 2: Screenshot of dynamic carpooling service simulator
ii. Creation of User
the agent have distinct attributes and targets. They have identifications which make them
differentiable from others. They are also differentiated in terms of association with
passengers. The cars keep the records of trips made and time taken on each journey from the
start to destination. The simulator provides users with an interface to select cars with a
probability of selecting car-pooler provider. There are three car-pooler providers, including A,
B, and C, which are selected with specific probabilities. The simulator will try to match the
users with car-poolers, and hence, a new itinerary is created. The picks and drops depending
on the number of passengers in the car. The maximum number of passengers is the car is 4
and when it is reached the car is not available in the pool. Below is the screenshot of the
simulation.
The passenger’s options for the car-pooling is given by O = {O1, O2, … On} where O is the
choice of car-pooling in n number of car-pooling in the city. The car choice is dependent on
the destination and most convenient car available.
Figure 2: Screenshot of dynamic carpooling service simulator
ii. Creation of User

Carpooling as a Solution to Congestion in Dublin 6
The user is the one seeking service from the car-poolers. The simulation needs to
match the users with the most suitable service provider. The clients are identified using IDs as
passengers present; time spends on the trip and distance. The cost depends on the number of
passengers in the car.
iii. Simulation Algorithms
The algorithm is used to match the clients with the most suitable driver. When the
user requests for service, the system matches the user with a driver using the same direction.
The possible cars are listed while the algorithm compares the user origin and destination to
decide on the most suitable car to pool the user. When the user is assigned to the driver, the
driver adds the passenger to the destination list. If there is no suitable driver, users will wait.
initialize:
read in distance matrix, friction factors;
allocate vehicle to stations;
initialize vehicle parameters;
initialize relocation parameters;
generate trips;
for time = tarrive to tarrive + λ {
process event;
update global parameter dataset;
execute relocation process as necessary;
}
customer arrive event {
calculate trip time; (to destination station)
calculate energy to be used;
if (vehicle available) {
assign vehicle;
execute vehicle departure process;
}
else queue customer;
}
vehicle arriveal event {
process vehicle;
reduce vehicle SOC;
}
Relocation arrival event {
process vehicle(s)
(reduce vehicle SOC)
}
iv. High Populated Areas
The user is the one seeking service from the car-poolers. The simulation needs to
match the users with the most suitable service provider. The clients are identified using IDs as
passengers present; time spends on the trip and distance. The cost depends on the number of
passengers in the car.
iii. Simulation Algorithms
The algorithm is used to match the clients with the most suitable driver. When the
user requests for service, the system matches the user with a driver using the same direction.
The possible cars are listed while the algorithm compares the user origin and destination to
decide on the most suitable car to pool the user. When the user is assigned to the driver, the
driver adds the passenger to the destination list. If there is no suitable driver, users will wait.
initialize:
read in distance matrix, friction factors;
allocate vehicle to stations;
initialize vehicle parameters;
initialize relocation parameters;
generate trips;
for time = tarrive to tarrive + λ {
process event;
update global parameter dataset;
execute relocation process as necessary;
}
customer arrive event {
calculate trip time; (to destination station)
calculate energy to be used;
if (vehicle available) {
assign vehicle;
execute vehicle departure process;
}
else queue customer;
}
vehicle arriveal event {
process vehicle;
reduce vehicle SOC;
}
Relocation arrival event {
process vehicle(s)
(reduce vehicle SOC)
}
iv. High Populated Areas
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Carpooling as a Solution to Congestion in Dublin 7
Some parts in Dublin are highly populated while others have high demand as a
destination. People are highly concentrated at the center of Dublin city compared to the
outskirts. The area with a high population is simulated, as shown below.
Figure 3: Screenshot of the field with a high concentration
v. System Output
Besides other information displayed by the system, there are extra outputs with extra
data. In figure 4 below shows, the “num-car-carpoolers” shows the number of carpoolers. The
“cars-pooling” gives the number of cars available for trips. The “num-user-carpooling”
indicates the number of users seeking services. The “users-carpooling” number of users
matched with cars available.
Some parts in Dublin are highly populated while others have high demand as a
destination. People are highly concentrated at the center of Dublin city compared to the
outskirts. The area with a high population is simulated, as shown below.
Figure 3: Screenshot of the field with a high concentration
v. System Output
Besides other information displayed by the system, there are extra outputs with extra
data. In figure 4 below shows, the “num-car-carpoolers” shows the number of carpoolers. The
“cars-pooling” gives the number of cars available for trips. The “num-user-carpooling”
indicates the number of users seeking services. The “users-carpooling” number of users
matched with cars available.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Carpooling as a Solution to Congestion in Dublin 8
Simulated Results
The simulation assumed that users could afford trips, and there is an available car car-
pooling. The results of the simulation will compare the normal trips where traffic jams are
unavoidable with an ideal situation where time and distance covered will be compared.
Therefore, the passenger choice for the car (O) is pegged on the trip characteristics.
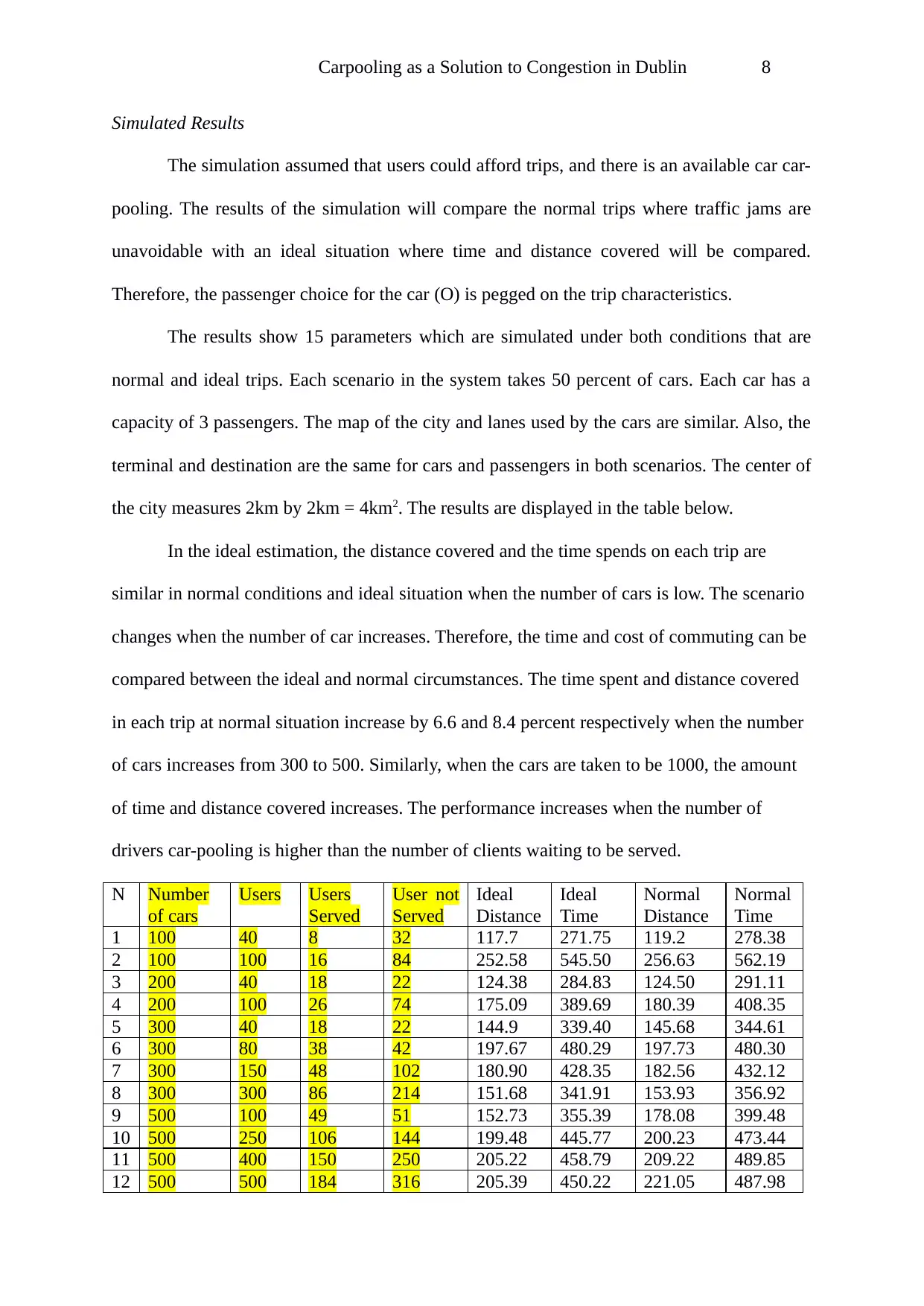
The results show 15 parameters which are simulated under both conditions that are
normal and ideal trips. Each scenario in the system takes 50 percent of cars. Each car has a
capacity of 3 passengers. The map of the city and lanes used by the cars are similar. Also, the
terminal and destination are the same for cars and passengers in both scenarios. The center of
the city measures 2km by 2km = 4km2. The results are displayed in the table below.
In the ideal estimation, the distance covered and the time spends on each trip are
similar in normal conditions and ideal situation when the number of cars is low. The scenario
changes when the number of car increases. Therefore, the time and cost of commuting can be
compared between the ideal and normal circumstances. The time spent and distance covered
in each trip at normal situation increase by 6.6 and 8.4 percent respectively when the number
of cars increases from 300 to 500. Similarly, when the cars are taken to be 1000, the amount
of time and distance covered increases. The performance increases when the number of
drivers car-pooling is higher than the number of clients waiting to be served.
N Number
of cars
Users Users
Served
User not
Served
Ideal
Distance
Ideal
Time
Normal
Distance
Normal
Time
1 100 40 8 32 117.7 271.75 119.2 278.38
2 100 100 16 84 252.58 545.50 256.63 562.19
3 200 40 18 22 124.38 284.83 124.50 291.11
4 200 100 26 74 175.09 389.69 180.39 408.35
5 300 40 18 22 144.9 339.40 145.68 344.61
6 300 80 38 42 197.67 480.29 197.73 480.30
7 300 150 48 102 180.90 428.35 182.56 432.12
8 300 300 86 214 151.68 341.91 153.93 356.92
9 500 100 49 51 152.73 355.39 178.08 399.48
10 500 250 106 144 199.48 445.77 200.23 473.44
11 500 400 150 250 205.22 458.79 209.22 489.85
12 500 500 184 316 205.39 450.22 221.05 487.98
Simulated Results
The simulation assumed that users could afford trips, and there is an available car car-
pooling. The results of the simulation will compare the normal trips where traffic jams are
unavoidable with an ideal situation where time and distance covered will be compared.
Therefore, the passenger choice for the car (O) is pegged on the trip characteristics.
The results show 15 parameters which are simulated under both conditions that are
normal and ideal trips. Each scenario in the system takes 50 percent of cars. Each car has a
capacity of 3 passengers. The map of the city and lanes used by the cars are similar. Also, the
terminal and destination are the same for cars and passengers in both scenarios. The center of
the city measures 2km by 2km = 4km2. The results are displayed in the table below.
In the ideal estimation, the distance covered and the time spends on each trip are
similar in normal conditions and ideal situation when the number of cars is low. The scenario
changes when the number of car increases. Therefore, the time and cost of commuting can be
compared between the ideal and normal circumstances. The time spent and distance covered
in each trip at normal situation increase by 6.6 and 8.4 percent respectively when the number
of cars increases from 300 to 500. Similarly, when the cars are taken to be 1000, the amount
of time and distance covered increases. The performance increases when the number of
drivers car-pooling is higher than the number of clients waiting to be served.
N Number
of cars
Users Users
Served
User not
Served
Ideal
Distance
Ideal
Time
Normal
Distance
Normal
Time
1 100 40 8 32 117.7 271.75 119.2 278.38
2 100 100 16 84 252.58 545.50 256.63 562.19
3 200 40 18 22 124.38 284.83 124.50 291.11
4 200 100 26 74 175.09 389.69 180.39 408.35
5 300 40 18 22 144.9 339.40 145.68 344.61
6 300 80 38 42 197.67 480.29 197.73 480.30
7 300 150 48 102 180.90 428.35 182.56 432.12
8 300 300 86 214 151.68 341.91 153.93 356.92
9 500 100 49 51 152.73 355.39 178.08 399.48
10 500 250 106 144 199.48 445.77 200.23 473.44
11 500 400 150 250 205.22 458.79 209.22 489.85
12 500 500 184 316 205.39 450.22 221.05 487.98

Carpooling as a Solution to Congestion in Dublin 9
13 1000 200 110 90 181.23 428.89 191.74 573.78
14 1000 500 236 264 201.62 469.61 217.74 654.07
15 1000 1000 391 609 210.56 471.08 220.01 675.45
Conclusion
The simulation shows a dynamic carpooling system that can be used to optimally
utilize the transport system available as people share rides and costs of commuting. The
simulation was developed using Netlogo to study the most efficient and convenient method
of commuting in the city of Dublin.
The simulation shows that users have the advantage of car-pooling over other
methods of commuting like personal cars. These are economic advantages like lowers cost of
commuting, save on time, more distance covered in less time. The simulation offers a
solution to the problem of traffic jams, time spent, and distance covered during commuting.
As a result, the model is ideal to be used by highly populated areas like cities where
numerous traffics jam to reduce the number of cars in the city, and hence the time and cost
spend in commuting.
13 1000 200 110 90 181.23 428.89 191.74 573.78
14 1000 500 236 264 201.62 469.61 217.74 654.07
15 1000 1000 391 609 210.56 471.08 220.01 675.45
Conclusion
The simulation shows a dynamic carpooling system that can be used to optimally
utilize the transport system available as people share rides and costs of commuting. The
simulation was developed using Netlogo to study the most efficient and convenient method
of commuting in the city of Dublin.
The simulation shows that users have the advantage of car-pooling over other
methods of commuting like personal cars. These are economic advantages like lowers cost of
commuting, save on time, more distance covered in less time. The simulation offers a
solution to the problem of traffic jams, time spent, and distance covered during commuting.
As a result, the model is ideal to be used by highly populated areas like cities where
numerous traffics jam to reduce the number of cars in the city, and hence the time and cost
spend in commuting.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Carpooling as a Solution to Congestion in Dublin 10
References
Shaheen, S.A., Chan, N.D., and Gaynor, T., 2016. Casual carpooling in the San Francisco
Bay Area: Understanding user characteristics, behaviors, and motivations. Transport
Policy, 51, pp.165-173.
Tahmasseby, S., Kattan, L., and Barbour, B., 2016. The propensity to participate in a peer‐to‐
peer social‐network‐based carpooling system. Journal of Advanced Transportation,
50(2), pp.240-254.
Wilensky, U., 1999. Center for connected learning and computer-based modeling.
In NetLogo. Northwestern University.
References
Shaheen, S.A., Chan, N.D., and Gaynor, T., 2016. Casual carpooling in the San Francisco
Bay Area: Understanding user characteristics, behaviors, and motivations. Transport
Policy, 51, pp.165-173.
Tahmasseby, S., Kattan, L., and Barbour, B., 2016. The propensity to participate in a peer‐to‐
peer social‐network‐based carpooling system. Journal of Advanced Transportation,
50(2), pp.240-254.
Wilensky, U., 1999. Center for connected learning and computer-based modeling.
In NetLogo. Northwestern University.
1 out of 10
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.

