Econometrics Assignment: Regression Models and Hypothesis Testing

This econometrics assignment presents a regression analysis using Microsoft data, exploring concepts such as risk premium and beta values. The analysis includes the development and testing of hypotheses using Wald tests to determine the significance of coefficients. The assignment also calculates and interprets R-squared values, assesses confidence intervals for beta values, and predicts Microsoft's return based on market returns. Furthermore, it extends the analysis to include regression models for other companies like GE, GM, IBM, Disney, and Mobil-Exxon, providing a comparative view of their market behavior. The solution also includes several tables which provides detailed results of the analysis.

Running Header: ECONOMETRICS 1
ECONOMETRICS
Student's name:
Institution:
Professor's name:
Course code:

Econometrics 2
1.
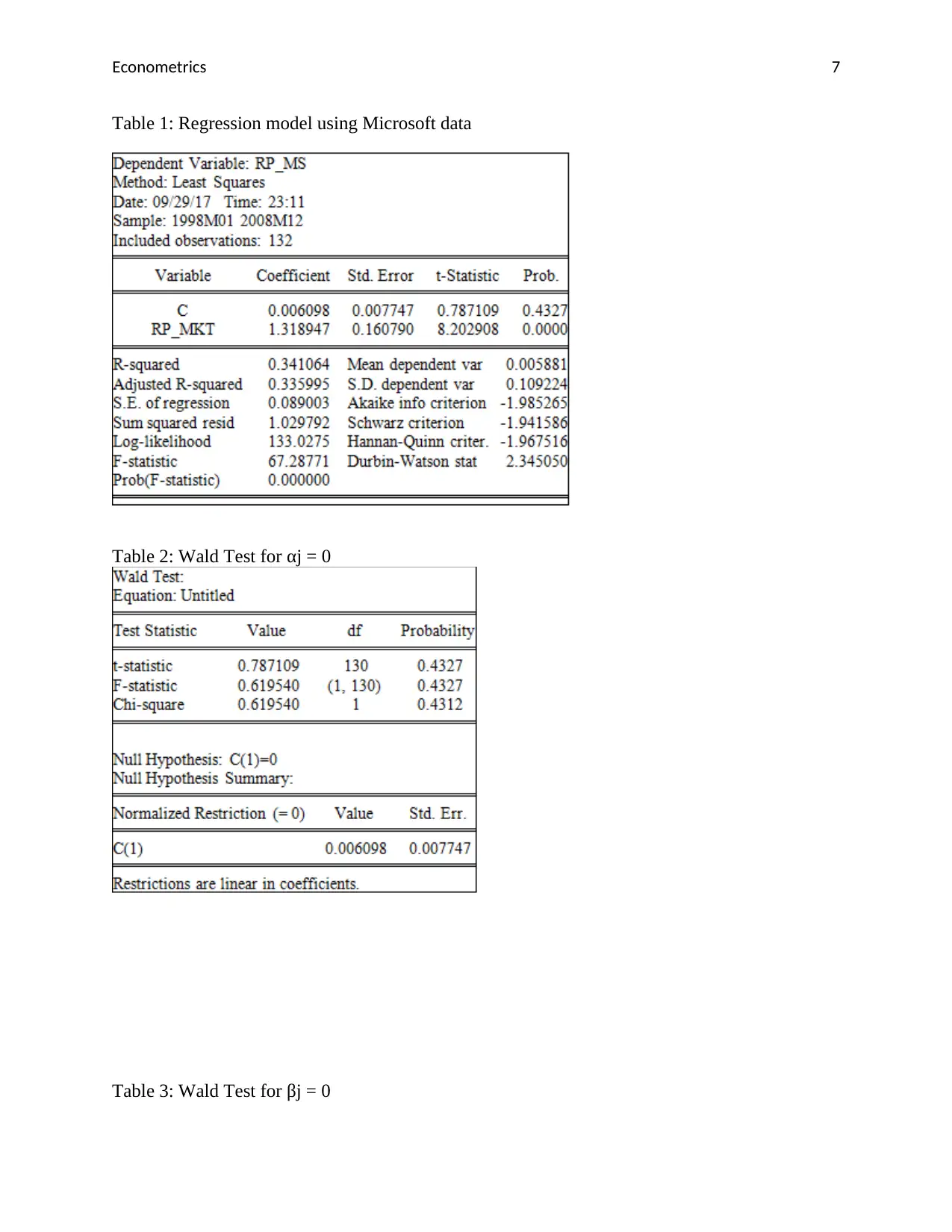
Regression model using Microsoft data
rp_ms = 0.006 + 1.319rp_mkt
Standard Error 0.008 0.161
R2 = 0.34
2.
The beta estimate for risk premium on the market portfolio is 1.319. The beta suggests that when
all other factors are kept constant, when the market portfolio risk premium increases by a unit, it
will result in a 1.319 increase in the Microsoft risk premium. Conversely, the standard error or
the market portfolio risk premium is 0.161. Thus, the standard error suggests that the mean data
points distance from the line fitted is about 0.161.
3.
To test the null hypothesis that αj = 0 for the Microsoft stock, the following hypothesis was
developed:
Ho: αj = 0
H1: αj ≠ 0
The hypothesis was tested using Wald test.
The decision is not to reject the null hypothesis since Wald p-values of t-statistic, F-statistic, and
Chi-square are greater than 0.00. Thus, αj for a security j under market efficiency is equal to 0
(Schwert, 2003). However, the linear restrictions are identical since F-statistics and the Chi-
square value are the same.

Econometrics 3
4.
On the other hand, to test the null hypothesis that βj = 0 for the Microsoft stock, the following
hypothesis was developed:
Ho: βj = 0
H1: βj ≠ 0
The Wald Test was utilized.
The decision derived is to reject the null hypothesis since probability values of t-statistics, F-
statistic, and Chi-square are all 0.00. Thus, βj for a security j under market efficiency is not equal
to 0. However, the linear restrictions are identical since F-statistics and the Chi-square value are
the same.
5.
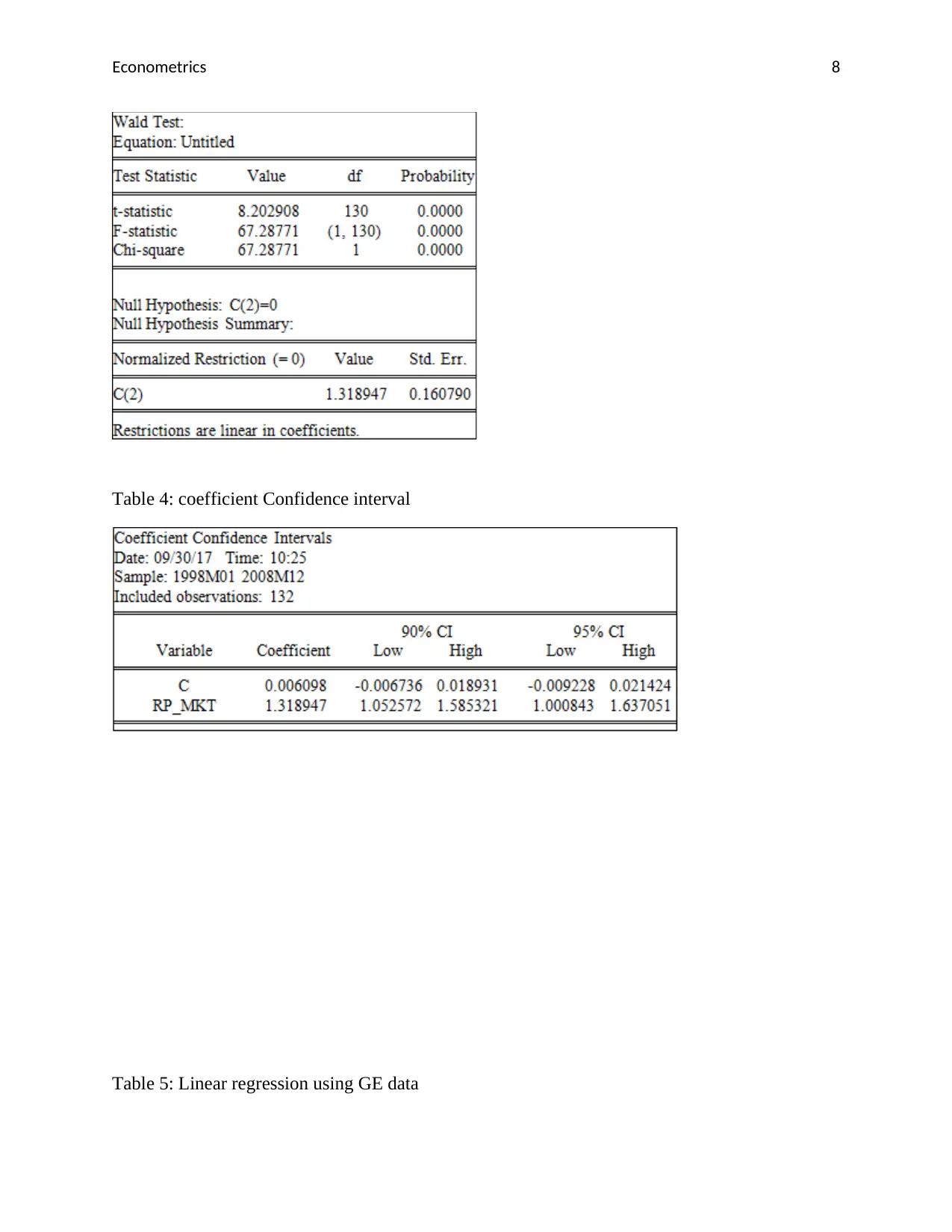
To evaluate the claim that the tech stocks typically have a high beta value, a confidence interval
was used (Altman & Bland, 2011). From the results, it was seen that at 90% confidence interval
the beta ranged from 1.05 to 1.59. On the other hand, at 95% confidence interval, the beta ranged
from 1.0008 to 1.6371. Thus, the tech stock typically has a high beta value (β > 1).
6.
From the regression model, the R2 was 0.34. The R2 for the regression means that the model
explains 34% of the response data around its mean.
7.

Econometrics 4
Risk free rate for December 2008: 0.000025
Market return as at December 2008: 0.21482
Market return as at January 2009 = 0.21482 * 1.01 = 0.216968
Regression model: rp_ms = 0.006 + 1.319rp_mkt
Thus, predicted Microsoft return = 0.006 + 1.319*0.216968
= 0.292181
8.
a) Regression model using GE
rp_ge = -0.001 + 0.899rp_mkt
Standard Errors 0.005 0.099
R2 = 0.39
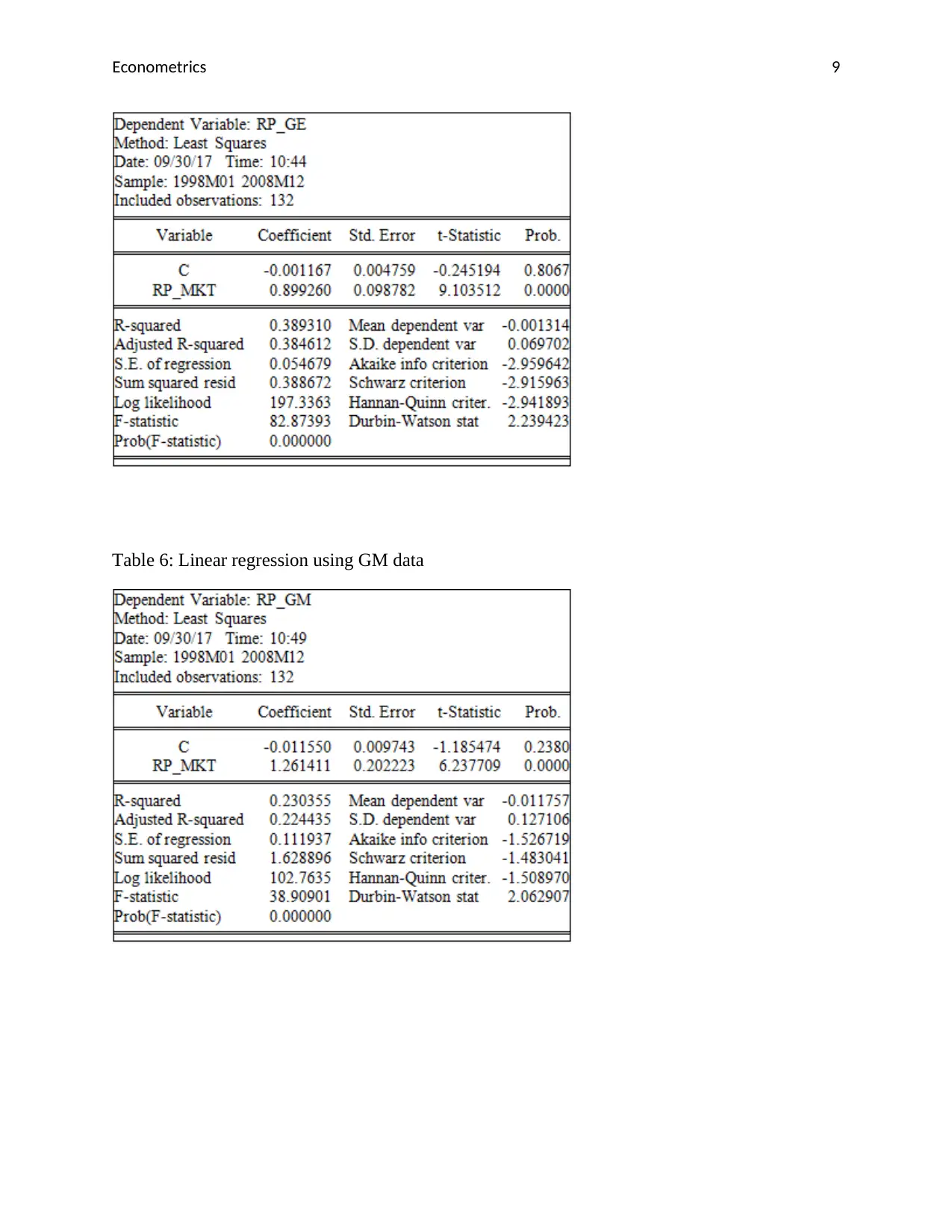
b) Regression model using GM
rp_gm = -0.0116 + 1.261rp_mkt
Standard Errors 0.010 0.202
R2 = 0.23
c) Regression model using IBM
rp_ibm = 0059 + 1.1882rp_mkt
Standard Errors 0.006 0.126
R2 = 0.40
d) Regression model using Disney
rp_disney = -0.0011 + 0.8978rp_mkt
Standard Errors 0.006 0.124

Econometrics 5
R2 = 0.29
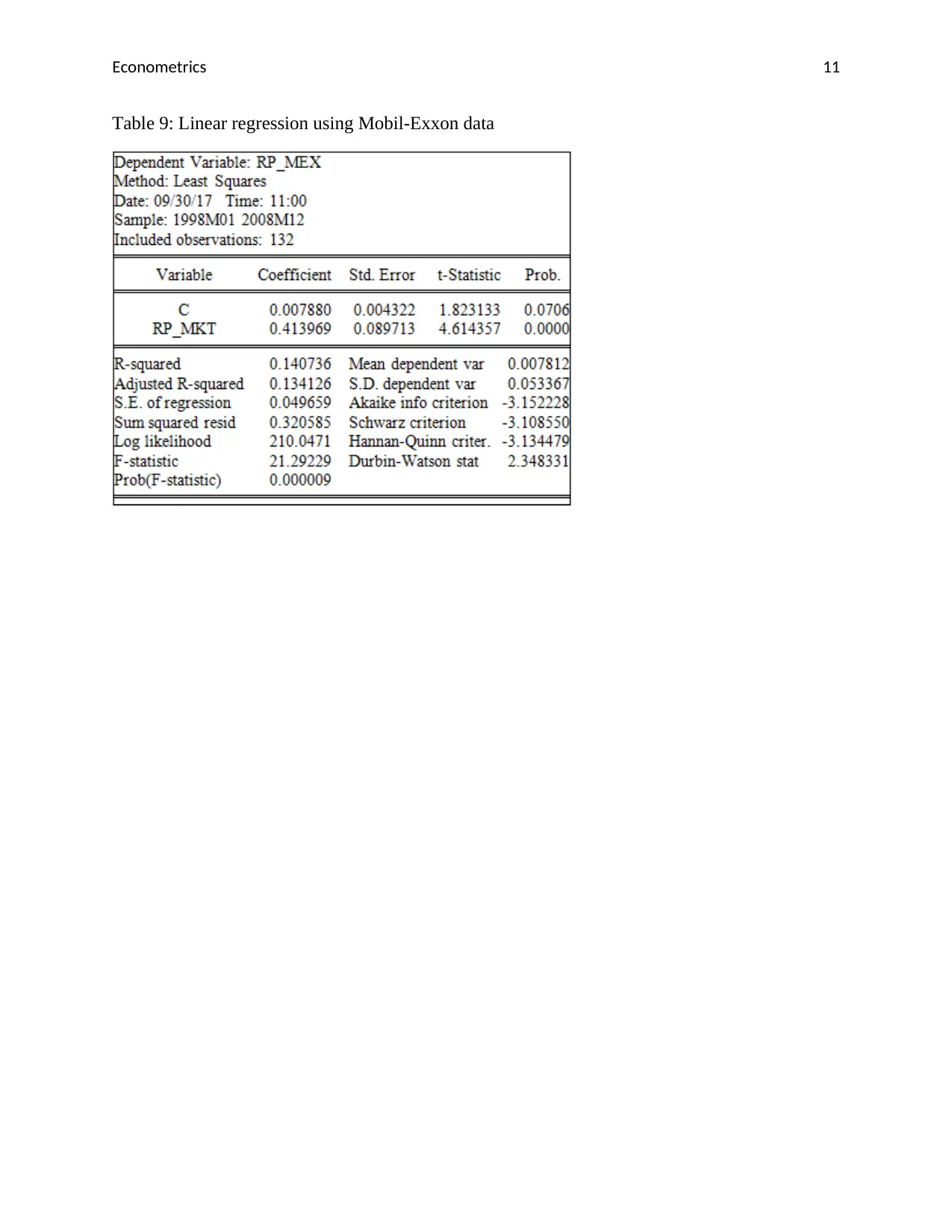
e) Regression model using Mobil-Exxon
rp_mex = 0.0078 + 0.4140rp_mkt
Standard Errors 0.004 0.090
R2 = 0.14
Reference:

Econometrics 6
Altman, D. G., & Bland, J. M. (2011). How to obtain the confidence interval from a P
value. BMJ, 343, d2090.
Schwert, G. W. (2003). Anomalies and market efficiency. Handbook of the Economics of
Finance, 1, 939-974.
Appendix

Econometrics 7
Table 1: Regression model using Microsoft data
Table 2: Wald Test for αj = 0
Table 3: Wald Test for βj = 0

Econometrics 8
Table 4: coefficient Confidence interval
Table 5: Linear regression using GE data

Econometrics 9
Table 6: Linear regression using GM data

Econometrics 10
Table 7: Linear regression using IBM data
Table 8: Linear regression using Disney data

Econometrics 11
Table 9: Linear regression using Mobil-Exxon data