Microeconomics Assignment: Consumer Choice and Cost Functions Analysis

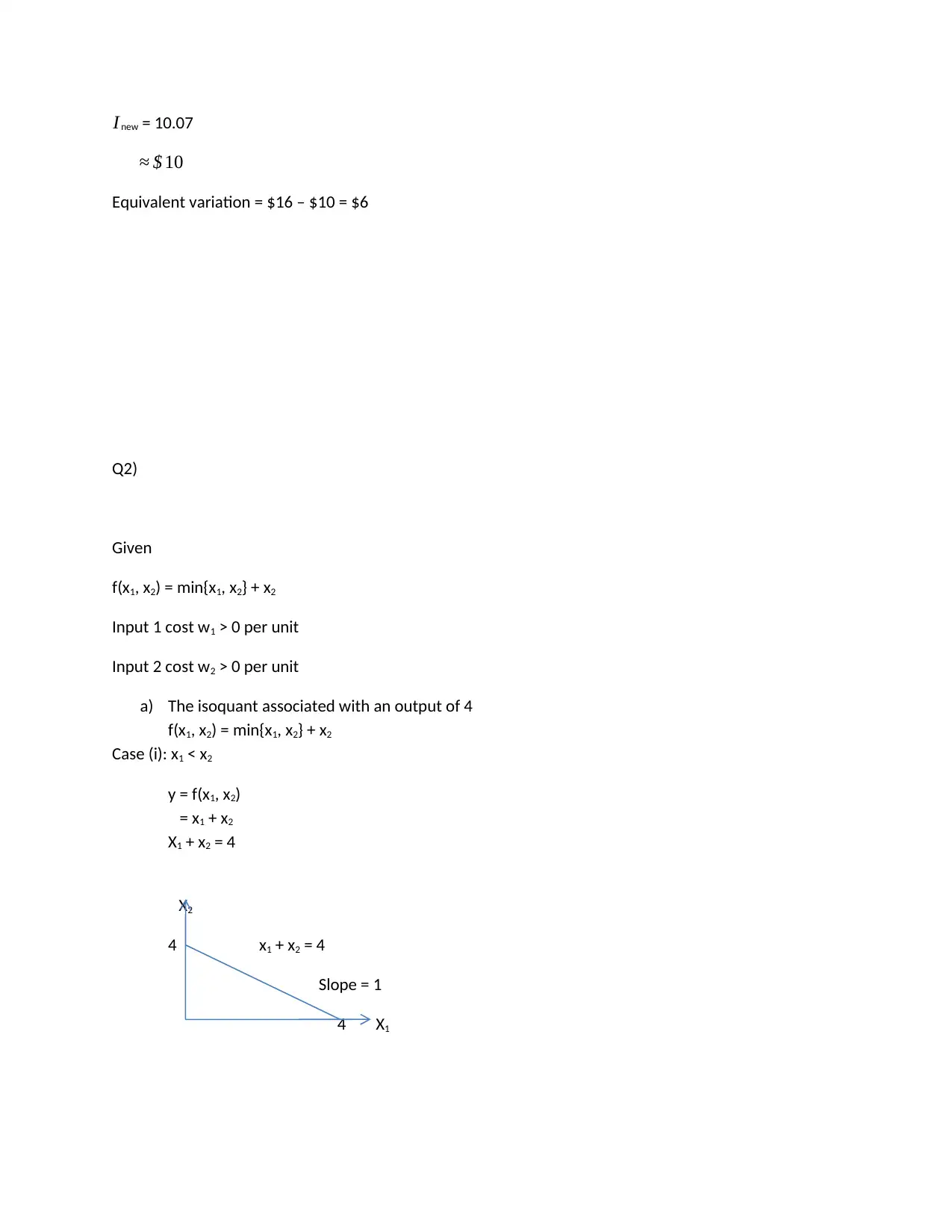
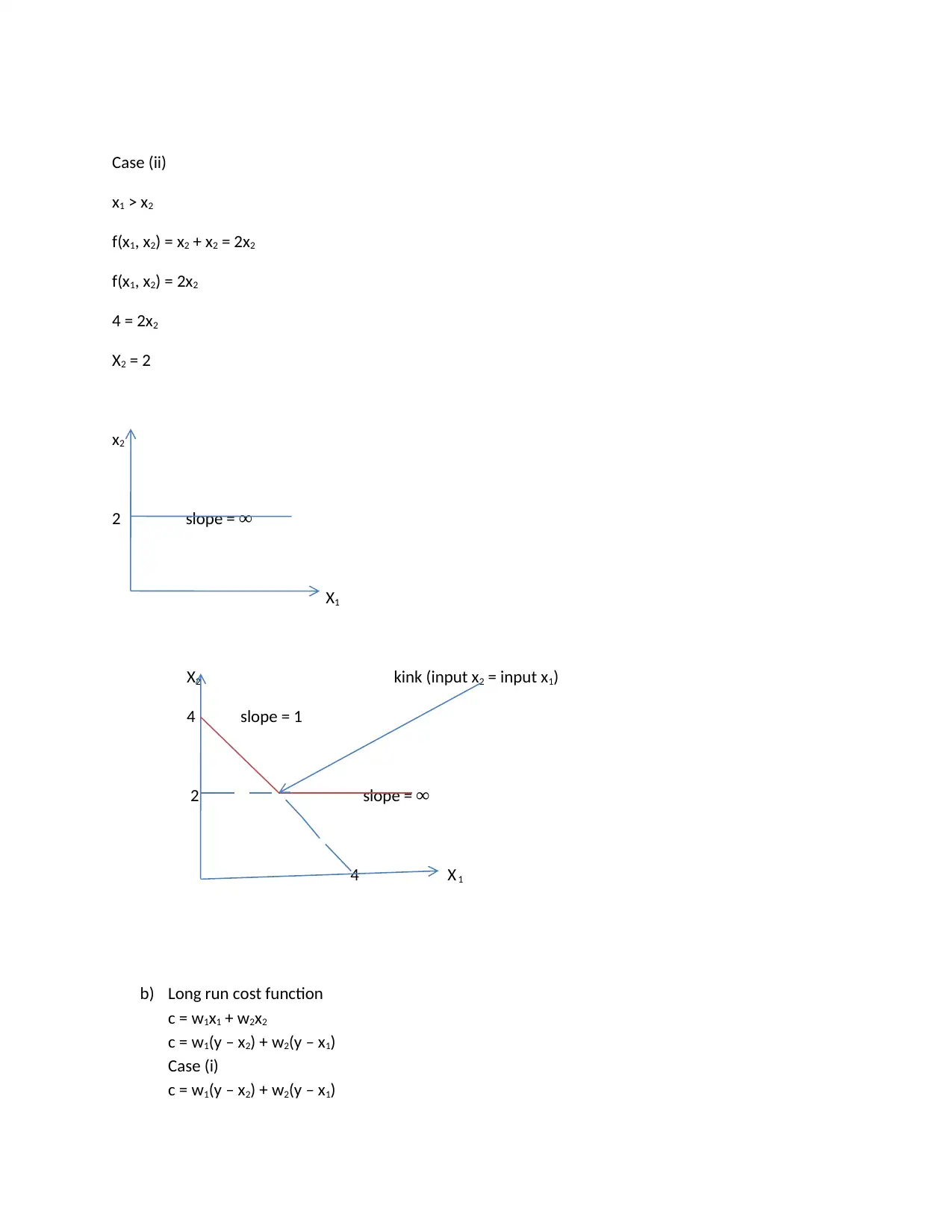
This economics homework assignment addresses core microeconomic concepts including utility functions, consumer choice, and cost analysis. The first question explores utility maximization, calculating compensating and equivalent variations in response to price changes, considering a specific utility function and income levels. The solution details the calculations for both scenarios. The second question delves into cost functions, analyzing a production function with two inputs, and deriving the associated isoquants and long-run cost function. The solution provides a breakdown of the isoquant's shape and derives the long-run cost function based on different input relationships. The assignment provides a comprehensive analysis of consumer behavior and production costs, offering insights into how economic agents make decisions under various constraints.

Solution
Q1a)
If we assume that Alice is consuming two commodities X and Y the utility function given is by;
u ( x , y )=x∝ Y 1−∝, x ≥ 0∧ y ≥ 0.
The general rule shows that we will have a constant budget share demand function of;
X¿= ( ∝
∝ +1−∝ )∗I
PX
, this can be represented as;
X¿=∝ ( I
px )
Similarly,
Y ¿= ( ∝
∝ +1−∝ )∗I
Py
, this can be represented as;
Y ¿=∝ ( I
py )
For this case, income (I) = 16 and px = py = 1. Where the initially the consumption bundle is
x¿=∝¿
(16
1 )=16 ∝ ¿ e initially the consumption bundleis 1. wheremand function of duction function
And y¿= ( 1−∝ )∗16
1 =16−16 ∝
Compensation variation is amount of money that will be given to consumer in order to keep original
bundle. There will be a price change of py from 1 to 4, the new bundle of y will be;
y∗¿ ( 1−∝ ) ∗16
4 =4−4 ∝
The original bundle was 16−16 ∝units of y
The new price of $4 per unit, the bundle will require $16 more than the current income; therefore the
compensating variation is $6.
The money that will be required to buy the old bundle at new price of 4*( 16−16 ∝¿, which is more
than the current income by $16 will be;

4*(16 - 16∝¿ +16 ∝−16=16
64 - 64 ∝+16 ∝−16=16
Collecting like terms together
64 - 64 ∝+16 ∝=16+16
64 - 64 ∝+16 ∝=32
48∝=32
∝= 2
3
b)
Equivalent variation is amount of money that is needed by the consumer in order to buy the same
bundle at the same old price old price that entails a new utility.
Equivalent variation = New income – old income
Demand function for x =
2
3∗I
Px
Demand function for y =
1
3∗I
Py
Utility function, U = X
2
3 ∗Y
1
3
U = [ 2
3∗I
Px ] 2
3
∗[ 1
3 ∗I
Py ] 1
3
= 2
9 ( I )∗( 1
Px ) 2
3∗( 1
Py ) 1
3
Uold income and new price = = 2
9∗16∗( 1
1 ) 2
3 ∗( 1
4 ) 1
3 = 2.2399
2.2399 = = 2
9 ( I (new) ) ∗( 1
1 ) 2
3∗( 1
1 ) 1
3

Inew = 10.07
≈ $ 10
Equivalent variation = $16 – $10 = $6
Q2)
Given
f(x1, x2) = min{x1, x2} + x2
Input 1 cost w1 > 0 per unit
Input 2 cost w2 > 0 per unit
a) The isoquant associated with an output of 4
f(x1, x2) = min{x1, x2} + x2
Case (i): x1 < x2
y = f(x1, x2)
= x1 + x2
X1 + x2 = 4
X2
4 x1 + x2 = 4
Slope = 1
4 X1

Case (ii)
x1 > x2
f(x1, x2) = x2 + x2 = 2x2
f(x1, x2) = 2x2
4 = 2x2
X2 = 2
x2
2 slope = ∞
X1
X2 kink (input x2 = input x1)
4 slope = 1
2 slope = ∞
4 X1
b) Long run cost function
c = w1x1 + w2x2
c = w1(y – x2) + w2(y – x1)
Case (i)
c = w1(y – x2) + w2(y – x1)