EECS 152B Assignment 4: Implementing Sample Rate Conversion in MATLAB

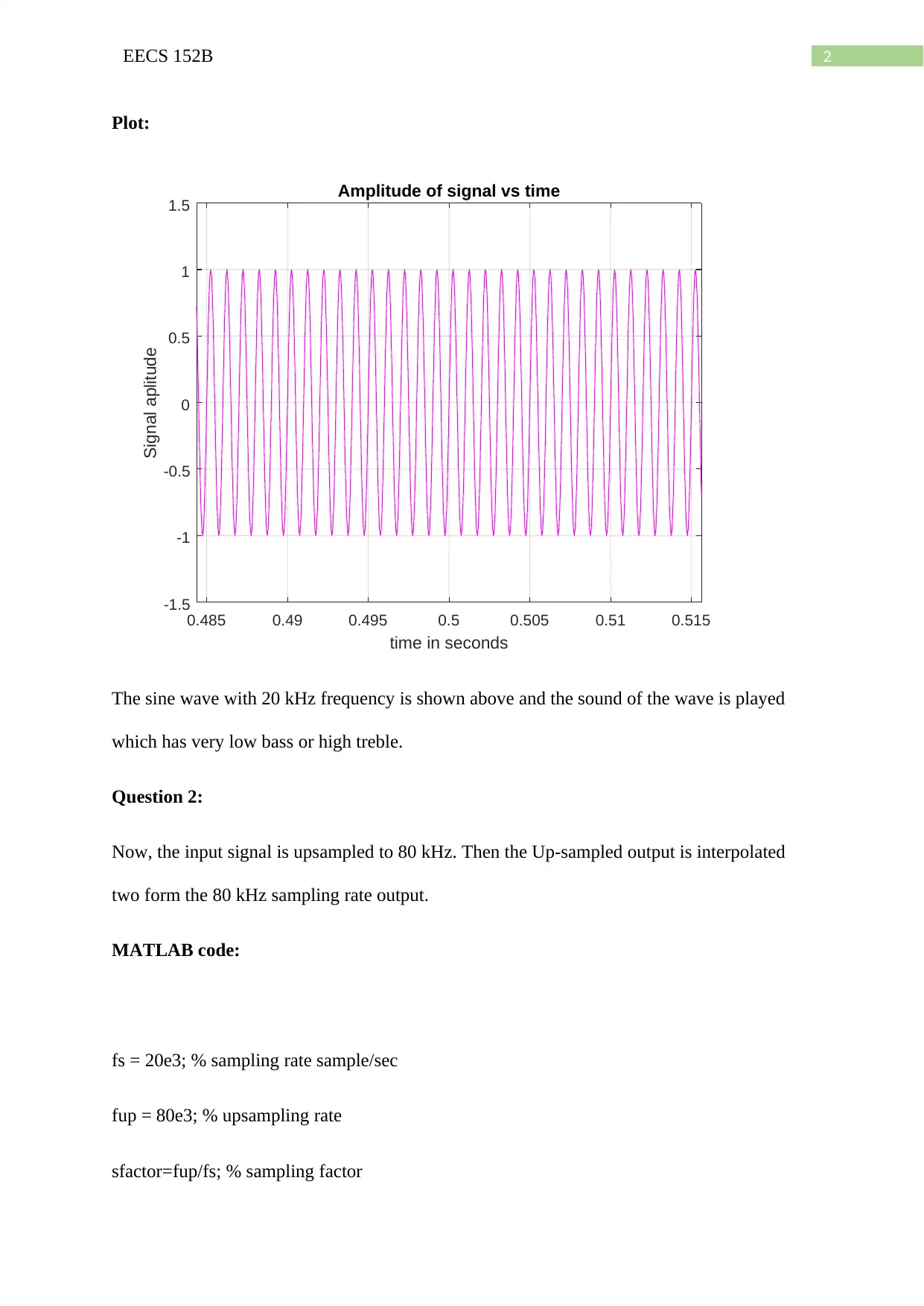
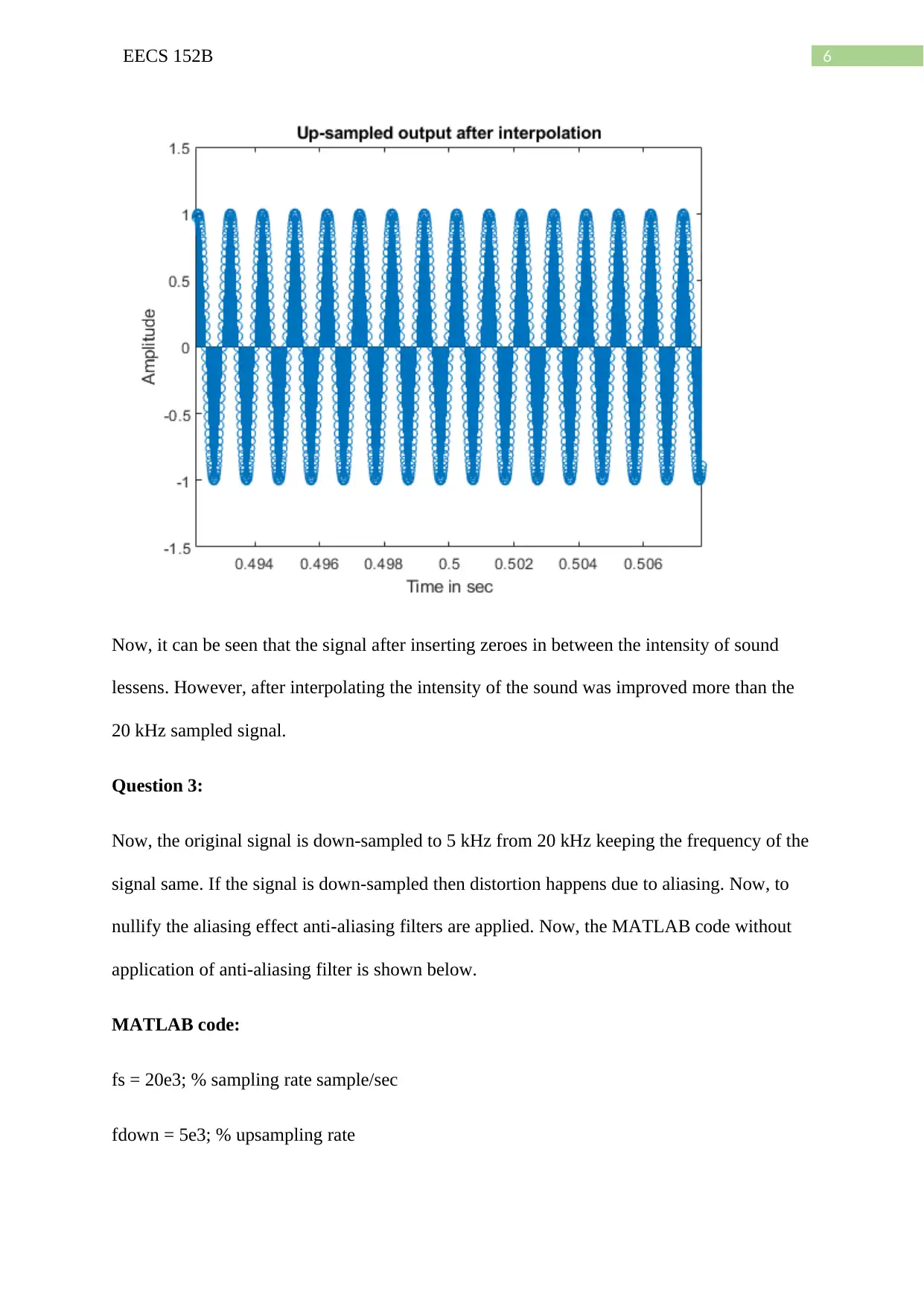
This assignment solution for EECS 152B, focuses on sample rate conversion techniques using MATLAB. It begins by generating and analyzing a 1000 Hz sine wave sampled at 20 kHz, playing the sound, and observing the effect. The solution then addresses upsampling to 80 kHz, exploring zero insertion and interpolation, and comparing the sound before and after each process. Next, the assignment investigates downsampling to 5 kHz and the necessity of anti-aliasing filters to mitigate aliasing effects. Further, the solution examines downsampling by a factor of 12 and its impact on signal intensity. Finally, it uses the 'tchaikovsky.mat' file to explore downsampling with factors 5/6 and 2/3, applying low-pass filters, and then downsampling with factors 1/2, 1/3 and 1/6. The solution also covers upsampling with factors 3/2, 9/2, and 21/2, applying low-pass filters and linear interpolator filters to remove aliasing effects and comparing the outcomes. The assignment demonstrates the effects of different rate conversion techniques on signal quality and the importance of filtering.

Running head: EECS 152B
EECS 152B
Name of the Student
Name of the University
Author Note

1EECS 152B
Question 1:
The MATLAB code for generating samples of a sin wave having frequency 1000 Hz which is
sampled by rate 20 kHz is given below. Then the sound command is used to listen the signal
as sound wave.
MATLAB code:
fs = 20e3; % sampling rate sample/sec
delt = 1/fs; % time increment sec/sample
t = 0:delt:1;
f = 1e3; % frequency of signal
s = sin(2*pi*f*t); % signal amplitude is 1
plot(t,s,'m')
xlabel('time in seconds');
ylabel('Signal aplitude');
title('Amplitude of signal vs time')
grid on
zoom(32)
ylim([-1.5,1.5])
sound(s,fs)

2EECS 152B
Plot:
0.485 0.49 0.495 0.5 0.505 0.51 0.515
time in seconds
-1.5
-1
-0.5
0
0.5
1
1.5
Signal aplitude
Amplitude of signal vs time
The sine wave with 20 kHz frequency is shown above and the sound of the wave is played
which has very low bass or high treble.
Question 2:
Now, the input signal is upsampled to 80 kHz. Then the Up-sampled output is interpolated
two form the 80 kHz sampling rate output.
MATLAB code:
fs = 20e3; % sampling rate sample/sec
fup = 80e3; % upsampling rate
sfactor=fup/fs; % sampling factor

3EECS 152B
delt = 1/fs; % time increment sec/sample
t = 0:delt:1;
f = 1e3; % frequency of signal
s = sin(2*pi*f*t); % signal amplitude is 1
figure(1)
subplot(2,1,1)
stem(t,s)
xlabel('Time in sec');
ylabel('Amplitude');
title('Signal output before Up-sampling');
zoom(64)
ylim([-1.5,1.5])
%%% zero insertion
lx = length(s);
y = 0;
y(1) = s(1);
for i=2:lx
c = [zeros(1,sfactor-1),s(i)];
y = [y,c];

4EECS 152B
end
%%% Output display of zeros inserted signal
nm=linspace(0,1,length(y));
figure(1)
subplot(2,1,2)
stem(nm,y); %Upsampled version of signal
xlabel('Time in sec');
ylabel('Amplitude');
title('Zeros inserted Output of Signal');
zoom(64)
ylim([-1.5,1.5])
sound(y,fup)
xi=s;
yi = interp(xi,sfactor);
nn=linspace(0,1,length(yi));
figure(2)
stem(nn,yi); %interpolation output
xlabel('Time in sec');
ylabel('Amplitude');

5EECS 152B
title('Up-sampled output after interpolation');
zoom(64)
ylim([-1.5,1.5])
sound(yi,fup)
Plots:

6EECS 152B
Now, it can be seen that the signal after inserting zeroes in between the intensity of sound
lessens. However, after interpolating the intensity of the sound was improved more than the
20 kHz sampled signal.
Question 3:
Now, the original signal is down-sampled to 5 kHz from 20 kHz keeping the frequency of the
signal same. If the signal is down-sampled then distortion happens due to aliasing. Now, to
nullify the aliasing effect anti-aliasing filters are applied. Now, the MATLAB code without
application of anti-aliasing filter is shown below.
MATLAB code:
fs = 20e3; % sampling rate sample/sec
fdown = 5e3; % upsampling rate

7EECS 152B
sfactor=fs/fdown; % down-sampling factor
delt = 1/fs; % time increment sec/sample
t = 0:delt:1;
f = 1e3; % frequency of signal
s = sin(2*pi*f*t); % signal amplitude is 1
figure(1)
subplot(2,1,1)
stem(t,s)
xlabel('Time in sec');
ylabel('Amplitude');
title('Signal output before Up-sampling');
zoom(64)
ylim([-1.5,1.5])
sdown = [];
for i=1:sfactor:length(s)
sdown = [sdown s(i)];
end
time = linspace(0,1,length(sdown));
figure(1)
subplot(2,1,2)

8EECS 152B
stem(time,sdown)
xlabel('Time in sec');
ylabel('Amplitude');
title('Signal output after down-sampling');
zoom(64)
ylim([-1.5,1.5])
Output:
-1
0
1
Amplitude
Signal output before Up-sampling
0.494 0.496 0.498 0.5 0.502 0.504 0.506
Time in sec
-1
0
1
Amplitude
Signal output after down-sampling
0.494 0.496 0.498 0.5 0.502 0.504 0.506
Time in sec
Question 4:
If one of every 12 samples are kept of the original sine wave or down-sampling the sine wave
by a factor 12, then the intensity of the sine wave will be reduced 12 times. Now, the down-
sampled signal is produced in MATLAB.

9EECS 152B
MATLAB function:
fs = 20e3; % sampling rate sample/sec
sfactor=12; % down-sampling factor
fdown = fs/12; % down-sampled rate
delt = 1/fs; % time increment sec/sample
t = 0:delt:1;
f = 1e3; % frequency of signal
s = sin(2*pi*f*t); % signal amplitude is 1
sound(s,fs)
figure(1)
subplot(2,1,1)
stem(t,s)
xlabel('Time in sec');
ylabel('Amplitude');
title('Signal output before Up-sampling');
zoom(64)
ylim([-1.5,1.5])
sdown = [];
for i=1:sfactor:length(s)
sdown = [sdown s(i)];

10EECS 152B
end
time = linspace(0,1,length(sdown));
figure(1)
subplot(2,1,2)
stem(time,sdown)
xlabel('Time in sec');
ylabel('Amplitude');
title('Signal output after down-sampling');
zoom(64)
ylim([-1.5,1.5])
sound(sdown,fdown)
Plot:

11EECS 152B
-1
0
1
Amplitude
Signal output before down-sampling
0.494 0.496 0.498 0.5 0.502 0.504 0.506
Time in sec
-1
0
1
Amplitude
Signal output after down-sampling
0.494 0.496 0.498 0.5 0.502 0.504 0.506
Time in sec
Now, after playing the original signal and the down-sampled signal it is clear that the
intensity of the sound of the signal has been reduced after down-sampling by a factor 12.
Question 5:
In this question tchaikovsky.mat is needed as source signal and then up-sampling and down-
sampling methods can be applied.
a) Now, first the signal is down-sampled by factor 5/6 and 2/3. A low pass filter is applied
with pass-band frequency assumed as 100 Hz and the sample rate = 44.1*(5/6) Hz.
MATLAB code:
load('tchaikovsky.mat')
s = sugar_plum;
sdown5by6 = s;