Solved Physics Assignment: Electric & Magnetic Fields & Gauss Law

This document presents detailed solutions to various physics problems centered on electric and magnetic fields, along with applications of Gauss's law. The solutions cover scenarios involving calculating magnetic field contributions from current-carrying wires, determining electric fields due to charge distributions along arcs, and applying Gauss's law to find electric fields within and outside charged spheres and cylindrical shells. Each problem includes step-by-step derivations, integrations, and explanations to illustrate the underlying principles and methodologies. The solutions demonstrate the application of fundamental physics concepts to solve complex electromagnetic problems. Desklib offers a wealth of similar solved assignments and past papers to aid students in their studies.

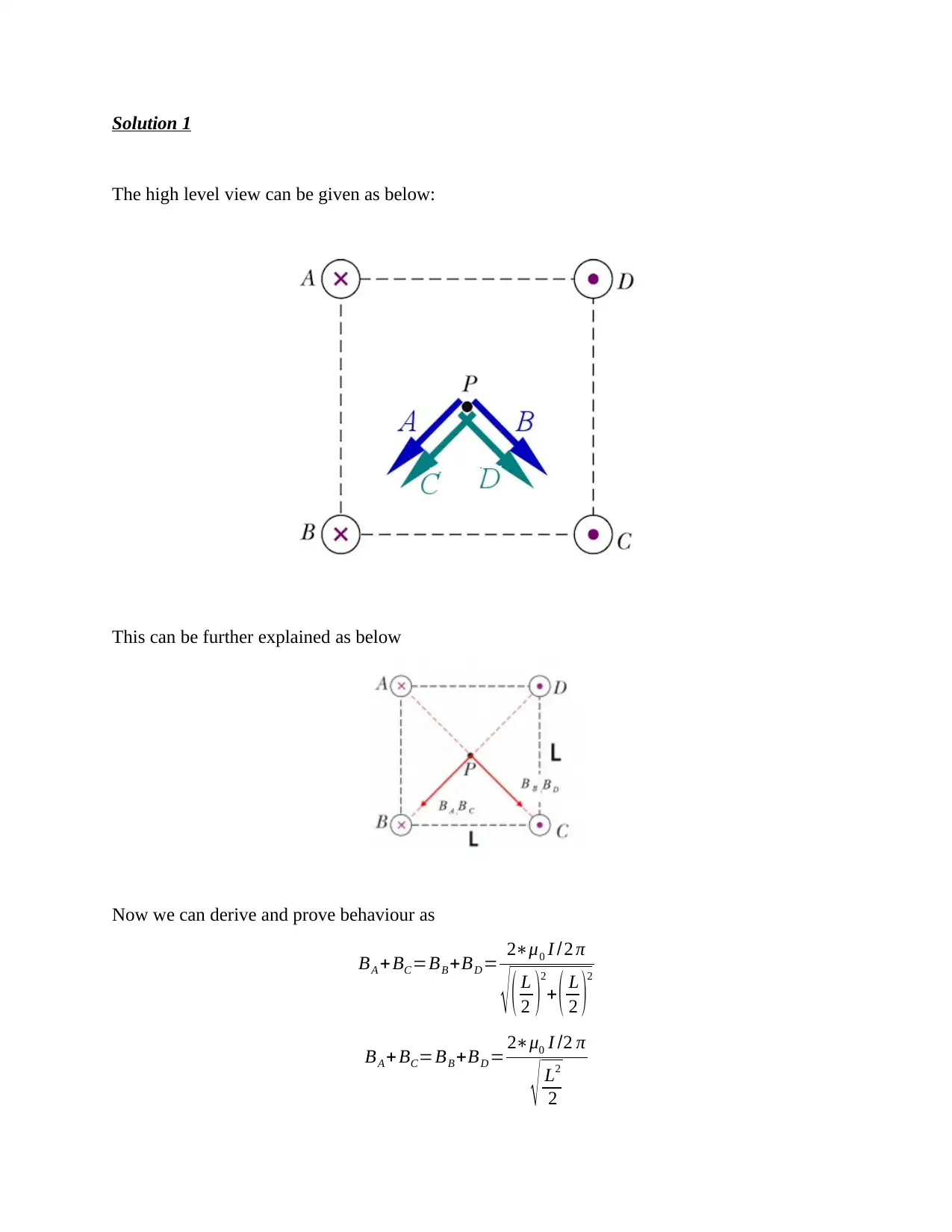
Solution 1
The high level view can be given as below:
This can be further explained as below
Now we can derive and prove behaviour as
BA + BC=BB +BD = 2∗μ0 I / 2 π
√ ( L
2 )2
+ ( L
2 )2
BA + BC=BB +BD = 2∗μ0 I /2 π
√ L2
2

BA + BC=BB +BD = μ0 I
πL √ 1
2
BA +BC=BB +BD = μ0 I √2
πL
The direction is downwards
Solution 6
a)
Expression of electric field is
dE=k dQ
r2
Part 1: from (-r to 0)
Assuming θ is the angle with x axis then we can have
d Ex=dE cos ( θ )
d Ey=dE sin ( θ )

Integrating this we can have
Ex=∫
❑
❑
k dQ
r2 cos ( θ )
Ex=∫
π
π /2
k dQ
r2 cos ( θ )
Ex=∫
π
π /2
k λr∗dθ
r2 cos ( θ )
Ex= λk
r
Similarly
E y=∫
❑
❑
k dQ
r2 sin ( θ )
E y=∫
π
π / 2
k dQ
r2 sin ( θ )
E y=∫
π
π / 2
k λr∗dθ
r2 sin ( θ )
E y=− λk
r
Now
λ= q
π
2 ∗r
λ= 2q
πr
Hence
Ex= λk
r =
2 q
πr k
r = 2qk
π r2

E y=− λk
r =−2 qk
π r2
Part 2: from (0 to r)
Assuming θ is the angle with x axis then we can have
d Ex=dE cos ( θ )
d Ey=dE sin ( θ )
Integrating this we can have
Ex=∫
❑
❑
k dQ
r2 cos ( θ )
Ex=∫
π /2
0
k dQ
r2 cos ( θ )
Ex=∫
π /2
0
k λr∗dθ
r2 cos ( θ )
Ex=−λk
r
Similarly
E y=∫
❑
❑
k dQ
r2 sin ( θ )
E y=∫
π / 2
0
k dQ
r2 sin ( θ )
E y=∫
π / 2
0
k λr∗dθ
r2 sin ( θ )
E y=− λk
r
Now

λ= −q
π
2 ∗r
λ=−2 q
πr
Hence
Ex=−λk
r =
−2 q
πr k
r = 2 qk
π r2
E y=− λk
r =+2 qk
π r2
b)
Expression of electric field is
dE=k dQ
r2
Part 1: from (-r to 0)
Assuming θ is the angle with x axis then we can have
d Ex=dE cos ( θ )
d Ey=dE sin ( θ )
Integrating this we can have

Ex=∫
❑
❑
k dQ
r2 cos ( θ )
Ex=∫
π
π /2
k dQ
r2 cos ( θ )
Ex=∫
π
π /2
k λr∗dθ
r2 cos ( θ )
Ex= λk
r
Similarly
E y=∫
❑
❑
k dQ
r2 sin ( θ )
E y=∫
π
π / 2
k dQ
r2 sin ( θ )
E y=∫
π
π / 2
k λr∗dθ
r2 sin ( θ )
E y=− λk
r
Now
λ= 2 q
π
2 ∗r
λ= 4 q
πr
Hence
Ex= λk
r =
4 q
πr k
r = 4 qk
π r2
E y=− λk
r =−4 qk
π r2

Part 2: from (0 to r)
Assuming θ is the angle with x axis then we can have
d Ex=dE cos ( θ )
d Ey=dE sin ( θ )
Integrating this we can have
Ex=∫
❑
❑
k dQ
r2 cos ( θ )
Ex=∫
π /2
0
k dQ
r2 cos (θ )
Ex=∫
π /2
0
k λr∗dθ
r2 cos (θ )
Ex=−λk
r
Similarly
E y=∫
❑
❑
k dQ
r2 sin ( θ )
E y=∫
π / 2
0
k dQ
r2 sin ( θ )
E y=∫
π / 2
0
k λr∗dθ
r2 sin ( θ )
E y=− λk
r
Now

λ= −q
π
2 ∗r
λ=−2 q
πr
Hence
Ex=−λk
r =
−2 q
πr k
r = 2 qk
π r2
E y=− λk
r =+2 qk
π r2
Solution 7
(a) Express the charge dq in a
shell of thickness drand volume
4r2dr:
dq=4 πr2 ρdr =4 πr2 ( Ar ) dr
¿ 4 π Ar3 dr
Integrate this expression from
r = 0 to R to find the total charge
on the sphere:
Q=4 πA∫
0
R
r3 dr = [ π Ar4 ] 0
R
=π AR4

(b) Use Gauss’s law to find the
electric field in the region r <R1: ∮S En dA= 1
∈0
Qinside
and
Er< R1= Qinside
∈0 A =0
because Qinside = 0.
Apply Gauss’s law in the region
R1<r <R2:
ER1<r< R1
= q1
∈0 ( 4 πr2 ) = kq1
r2
Using Gauss’s law, find the
electric field in the region r>R2: Er> R2
= q1 + q2
∈0 ( 4 πr2 ) = k ( q1 + q2 )
r2
(c) Set Er> R2
=0 to obtain: q1 +q2=0
or
q1
q2
=−1
The electric field lines for the
situation in (b) with q1 positive is
shown to the right.
d)

(b) Apply Gauss’s law to a
spherical surface of radius r>R
that is concentric with the
nonconducting sphere to obtain:
∮S Er dA= 1
∈0
Q inside
or
4 πr2 Er=Qinside
∈0
Solve for Er: Er ( r >R ) =Qinside
4 π ∈0
1
r2 =kQinside
r2
¿ kA πR4
r2 = AR4
4 ∈0 r2
Apply Gauss’s law to a spherical
surface of radius r<R that is
concentric with the
nonconducting sphere to obtain:
∮S Er dA= 1
∈0
Q inside
or
4 πr2 Er=Qinside
∈0
Solve for Er: Er ( r < R ) = Qinside
4 πr2 ∈0
= π Ar4
4 πr2 ∈0
= Ar2
4 ∈0
e)
(b) Apply Gauss’s law to a
spherical surface of radius r>R
that is concentric with the
nonconducting sphere to obtain:
∮S Er dA= 1
∈0
Q inside
or
4 πr2 Er=Qinside
∈0

Solve for Er: Er ( r >R ) =Qinside
4 π ∈0
1
r2 =kQinside
r2
¿ kA πR4
r2 = AR4
4 ∈0 r2
Apply Gauss’s law to a spherical
surface of radius r<R that is
concentric with the
nonconducting sphere to obtain:
∮S Er dA= 1
∈0
Qinside
or
4 πr2 Er=Qinside
∈0
Solve for Er: Er ( r < R ) = Qinside
4 πr2 ∈0
= π Ar4
4 πr2 ∈0
= Ar2
4 ∈0
f)
Express Qinside for r>b: Qinside=ρV = ρπ b2 L−ρπ a2 L
¿ ρπ L ( b2−a2 )
Substitute for Qinside to obtain: En ( r > b ) = ρπ L ( b2−a2 )
2 π ∈0 rL
¿ ρ ( b2−a2 )
2∈0 r
(g)

Express the charge dq in a shell
of thickness drand volume
4r2dr:
dq=4 πr2 ρdr =4 πr2 ( Ar ) dr
¿ 4 π Ar3 dr
Integrate this expression from
r = 0 to R to find the total charge
on the sphere:
Q=4 πA∫
0
R
r3 dr = [ π Ar4 ] 0
R
=π AR4
The graph of Er versus r/R, with Er in units of A/4
0, was plotted using a
spreadsheet program.