Circuit Theory Solutions: Electrical and Electronic Principles

This assignment solution covers various aspects of circuit theory within the context of electrical and electronic principles. It includes problems related to Thevenin's theorem, Kirchhoff's Current Law (KCL), Kirchhoff's Voltage Law (KVL), source transformation, Y-Δ transformations, power calculations, and transformer regulation. The solutions demonstrate step-by-step calculations and explanations for each problem, providing a comprehensive understanding of the underlying concepts. Topics covered are calculating Thevenin equivalents, applying KCL and KVL to solve complex circuits, converting between Y and Δ configurations, computing power in AC circuits, and determining voltage regulation in transformers. Desklib offers this document as part of its collection of solved assignments and study resources for students.

MODULE TITLE : ELECTRICAL AND ELECTRONIC PRINCIPLES
TOPIC TITLE : CIRCUIT THEORY
TUTOR MARKED ASSIGNMENT 1 (v3.1)
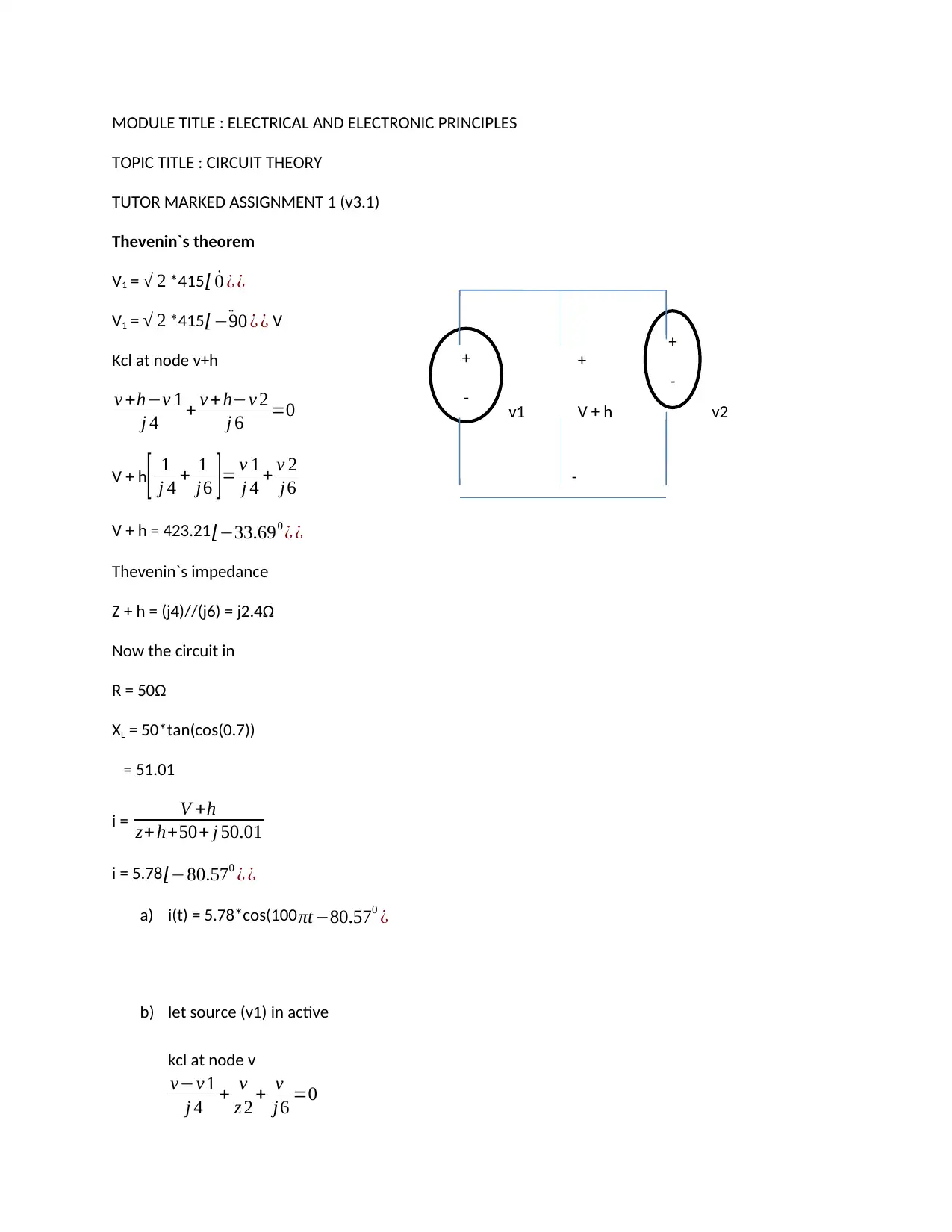
Thevenin`s theorem
V1 = √ 2 *415⌊ ˙0 ¿ ¿
V1 = √ 2 *415 ⌊ ¨−90 ¿ ¿ V
Kcl at node v+h +
v +h−v 1
j 4 + v +h−v 2
j 6 =0 v1 V + h v2
V + h[ 1
j 4 + 1
j6 ] = v 1
j 4 + v 2
j6 -
V + h = 423.21⌊−33.690 ¿ ¿
Thevenin`s impedance
Z + h = (j4)//(j6) = j2.4Ω
Now the circuit in
R = 50Ω
XL = 50*tan(cos(0.7))
= 51.01
i = V +h
z+ h+50+ j 50.01
i = 5.78 ⌊−80.570 ¿ ¿
a) i(t) = 5.78*cos(100πt −80.570 ¿
b) let source (v1) in active
kcl at node v
v−v 1
j 4 + v
z 2 + v
j6 =0
+
-
+
-

v [ 1
j 4 + 1
50+ j51.01 + 1
j6 ] = √ 2∗415
j 4
V =343.79 ⌊−1.3150¿ ¿V
i1= v
z 2 = v
50+ j50.01 =4.813 ⌊−46.86 ¿ ¿ A
let source v 2∈active
Kcl at node v
V
j 4 + V
z 2 + V −V 2
j 6 = 0
v [ 1
j 4 + 1
50+ j 51.01 + 1
j6 ] =√ 2∗415 ⌊−900 ¿ ¿
V =229.15 ⌊−9.130 ¿ ¿
i2 = V
z 2 =3.208 ⌊−136.880 ¿ ¿
i = i1 + i2 = 5.78 ⌊−80.570 ¿ ¿
i(t) = 5.78*cos(100πt −80.570 ¿ A
c) By source transformation
I1 = V 1
j 4 =146.72 ⌊−900 ¿ ¿
I2 = V 2
j 6 =97.82 ⌊ 1800 ¿¿
I = I1 + I2
I = 176.33 ⌊−123.690 ¿ ¿
(j4)//(j6) = j2.4
Now the circuit is
By current division rule
i = 176.33 ⌊−123.690 ¿ ¿
i = 5.78 ⌊−80.570 ¿ ¿ A
i(t) = 5.78*(100 πt −80.570 ¿ A

Q2a)
Apply KVL in loop 1
-v1 + I1Z1 +(I1 – I2)Z4 = 0
120 + 2I1 – j5(I1-I2) = 0
(2 – j5)I1 + j5I2 = 120 ….1
Apply KVL in loop 2
(I2 – I1)Z4 + (I2 – I4)Z2 + (I2 – I3)Z3 = 0
J5I1 – j6I2 – j4I3 + j5I4 = 0
5I1 – 6I2 – 4I3 + 5I4 = 0 ………….2
Applying KVL in loop 3
(I3 – I2)Z5 + I3Z3 + V2 = 0
(I3 – I2)(j4) + I3(4) + 120<900 = 0
-j4I2 + (4 + j4)I3 = -j120 ………………3
Apply KVL in loop 4
-V3 + (I4 – I2)Z2 = 0
20<450 + (I4 – I2)(-j5) = 0
-j5I2 + j5I4 = 10√2+ j 10 √2 …………….4
Solve equation 1,2,3 and 4

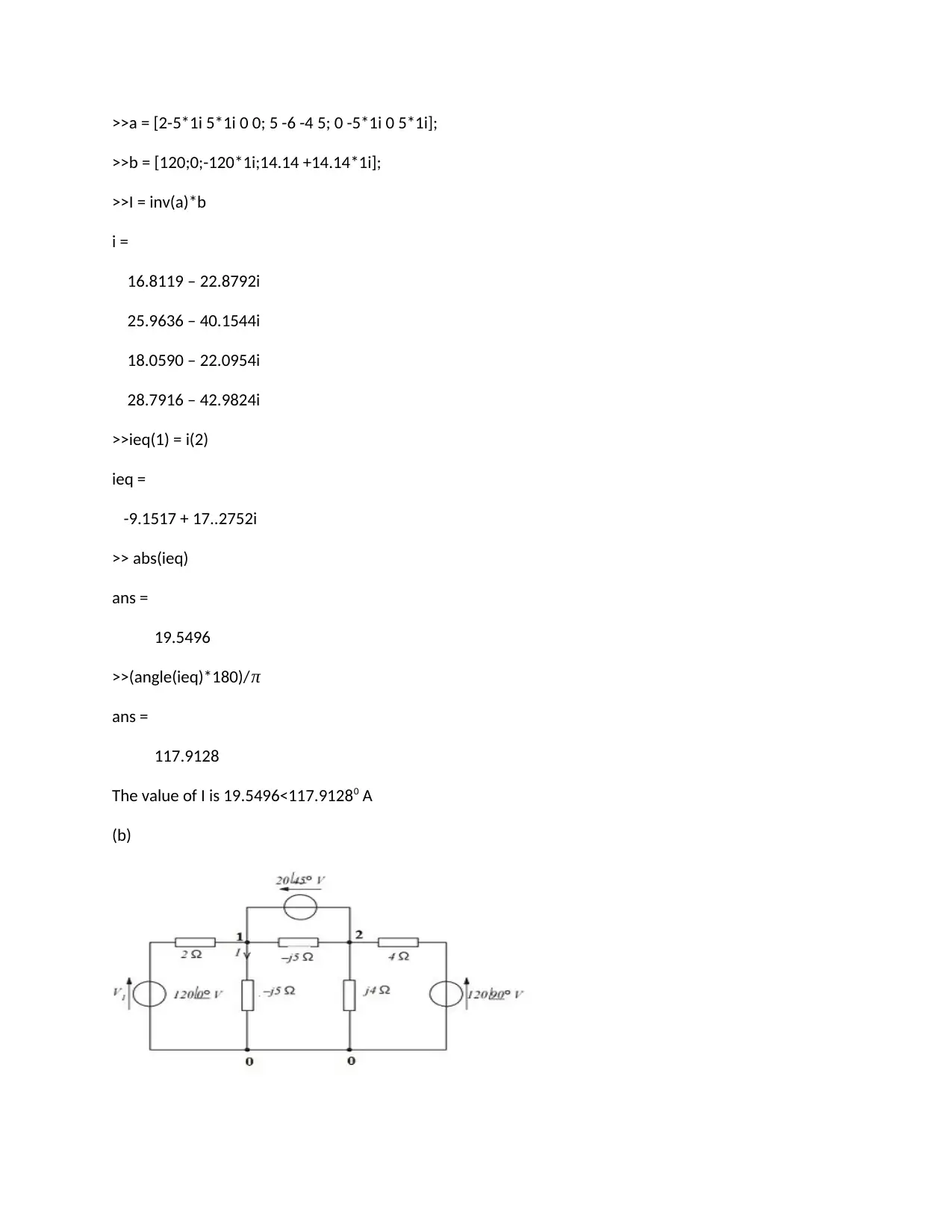
>>a = [2-5*1i 5*1i 0 0; 5 -6 -4 5; 0 -5*1i 0 5*1i];
>>b = [120;0;-120*1i;14.14 +14.14*1i];
>>I = inv(a)*b
i =
16.8119 – 22.8792i
25.9636 – 40.1544i
18.0590 – 22.0954i
28.7916 – 42.9824i
>>ieq(1) = i(2)
ieq =
-9.1517 + 17..2752i
>> abs(ieq)
ans =
19.5496
>>(angle(ieq)*180)/π
ans =
117.9128
The value of I is 19.5496<117.91280 A
(b)

The only principle nodes in the circuit are 1 and 2 and they form super node
Apply KCL at super node
V 1−120
2 + V 1
− j5 + V 1−V 2
− j5 + V 2−V 1
− j5 + V 2
J 4 + V 2−120<900
4 =0
V1(0.5 + j0.2) + (-j0.25+0.25)V2 = 60 + j30 …..(1)
Apply KVL across the super node
-V1 + 20<450 + V2 = 0
V1 – V2 = 14.14 +j14.14 …………2
Solve equations 1 and 2
>> x = [0.5 + 1i *0.2 0.25 – 1i *0.25; 1-1];
>> y = [60 + 30*1i; 14.14 + 1i * 14.14];
>> v = inv(x) *y;
>> ieq = v(i)/(-5*1i);
>> abs(ieq)
ans =
19.5496
>>(angle(ieq)*180)/π
ans =
117.9128
The value of I is 19.5496<117.91280 A
Q3a) Given
Zy = (15 +j15) Ω
ZA = (45 + j45) Ω
Finding a single equivalent ∆ connected load
Converting star connected load to ∆ connected and then solve two possible ∆ connected loads
ZY - ∆ = ZY *3 = (15 + j15) *3

= (45 + j45) Ω
Now they become parallel
So
Zequivalent (∆) = Z ( Y −∆ )∗Z ∆
Z ( Y −∆ ) +Z ∆
= ( 45+ j 45 )∗(45+ j 45)
90+ j 90
Solving we get
Zeq - ∆ = 22.5 + j22.5 Ω
b) Finding Y – connected load equivalent
so
Zeqv(Y) = Zeq (∆)
3
= 22.5+22.5 j
3
= 7.5 + 7.5j Ω
(c )= converting ∆ load to star load
Zeqv(Y) = Zeq (∆)
3
= 45+ 45 j
3
= 15 + 15j Ω
The two Y – connected load become parallel to each other. So equivalent load is
Zeq = ( 15+15 j )∗(15+15 j)
30+ 30 j
= (7.5 + 7.5j ) Ω

d) The total power
V = 415 V
f = 50 Hz
Power = Re[3*VI*]
I => phase current
So,
I = V
Zeq (∆)= 415
22.5+22.5 j
= 415 ⌊ 00 ¿ ¿ ¿ = 13.04 ⌊−450 ¿ ¿
So
Power = Re(3*415 ⌊ 00 ¿ ¿
= Re[16234.8cos450 + 16234.8sin450]
= Re(11481.5 + 11481.5j
= 11481.5 W
Q4)
a) Applying KVL to loop 1 in fig a , that is abef
ABEF: V = jwA*L1 * I1+jw *M *I2
ABCDEF: V = jw*L2 *I2 + jw*M*I1
b) I1 = (V*(L2 –m))/jw(L1*L2-m2)) …..1
I2 = (V*(L1 –m))/jw(L1*L2-m2)) …..2
By dividing the equation1/equation 2 we get
I 1
I 2 =¿ (V*(L2 – m)/(jw*(L1*L2-m2)/(V*(L1-m))/(jw*(L1*L2-m2)
I 1
I 2 = L 2−M
L 1−M
c) Leq = I1 + I2 => V ∗(L 2−m)
jw∗( L1∗L2−m2) + V∗( L1−m)
jw∗(L1∗L2−m2 )
= V ∗(L1+L 2−2 M )
jw∗(L1−L2−M2)
= V
jw∗Leq
d) Since current is at zero admittance, and L1 = L2 = L
1
2 π √Lc =fv
¿ 1
2 π √L 1∗10−9
= 1000000 => L = 25.33 μH

L = 25.33 μH
Q5)
Primary winding voltage V1 = 415 V
Secondary winding voltage V2 = 11k
Rating of transformer = 200 kVA
Winding resistance referred to primary R1eq = 0.014Ω
Winding leakage reactance referred to primary X1eq = 0.057Ω
a) % regulation of transformer at 0.8 power factor lagging
Primary winding current, I1 = 200
415 = 482 A
Power factor cosθ = 0.8
sin θ=0.6
%voltage regulation = I 1∗R 1 eq
V 1 ∗cosθ+ I 1∗R 1 eq
V 1 ∗sinθ
= 482∗0.014
415 ∗0.8+ 482∗0.057
415 ∗0.6
= 0.013 + 0.03972
= 0.05272
= 5.272%
b) Primary winding resistance R1 = 10mΩ = 0.01Ω
% voltage regulation = 2% = 0.02
Power factor =
cos θ=1
sin θ=0
% voltage regulation = I 1∗R 1 eq
V 1 ∗cosθ+ I 1∗X 1eq
V 1 ∗sinθ
0.02 = 482∗R 1 eq
415 ∗1+ 482∗X 1 eq
415 ∗0
R1 eq = 0.0172 Ω
R1 eq = R1 + R 2
K2

Where k is transformation ratio
K = N 2
N 1 = V 2
V 1 =11000
415 =26.5
0.0172 = 0.01 + R 2
26.52
R2 = 5.0585 Ω
Maximum secondary winding resistance R2 = 5.0585 Ω