EE Assignment: Circuit Analysis, Calculus, and Amplifier Design

This document provides a detailed solution to an Electrical Engineering assignment. The assignment covers a wide range of topics including circuit analysis, calculus, and amplifier design. The solution begins with calculations of currents, voltages, and power in various circuits, applying Ohm's law and circuit analysis techniques. It then delves into resonance, calculating frequency, Q factor, and circuit current. Further, the assignment investigates AC circuits, calculating impedance, current, and power factor. Additionally, it covers amplifier analysis, calculating voltage and current gains, and overall power gain. The solution also includes analysis of thermocouples and analog-to-digital converters. Finally, it explores control systems, including damping and transfer functions, as well as calculus problems involving derivatives and integrals. The assignment concludes with a bibliography of relevant sources.

QUESTIONS SOLUTIONS
Student Name
Institution Affiliation
Instructor’s Name
Date

Task 1
A R1 100 B Rꭥ 2 170ꭥ C
V115V RL 220ꭥ V2 12V
F E D
a. The currents flowing through R1 and R2
V=IR
For Loop 1
V=I1R1 + I2R2
15=100I1 + 250I2
Loop 2
12V=I3R3 + I1R1
=170I3 + 250I2
Loop 3
15V-12V=100I1 – 170I2
Equation 1
15V=100I1 + 250(I1+I3)
15V =350I1 + 250I3
Equation 2
12V=170I3 + 250(I1+I3)
12V=420I3 + 250I1
15V=(250I3 + 350I1)*5
12V=(420I3 + 250I1)*7 You multiply by 5 and 7 to equalize I1 in both equations
After multiplying you get
75V=1250I3 +1750I1
84V= 2940I3 +1750I1
-9V=-1690I3
I3=-9¿1690
I3=5.3mA
I1=84V=2940(0.0053) + 1750I1

84-15.582 = 1750I1
68.418=1750I1
I1= 68.418
1750
I1=39mA
b. The current through RL
IL=I3 +I1
=5.3mA + 39mA
=44.3mA
c. The p.d developed across RL
V=IR
=44.3mA * 220
=0.0443*220
=9.746V
d. The power dissipated by RL
P=VI
=9.746*0.0443
=0.4317478 W

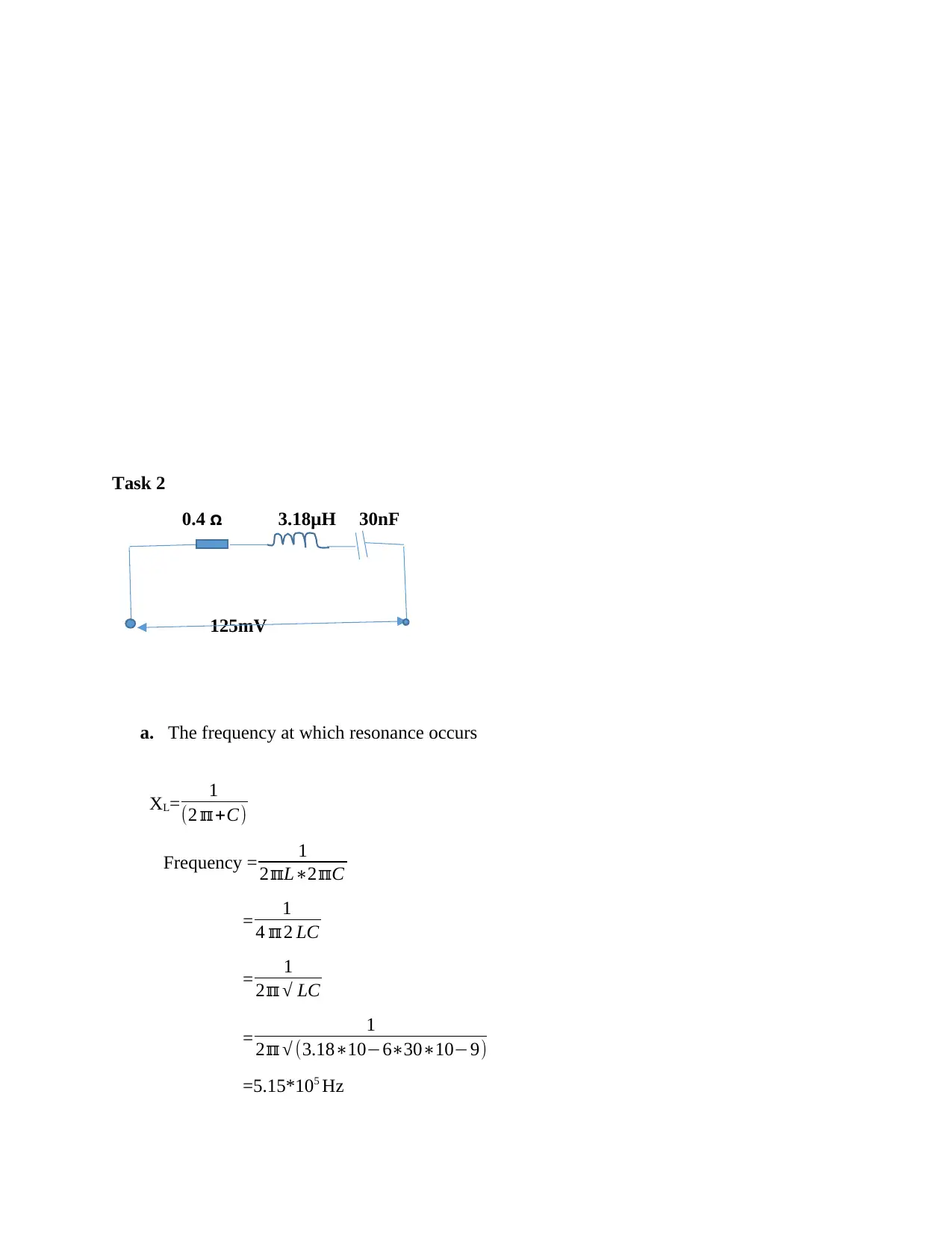
Task 2
0.4 3.18μH 30nFꭥ
125mV
a. The frequency at which resonance occurs
XL= 1
(2 ℼ+C)
Frequency = 1
2 Lℼ ∗2 Cℼ
= 1
4 ℼ2 LC
= 1
2ℼ √ LC
= 1
2ℼ √ (3.18∗10−6∗30∗10−9)
=5.15*105 Hz

b. The circuit Q factor
w= 1
√ (LC)
Q= X L
R
= 2ℼ+ L
0.4
= 2 fℼ 3.18∗10−6
0.4
=25.72
c. The capacitor p.d at resonance
XC= 1
2ℼ+C
= 1
2ℼ∗f∗30∗10−9
Vc=Im * Xc
Im at resonance = 125∗10−3
0.4
p.d=Im * Xc
= 125∗10−3
0.4 * 1
2ℼ∗f ∗30∗10−9
=0.0303
d. The circuit current
I= V
R
= 125∗10−3 V
0.4
=0.3125A
e. The bandwidth of the current
Bandwidth=frequency/Q

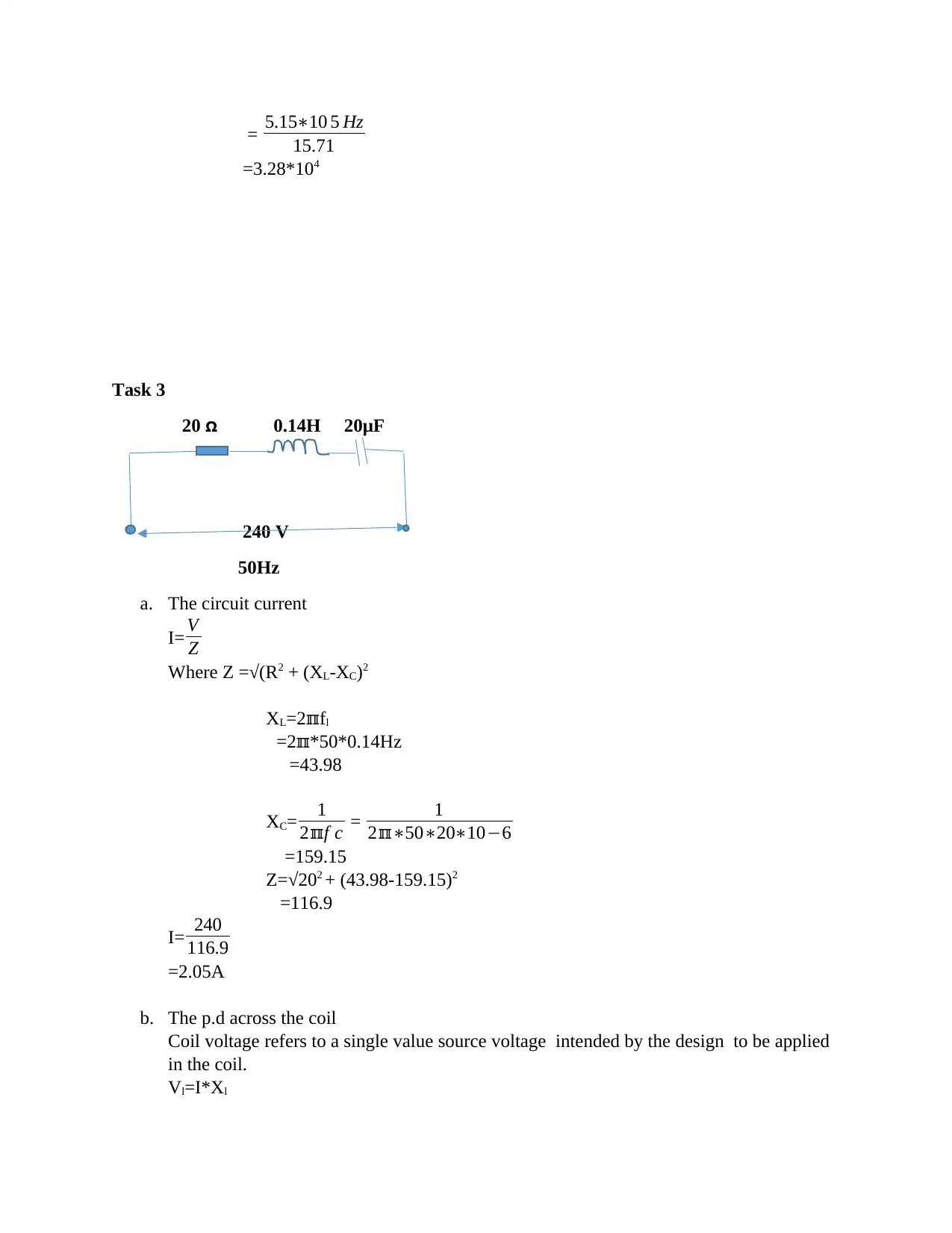
= 5.15∗10 5 Hz
15.71
=3.28*104
Task 3
20 0.14H 20μFꭥ
240 V
50Hz
a. The circuit current
I= V
Z
Where Z =√(R2 + (XL-XC)2
XL=2 fℼ l
=2 *50*0.14Hzℼ
=43.98
XC= 1
2 fℼ c = 1
2ℼ∗50∗20∗10−6
=159.15
Z=√202 + (43.98-159.15)2
=116.9
I= 240
116.9
=2.05A
b. The p.d across the coil
Coil voltage refers to a single value source voltage intended by the design to be applied
in the coil.
Vl=I*Xl

=2.05*43.98
=90.159V
c. The p.d across the capacitor
Vc=I*Xc
=2.05*116.9
=240V
d. The phase angle
Cosα= R
Z
= 20
116.9
=0.171
α=80.15
e. The power factor of the circuit
The power factor refers to the cosine of phase angle
=cos 80.15
=0.171
Task 4
a. The circuit current
I= V
Z
Z= √(R2 + XL2)
XL=2 *50*250*10ℼ -6
=0.07854
Therefore Z=√1225 + 6.168*10-3
=35
I= 240
35
=6.857
b. The power factor
The power factor is the ratio of the actual electrical power dissipated by an AC
circuit to the product of the r.m.s. values of current and voltage. The difference

between the two elements is caused by reactance in the circuit and represents the
power that does no useful work.
Cos α= R
Z
= 35
35
=1
α = 0
c. The power supplied by the power supply
=240V
d. The power dissipated by the circuit
=VR + VL
IR + IXL
6.857*35 + 6.857*0.07854
=240.5W
e. The power factor correction capacitor needed to increase the power factor to 0.95
Task 5
a. The voltage gain in amplifier 1 in dB form
Voltage Gain(A1)= Output V
Input V
= 4000
12
In dB= 20 log 4000
12

b. The current gain in amplifier 1 in dB form
Current gain=)= Output I
Input I
= 350
3
In dB =20 log 350
3
c. The output voltage of Amlifier 2
=33= V
4
=V= 33*4
=132
d. Ai= I out
I ∈¿ ¿
Vout=Ailog 22* 350 mA
20
e. Overall power gain
Power gain = Output power
Input power 3
=current gain * voltage gain
= 4000
12 * 350
3
=38.89 MW
Task 6
a. The maximum voltage output of a thermocouple
=0.5mV=1oC
? =450oC
(0.5*450)mV
=225mV
b. The gain of the signal conditioning the amplifier
= Output V
Input V
= 4.5
0.225

=20
In dB =20 log 20
c. The number of bits of analogue to digital converter
=V ∈ ¿
V ref ¿ x 256
= 4.5
7.5∗10−4 *256
=1.536*106 bits
d. The output from a thermocouple for a temperature of 285oC
= 0.5 mV
oC
=0.5mV=1oC
? =285 oC
0.5*285
=142.5
e. The output from a signal conditioning amplifier for a temperature of 245oC
=142.5*20
Gain= V out
V ∈¿ ¿
=20= V out
142.5mV
Vout=142.5*20
=2,850mV
=2.85V
f. The digital word output from A to D converter for a temperature
Accuracy of better than 750 μV
285+750μV or 285-750μV
Task 7
a. The required amplifier gain to give a transfer function of 7.8V/rad/s
0.35V/rad/s=1
7.8V/rad/s= ?
=7.8* 1
0.35
=22.23
b. The new transfer function if gearbox ratio was changed to 9 to 1(N=9)
45 rad/s =2
? =9

=45* 9
2
=202.5 rad/s
c. The output velocity for an input voltage of 4.5V (with N=9)
When N=9, 202.5 rad/s
=4.5V/202.5rad/s
=0.022V/rad/s
d. The input voltage for an output velocity of 80 rad-s(with N=9)
=0.022V/rad/s=N=9
When velocity =80rad/s
=0.022*80
=1.76V
Task 8
a. Explain briefly why damping is necessary
Damping in positional control system is used to prevent any vibrations so as
to enable the object to return to its position instantaneously.
b. There are four recognized degrees of damping. Identify each condition and
briefly describe in your own words its effect on positional control system.
Overdamped. In this degree, oscillations do not have an effect on the system.
Only the large amount of restraint placed on the servo can lead to increased
challenges in the system.
Underdamped. In this degree there is a quick response to any notable error signal. However,
the low amount of restraining force on the servo leads to errors in synchronization
Critically damped. In this degree, the system returns to equilibrium
instantaneously without any further oscillations.
Undamped. In this degree, the system oscillates at its natural resonance frequency
(ωo).
PART 2
Task 1
I. Y=2X3 cos X
Let u=2X3 v=cos x
du/dx=uv’ + vu’
=2x3(-cos x) + cos x(6x)
=-2x3cosx + 6xcosx

=cosx(-2x3+ 6x)
II. x 2−1
sin x
=let u=x2-1 and v=sin x
vu'−v ’u
v 2
= sinx (2 x ) – (x 2−1)(cos x)
sin2 X
= 2 xsinx−x 2cosx −cosx
sin2 X
III. Y=(2x3 -5x)5
= dy
dx = dy
du / * du
dx
=let u=2x3-5x and y=u5
du
dx =6x2-5 and dy
du =5u4
=(5u4)(6x2-5)
=5(2x3 -5x)4 (6x2-5)
Task 2
I. Sinh-1(2x)
Find the 1st derivative
dy
dx sinh^-1(2x)¿ 2(−1+ e2
2 e )^-1
d2 y
dx2 = dy
dx ¿2(−1+ e2
2 e )^-1)

¿ dy
dx ¿2(−1+ e2
2 e )^-1)=0
Thus Sinh^-1(2x) ¿ 0
II. r = (1 +¿ )2)3/12/ d 2 y
dx 2
y= 2
x
dy
dx =2lnx
d 2 y
dx 2 ¿ 2
X ¿
r = ( (1 + ( 2
X )2)/2/lnx)3/2
r =[ x ¿ ¿ ]3/2
III. y = ln3√x + 1
= d2 y
dx2 (ln3√x + 1)
= dy
dx (ln3√x + 1) = ln 3
2 √ x
=ln(3) 1
2X1/2-1
= ln 3
2 √ x
= d2 y
dx2
= dy
dx ¿ ln 3
2 √ x )
= −ln 3
4 X¿/2 ¿

Task 3
a.
∫x √ (2x2 +1)dx
Let u=2x2+1 ⟶ dx=1/4x du
= 1
4 ∫√udu
∫√udu
Applying power rule:
=2u 3/2 /
= 1
4 ∫√udu
== u3 /2
6
substitution back u= 2x2+1
== (2 x 2+1)3 /2
6
Hence
∫x√2x2+1dx
= (2 x 2+1)3 /2
6 +C
b.
∫ 4 x−16
( x−3)(x +1) dx
=4∫ x−4
¿ ¿ dx
∫x−4(x−3)(x+1)dx
Perform partial fraction decomposition:

=∫ 5
4 (x+1)− 1
4 (x−3))dx
= 5
4 ∫1x+1dx− 1
4 ∫1x−3dx
∫1x+1dx
Substitute u=x+1 ⟶ dx=du
=∫1udu
=ln(u)
substitution back u= x+1:
=ln (x+1)
∫1x−3dx
Substitute u=x−3 ⟶ dx=du
=∫1udu
=ln(u)
substitution back u=x−3:
=ln(x−3)
54∫1x+1dx−14∫1x−3dx
=5ln(x+1)4−ln(x−3)4
4∫x−4(x−3)(x+1)dx
=5ln(x+1)−ln(x−3)
Hence
∫4x−16/(x−3)(x+1)dx
=5ln(|x+1|)−ln(|x−3|)+C
c. ∫(x2−2x)eXdx
Integrate by parts: ∫fg′=fg−∫f′g
f =x2−2x, g’=ex
f′ =2x−2, g =ex
=(x2−2x)ex−∫(2x−2)exdx
Now solving:
∫(2x−2)exdx
Apply linearity:
=2∫(x−1)exdx

Now solving:
∫(x−1)exdx
Integrate by parts: ∫fg′=fg−∫f′g
=(x−1)ex−∫exdx
∫exdx
=ex
(x−1)ex−∫exdx
=(x−1)ex−ex
2∫(x−1)exdx
=2(x−1)ex−2ex
(x2−2x)ex−∫(2x−2)ex dx
= (x2−2x)ex −2(x−1)ex+2ex
=(x2 – 4x -4)ex
Task 4
a. A=80x-( 2+ ℼ
2 )x2
At maximum area
= dA
dX =80 – 2(2+ ℼ
2 )x=0
=2( 2+ ℼ
2 )x=80
=x=
80
2(2+ ℼ
2 )
X==
40
(2+ ℼ
2 )
X= 11.2m

b. Y== 3
√ (1+ 4 x )
∫y=3∫(1+4x)-1/2 dx
== 3 ¿ ¿
=6(1+4x)1/2 +c
Bibliography
Bagad, V.S. (2009). Mechatronics (4th revised ed.). Pune: Technical Publications. ISBN
9788184314908. Retrieved 28 June 2014.
Crew, Henry (2008). The Principles of Mechanics. BiblioBazaar, LLC. p. 43. ISBN 978-0-559-
36871-4.
Edmund Landau. ISBN 0-8218-2830-4 Differential and Integral Calculus, American
Mathematical Society.
Thomas, George B., Maurice D. Weir, Joel Hass, Frank R. Giordano (2008), Calculus, 11th ed.,
Addison-Wesley. ISBN 0-321-48987-X.