Solving Problems with Sinusoidal Waves and Vector Functions - EE

This assignment provides a comprehensive solution to problems involving sinusoidal waves and vector functions, crucial concepts in electrical engineering. The solution covers definitions of amplitude, periodic time, frequency, and phase shift, along with calculations for current in a circuit. It includes diagrams and calculations for force, moment, compound angle identities, and differentiation and integration problems. The assignment also explores the rate of change of voltage and particle speed, and it delves into the concept of charge and discharge in a circuit. Finally, the assignment determines maxima and minima of functions using calculus, offering a complete and practical guide to these fundamental engineering principles.

Use analytical and computational
methods for solving problems by
relating sinusoidal wave

Task 1
(a) Define –
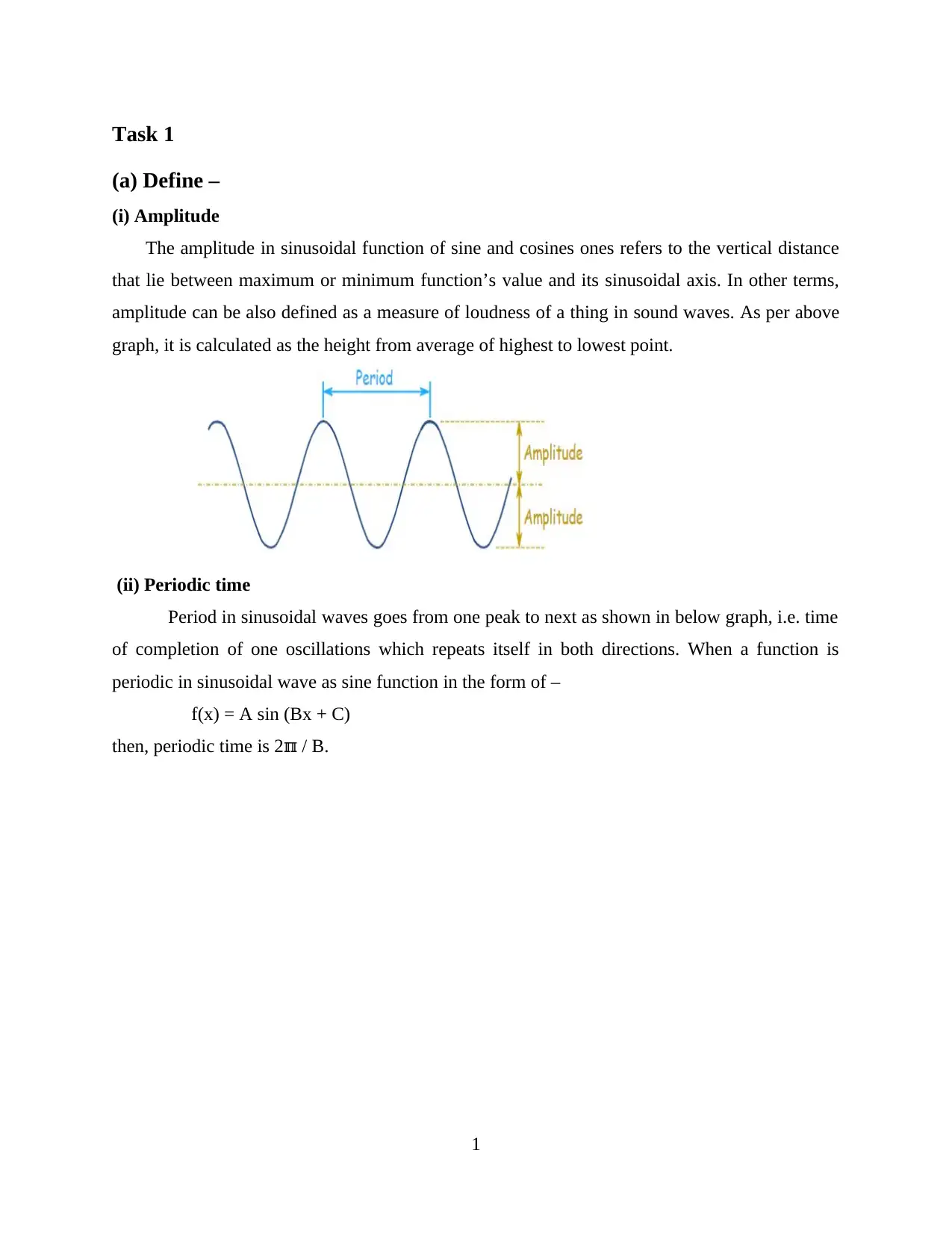
(i) Amplitude
The amplitude in sinusoidal function of sine and cosines ones refers to the vertical distance
that lie between maximum or minimum function’s value and its sinusoidal axis. In other terms,
amplitude can be also defined as a measure of loudness of a thing in sound waves. As per above
graph, it is calculated as the height from average of highest to lowest point.
(ii) Periodic time
Period in sinusoidal waves goes from one peak to next as shown in below graph, i.e. time
of completion of one oscillations which repeats itself in both directions. When a function is
periodic in sinusoidal wave as sine function in the form of –
f(x) = A sin (Bx + C)
then, periodic time is 2 / B.ℼ
1

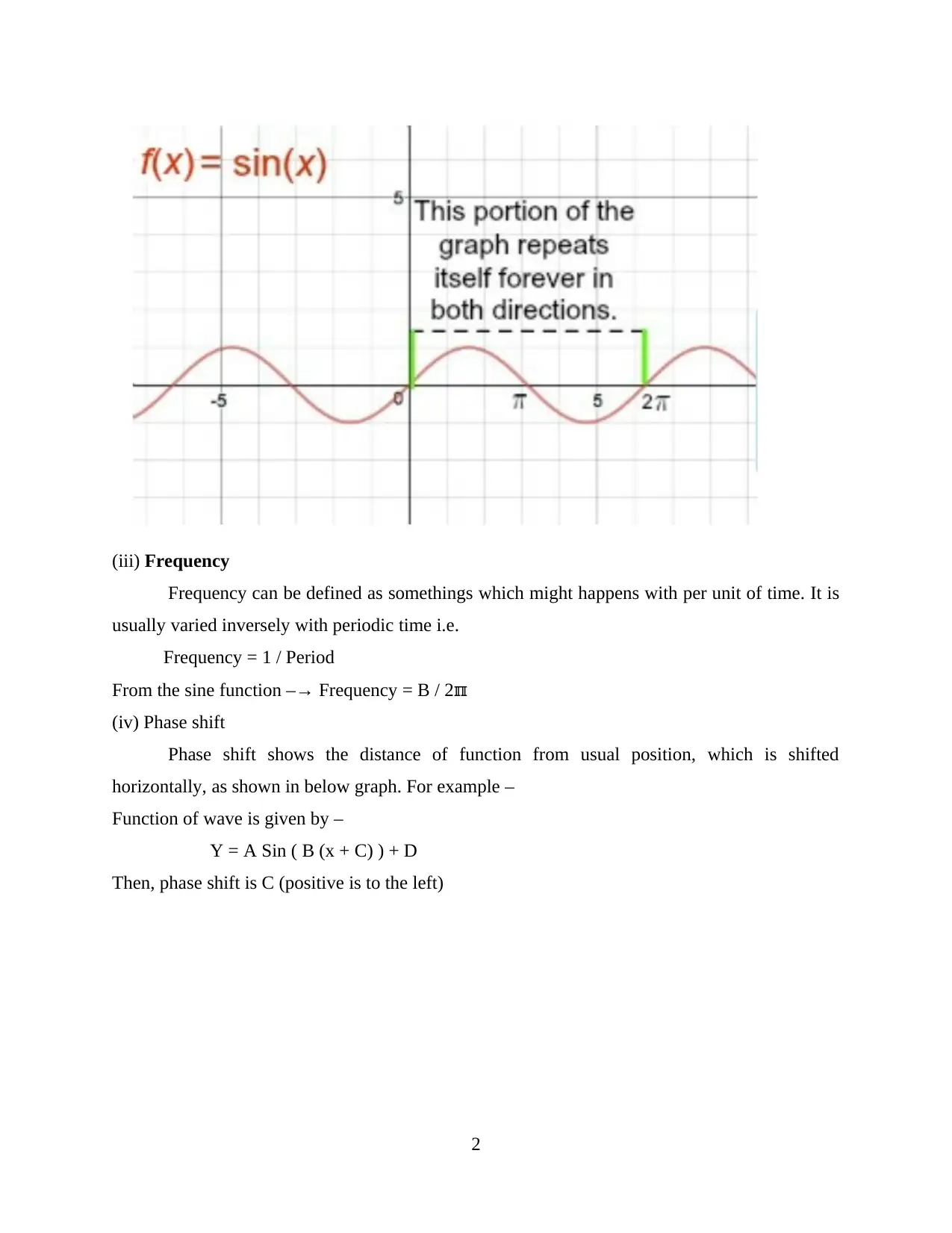
(iii) Frequency
Frequency can be defined as somethings which might happens with per unit of time. It is
usually varied inversely with periodic time i.e.
Frequency = 1 / Period
From the sine function –→ Frequency = B / 2ℼ
(iv) Phase shift
Phase shift shows the distance of function from usual position, which is shifted
horizontally, as shown in below graph. For example –
Function of wave is given by –
Y = A Sin ( B (x + C) ) + D
Then, phase shift is C (positive is to the left)
2

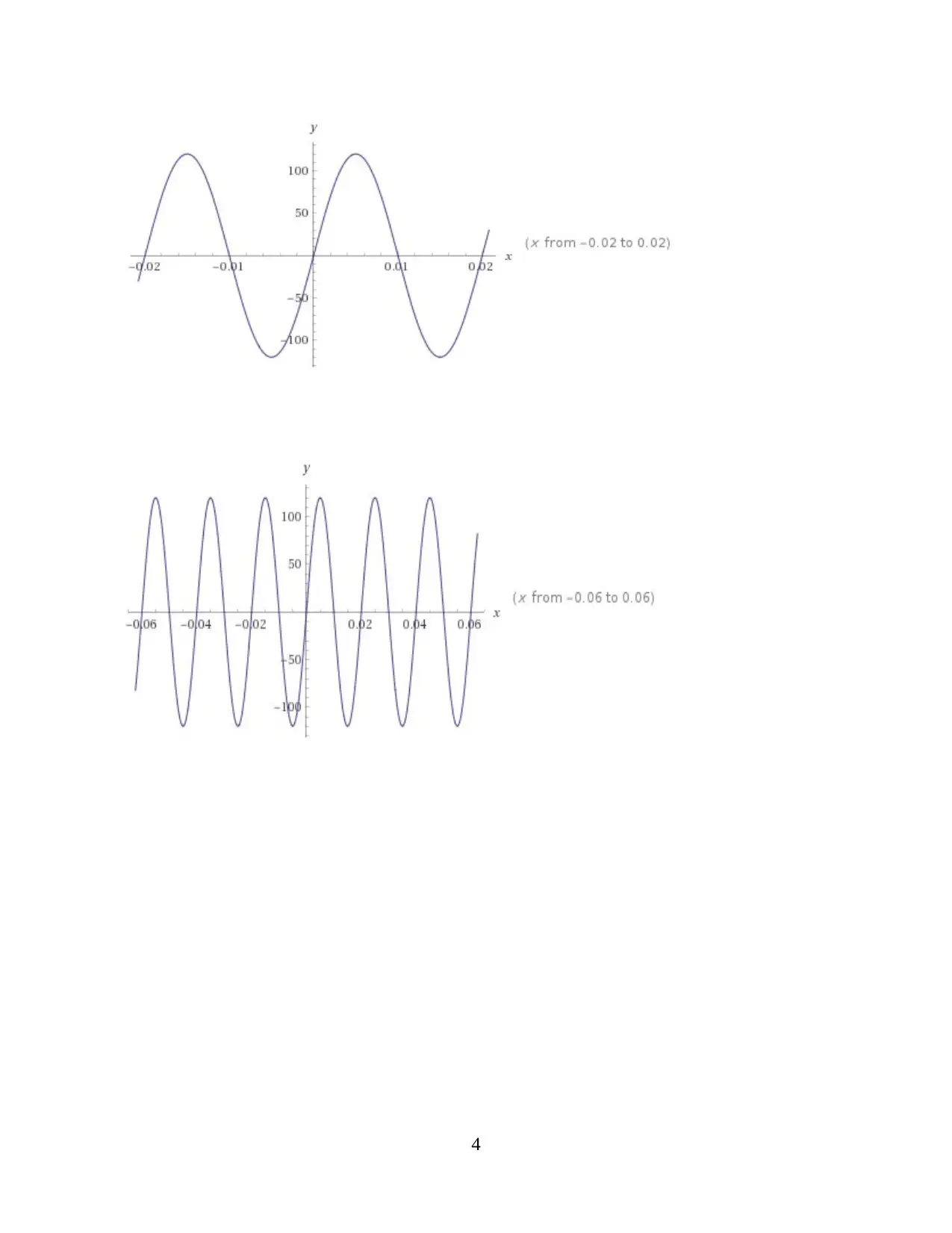
b) The current in a circuit at any time t is given by
I = 120 sin (100ℼt) Amps
(i) To determine Amplitude, periodic time and frequency
Solution: The generalised form of equation is
Y = A Sin ( B (x + C) ) + D
Therefore, comparing it with given equation
I = 120 sin (100ℼt) Amps
Amplitude is A = 120
Periodic time is 2 / B = 2 / 100 = 0.02ℼ ℼ ℼ
Phase shift is C = 0
Frequency = 1 / Period time = 1/0.02 = 50
(ii) Diagram of curve of the current for I cycle
3

4

TASK 2
(a) Given electric current I = 3i – 4j + k
Magnetic field B = 0i + 1j – 8k
Then, force per unit length acting on the conductor can be determined by –
F = n I. L. B. sin Ө
Using Right Hand Rule, Ө = 90ᵒ
Therefore, at Ө = 90, n = 1
F = I.B sin Ө
= (3i – 4j + k) (0i + 1j – 8k) sin 90
= (3.0)i.i + (-4.1)j.j + (1. -8)k.k
= 0 – 4 – 8 = -12 Newton
(b) given force F = 3i – 4j + k
Passes through point P = 4i – 1j + 5k
Q = 4i + 0.j – 3.k
→ → →
Then PQ = Q – P
= (4i + 0.j – 3.k) – (4i – 1j + 5k)
= 0.i – 1.j – 8 k
Therefore, Moment of the force M can be determined by
→ →
M = PQ x F
i j k
= 0 -1 -8
3 -4 1
= (1 x -1 – (-8 x -4)) i – (0 x 1 – 3 x -8) j + (0 x -4 – 3 x -1) k
= -33i – 24j + 3k
While, magnitude of moment M = √332 + 242 + 32
= √1674 = 40.91
5

TASK 3
(a) sin sin(P) = 0.8892 and cos cos(Q) = 0.6946
To determine, cos cos(P) and sin sin(Q), use compound formula in following way –
sin sin(P) + cos cos(P) = 1
then, 0.8892 + cos cos(P) = 1
or, cos cos(P) = 1 – 0.8892
= 0.1108
Similarly,
sin sin(Q) + cos cos(Q) = 1
then, sin sin(Q) + 0.6946 = 1
or, cos cos(P) = 1 – 0.6946
= 0.3054
6

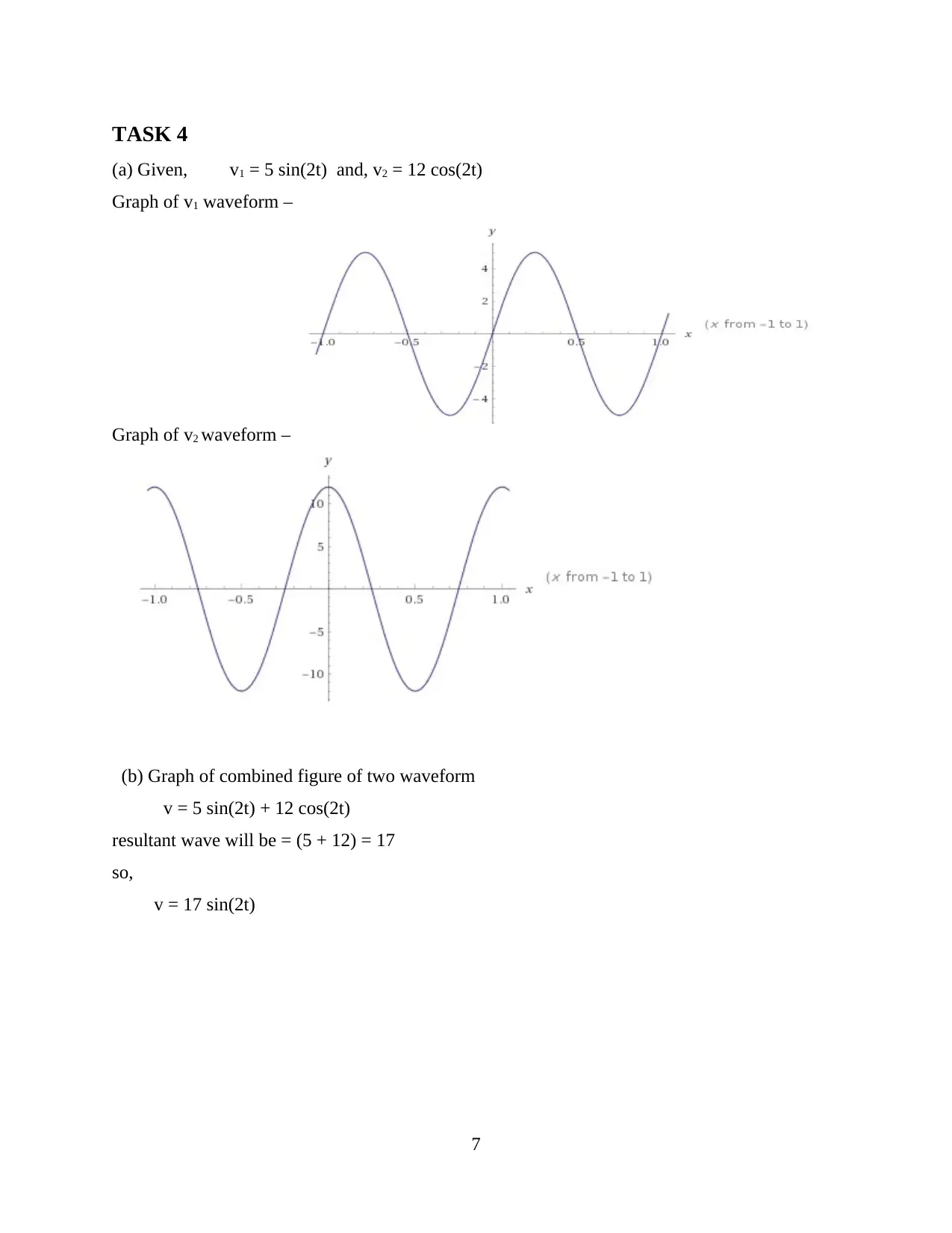
TASK 4
(a) Given, v1 = 5 sin(2t) and, v2 = 12 cos(2t)
Graph of v1 waveform –
Graph of v2 waveform –
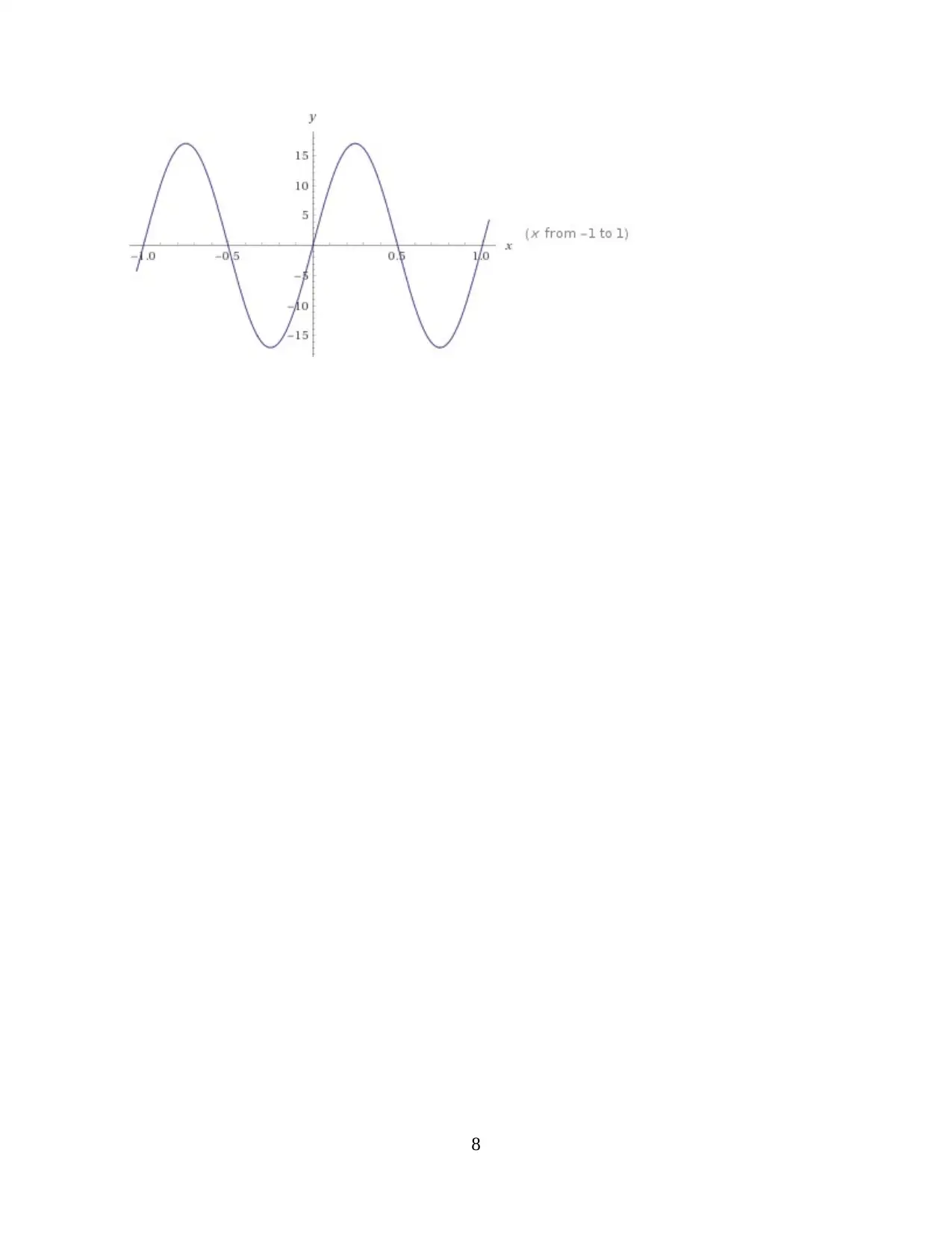
(b) Graph of combined figure of two waveform
v = 5 sin(2t) + 12 cos(2t)
resultant wave will be = (5 + 12) = 17
so,
v = 17 sin(2t)
7

8

TASK 5
(a) V = 3t2 – 4t + 6/t + e2t Volts
Rate of change of voltage with time can be calculated by differentiating above equation with
respect to t as
dV = d (3t2 – 4t + 6/t + e2t)
dt dt
= 6t – 4 + 6/t2 + 2 e2t
At, t = 0.05 sec
= 6 (0.05) – 4 + 6/ (0.05)2 + 2 e2 (0.05)
= 2398.4 volts.
(b) V = ln ln (t) + 6t2 Volts
dV = d (ln ln (t) + 6t2)
dt dt
= (1/ t log t) + 12 t
At, t = 0.05 sec
= (1 / 0.05 log 0.05) + 12 x 0.05
= -14.78 volts.
(c) V = 0.015 sin sin (0.01 t) Voltsℼ
dV = d (0.015 sin sin (0.01 t))ℼ
dt dt
= 0.015 cos sin (0.01 t) cos (0.01 t) 0.01ℼ ℼ ℼ
= 0.00015 cos sin (0.01 t) cos (0.01 t)ℼ ℼ ℼ
At, t = 0.05 sec
= 0.00015 cos sin (0.01 x 0.05) cos (0.01 x 0.05)ℼ ℼ ℼ
= 0.00015 cos sin (0.0005 ) cos (0.0005 )ℼ ℼ ℼ
= 0.0005 volts.
9

(d) s = 3t2 – 4t + 6/t + e2t metres
Particle’s speed with time can be calculated by differentiating above equation with respect to t as
ds = d (3t2 – 4t + 6/t + e2t)
dt dt
= 6t – 4 + 6/t2 + 2 e2t
At, t = 0.05 sec
= 6 (0.05) – 4 + 6/ (0.05)2 + 2 e2 (0.05)
= 2398.4 metres
(e) s = ln ln (t) + 6t2 metres
ds = d (ln ln (t) + 6t2)
dt dt
= (1/ t log t) + 12 t
At, t = 0.05 sec
= (1 / 0.05 log 0.05) + 12 x 0.05
= -14.78 metres.
(f) s = 0.015 sin sin (0.01 t) metresℼ
ds = d (0.015 sin sin (0.01 t))ℼ
dt dt
= 0.015 cos sin (0.01 t) cos (0.01 t) 0.01ℼ ℼ ℼ
= 0.00015 cos sin (0.01 t) cos (0.01 t)ℼ ℼ ℼ
At, t = 0.05 sec
= 0.00015 cos sin (0.01 x 0.05) cos (0.01 x 0.05)ℼ ℼ ℼ
= 0.00015 cos sin (0.0005 ) cos (0.0005 )ℼ ℼ ℼ
= 0.0005 metres
10

TASK 6
(a) Given, I = 3t2 + 4 ms-2
Expression for charge can be calculated by integrating the current with respect to time in
following way –
∫ I. dt = ∫ (3t2 + 4) . dt
= t3 + 4t Coulombs
(b) Given, v = 3t2 + 4 ms-2
Speed can be calculated by integrating the velocity with respect to time as –
∫ v. dt = ∫ (3t2 + 4) . dt
= t3 + 4t metres
(c) Variable force F is given by
F = 2 e-4s N
Work done by this force can be calculated by
b
W =∫ F.ds
a
b
W =∫ 2 e-4s.ds
a
b
= [2/4. e-4s ] a
= ½ e-4 (b - a)
Work done by force at 3.50m to 4.75m
= ½ e-4 (4.75 – 3.50)
= ½ e-6
= 0.0012 Joule
11

TASK 7
(a) Charges Q (coulombs) at a time t seconds is given as
R dQ + Q = 0
dt C
Here, C is the capacitance and R is the resistance
Differentiating the given equation when t = 0,
Using integration calculus and apply Kirchoff’s loop rule –
IR – Q/C = 0
Where I = dQ/dt
Then,
R (dQ/dt) = -Q/C
Solving this differential equation –
Q(t) = Q0 .e-t/τ
Here, Q0 denotes the initial charge at constant time τ = RC on the capacitor
Therefore,
I(t) = - (Q0/RC) e-t/τ
At t = 0, I = I0
Then,
I(t) = -I0 e-t/τ
(b) Resistance = 250 x 103 ohm and a capacitance = 8.5 x 10-6 Farads
To determine –
(i) initial charge
Initial charge at 0.32T = 0.32RC
= 0.32 (250 x 103) (8.0)
= 6.4 x 106
(ii) charge after one second
1T = 1RC
= (250 x 103) (8.5 x 10-6)
= 2.125
12

TASK 8
(a) Given,
V = 24t – 3t2
Maxima and minima can be determined by using calculus derivative in following way –
dV = d (24t – 3t2)
dt dt
= 24 – 6t
Again differentiating with respect to t
d2V = d (24 – 6t)
dt2 dt
= – 6 < 0
This implies that function attains its maximum value.
Therefore, maximum value of given function is –
dV/dt = 0
24 – 6t = 0
Or, t = 4
Therefore, maximum voltage will reach at t = 4 sec
Put this value in given equation of voltage –
V = 24 x 4 – 3 x 42
= 96 – 48 = 48volts
This implies that at t = 4sec, function has attained maximum value.
(b) Resistance in a circuit is given by –
R = 10V3 + 30V2 + V
Applying the calculus derivate, to determine maxima or minima as –
dR = d (10V3 + 30V2 + V)
dt dt
= 30V2 + 60V + 1
13

Again differentiate it with respect to t –
d2R = d (30 V2 + 60 V + 1)
dt2 dt
= 60V + 60 V
Again differentiate it with respect to t –
d3R = d (60V + 60)
dt3 dt
= 60 > 0
Therefore, the given resistance attains minimum value at dR/dt = 0
30V2 + 60V + 1 = 0
Or, V = 2 or 0 approx.
Therefore, resistance attains minimum value at V = 0
i.e. R = 1ohm
14