AMME 2700 Instrumentation Assignment Solution - Circuits Analysis
VerifiedAdded on 2023/01/16
|26
|1239
|93
Homework Assignment
AI Summary
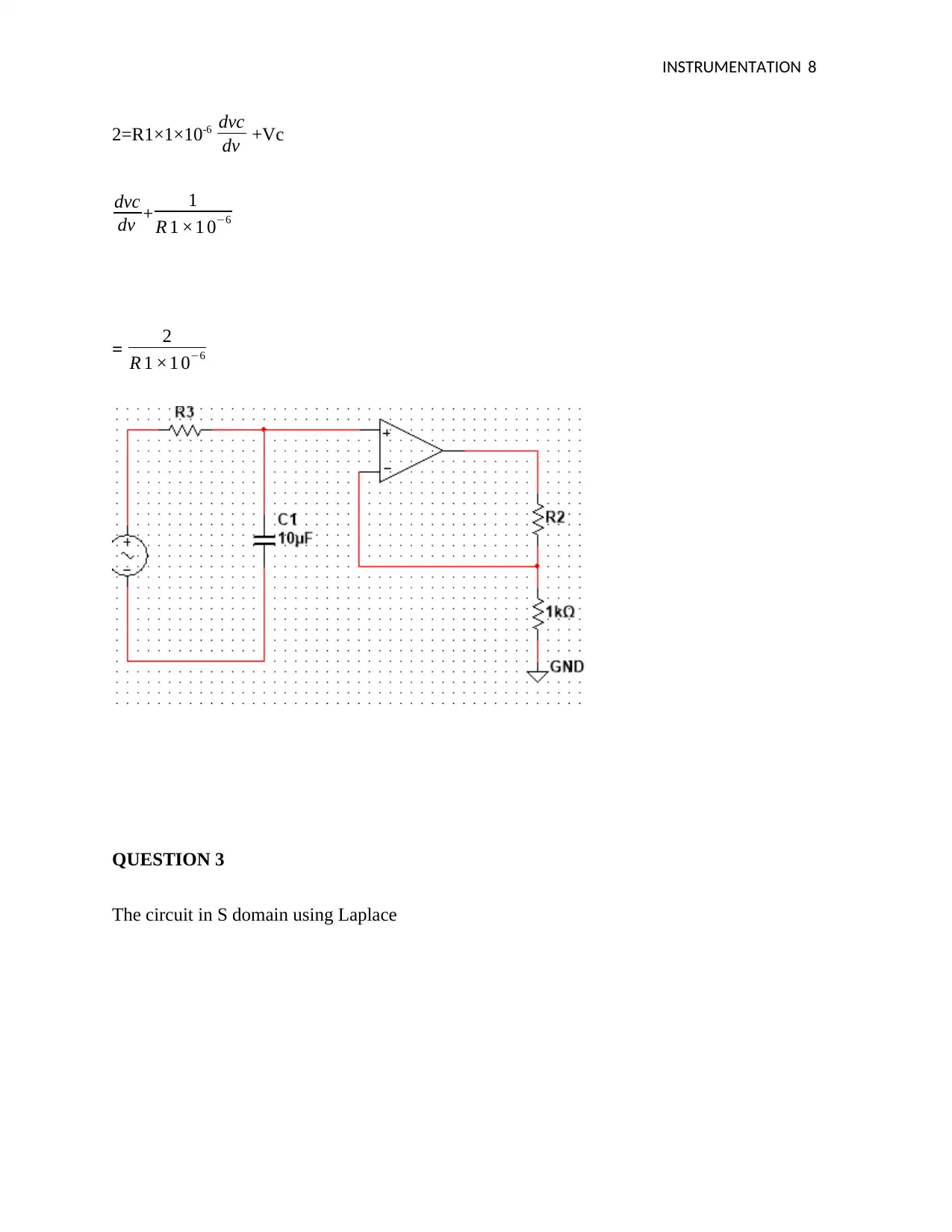
This document presents a comprehensive solution to an instrumentation assignment, addressing several key concepts in electrical circuit analysis. The solution begins with the application of Laplace transforms and nodal analysis to determine circuit behavior, followed by calculations involving inductor currents and voltage drops. The assignment then delves into circuit analysis in the S-domain, including characteristic equations, standard forms, and the application of inverse Laplace transforms. Further, the solution explores operational amplifier (op-amp) circuits, calculating component values and analyzing circuit behavior. It covers the analysis of op-amp circuits, including gain calculations and component determination, and culminates with Bode plots and the design of a Salley Key bandpass filter, providing a complete and detailed solution to the assignment questions.
1 out of 26

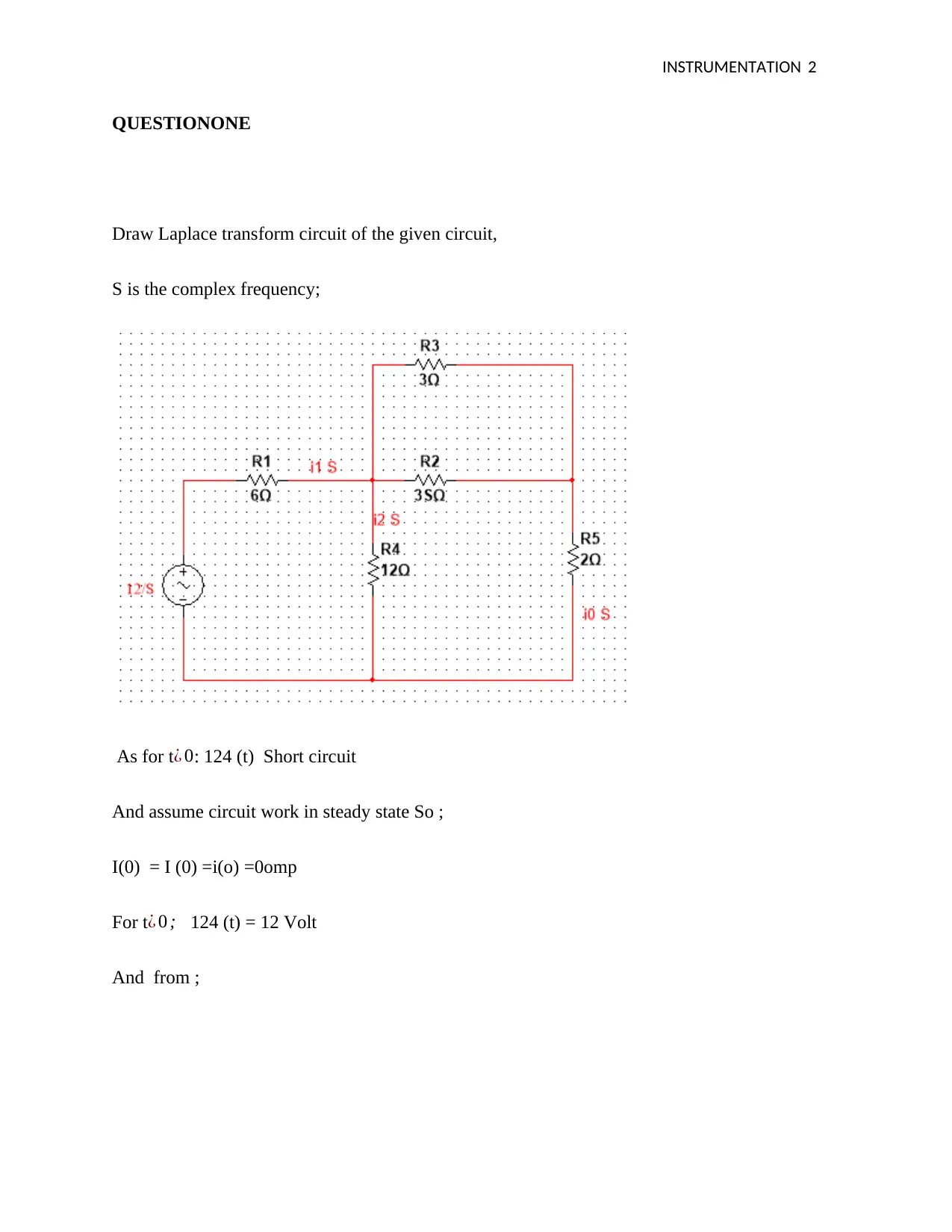
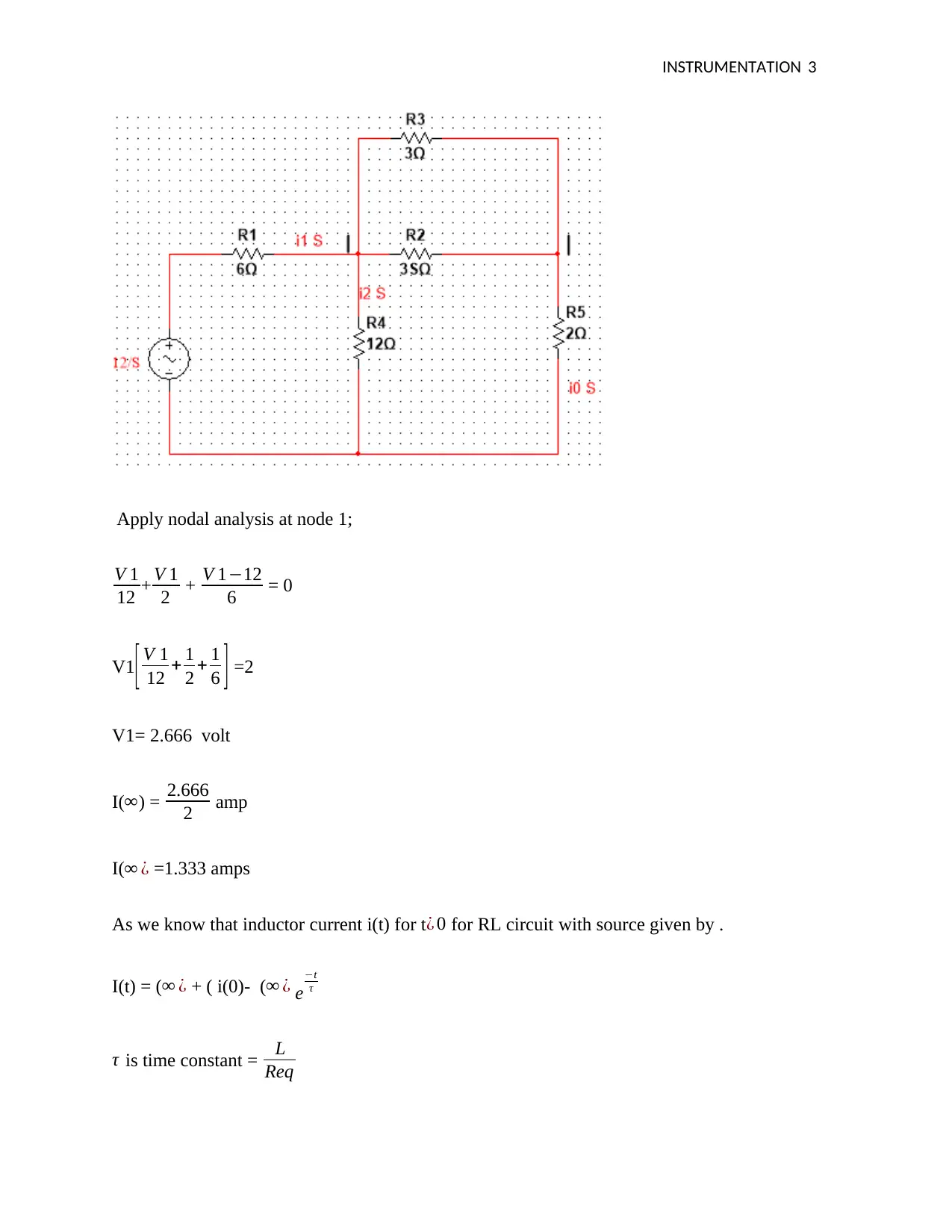


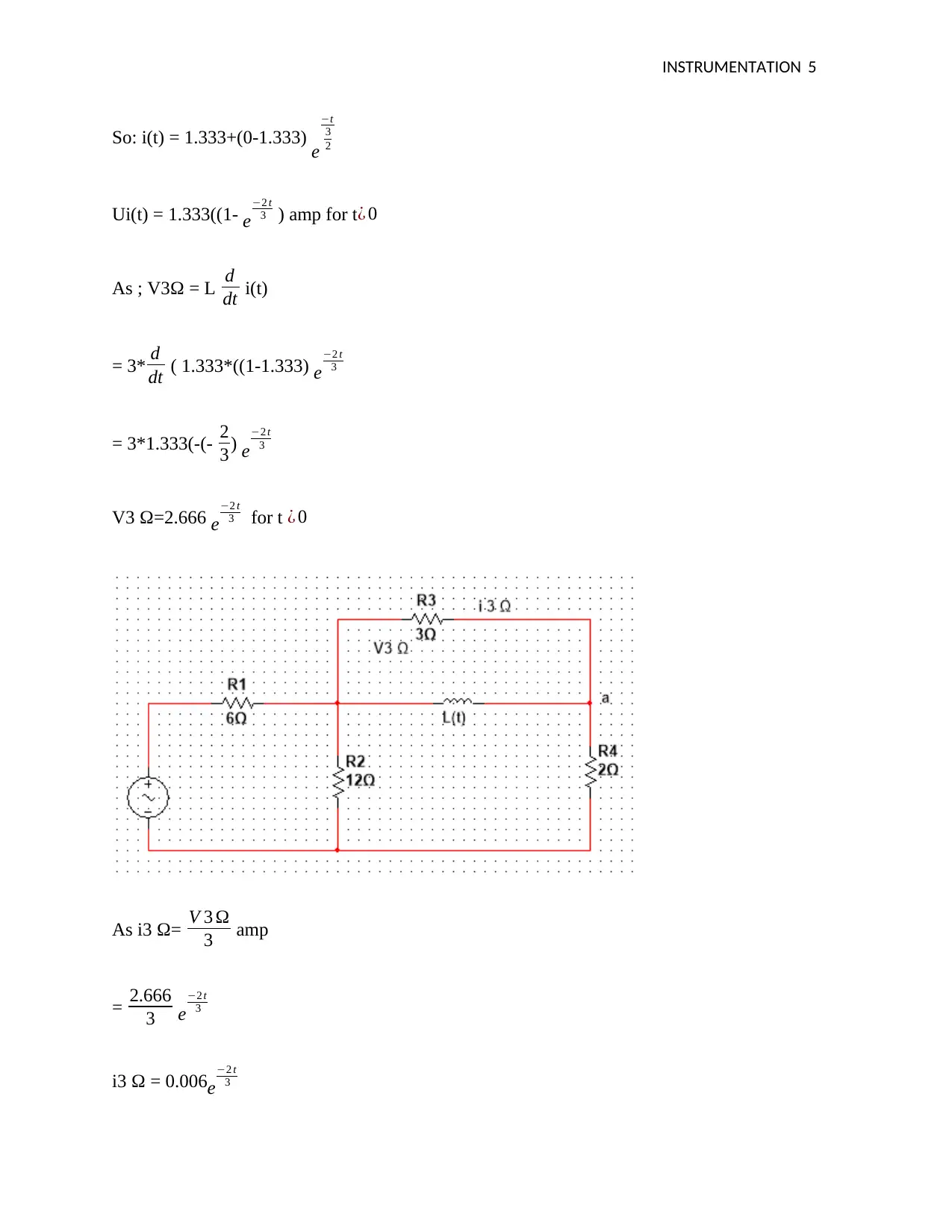

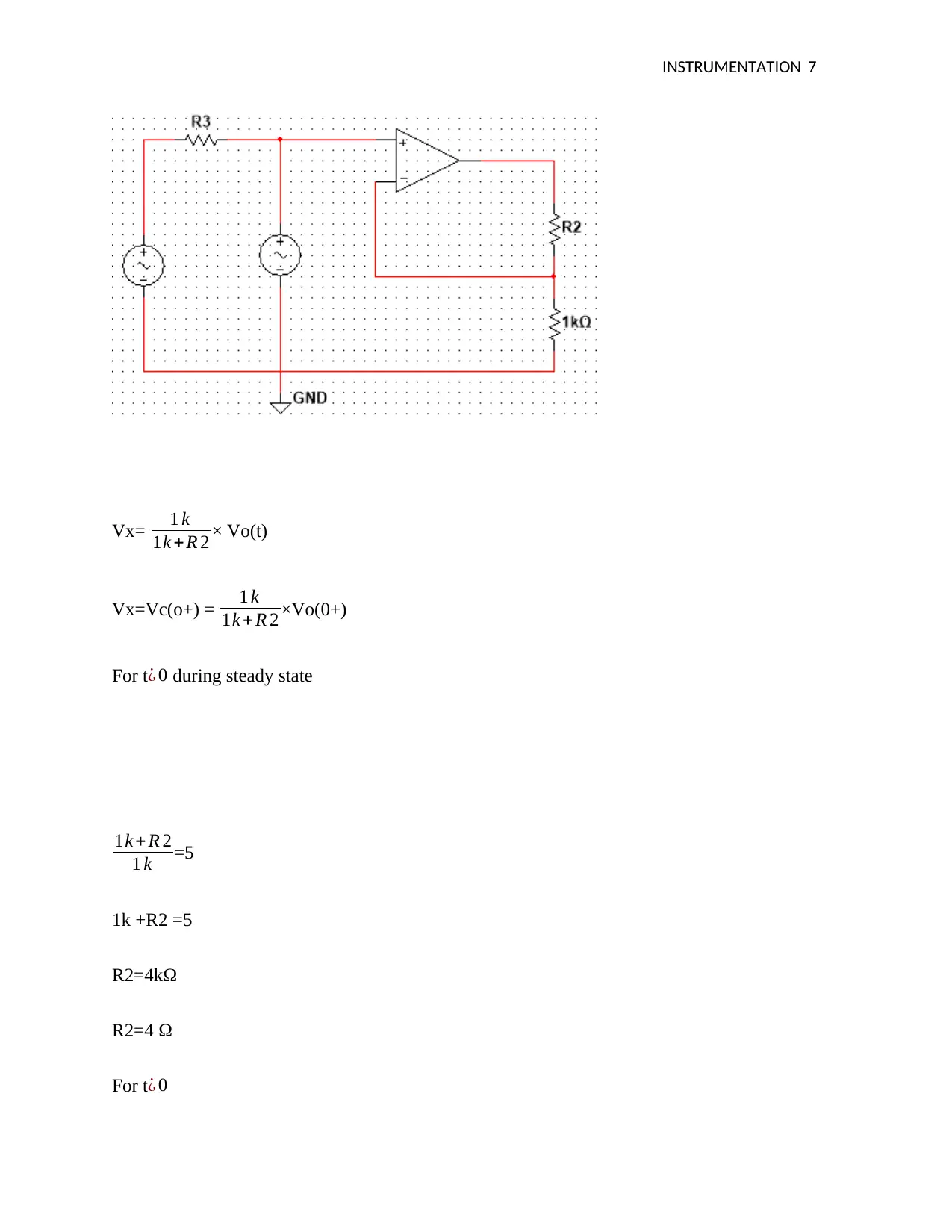









![[object Object]](/_next/static/media/star-bottom.7253800d.svg)