Electrical Engineering: Transient Analysis and Stability Homework
VerifiedAdded on 2022/09/27
|13
|1513
|19
Homework Assignment
AI Summary
This document presents a comprehensive solution to an electrical engineering assignment focusing on transient analysis, stability, and surge protection. The solution begins with an analysis of synchronous generators, including equations for rotor angle and generator frequency, and calculations for critical clearing time and angle. It then provides MATLAB code for simulating system behavior, including frequency and rotor angle variations. The assignment further explores impediments to adopting renewable energy resources in existing grids, along with potential solutions. MATLAB code is used to analyze the impact of system parameters, such as inertia constant (H) and damping coefficient (D), on frequency response. The document also provides a detailed discussion on the impact of H and D on frequency and offers conclusions. Figures and graphs are included to illustrate the results, and references are provided for further reading.
1 out of 13








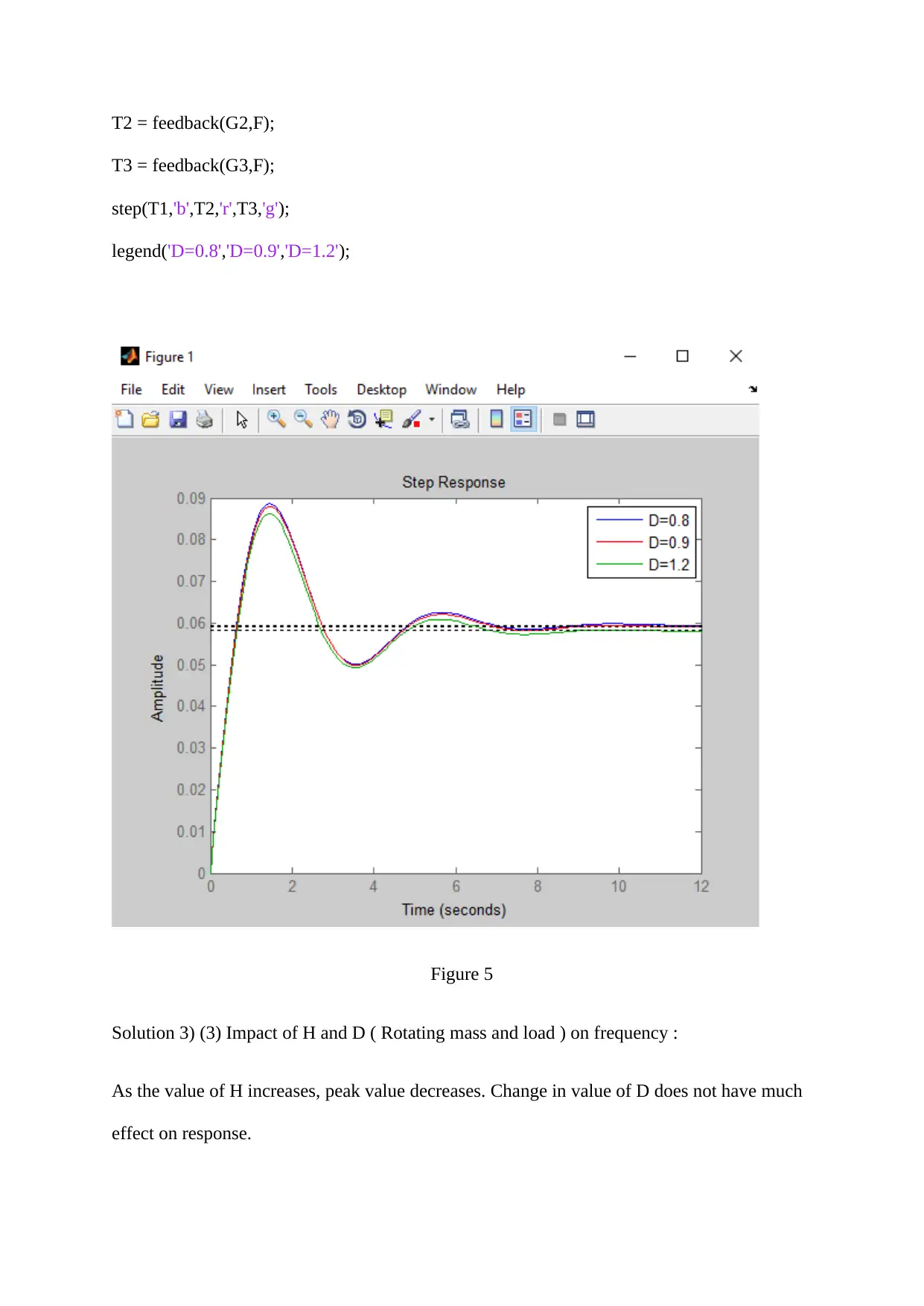
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)