Engineering Maths Assignment: Statistics, Calculus, and Vectors
VerifiedAdded on 2023/01/12
|16
|1703
|66
Homework Assignment
AI Summary
This engineering maths assignment covers a range of topics, including calculating the mean and standard deviation from a set of observations, and applying the normal distribution to approximate binomial distributions. It explores the relationship between motor lifetime and normal distribution, calculating probabilities of rejection and analyzing profitability. The assignment also delves into trigonometric functions, vector operations, and calculus problems, such as finding the power produced by a solar system and solving for stationary points, maxima, and minima using derivatives. Solutions include detailed calculations and explanations for each problem, providing a comprehensive understanding of the concepts and their applications in engineering contexts. The assignment aims to enhance students' problem-solving skills in mathematics and its relevance to engineering.

ENGINEERING MATHS
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

TABLE OF CONTENTS
LO2..................................................................................................................................................3
A. Mean and standard deviation..................................................................................................3
B. Normal distribution approximation for binomial distribution................................................3
C...................................................................................................................................................4
D..................................................................................................................................................4
E.).................................................................................................................................................6
LO 3.................................................................................................................................................7
A..................................................................................................................................................7
D................................................................................................................................................10
E.................................................................................................................................................10
G................................................................................................................................................11
LO 4...............................................................................................................................................13
A................................................................................................................................................13
B.)..............................................................................................................................................13
C.)..............................................................................................................................................13
E.)...............................................................................................................................................15
LO2..................................................................................................................................................3
A. Mean and standard deviation..................................................................................................3
B. Normal distribution approximation for binomial distribution................................................3
C...................................................................................................................................................4
D..................................................................................................................................................4
E.).................................................................................................................................................6
LO 3.................................................................................................................................................7
A..................................................................................................................................................7
D................................................................................................................................................10
E.................................................................................................................................................10
G................................................................................................................................................11
LO 4...............................................................................................................................................13
A................................................................................................................................................13
B.)..............................................................................................................................................13
C.)..............................................................................................................................................13
E.)...............................................................................................................................................15
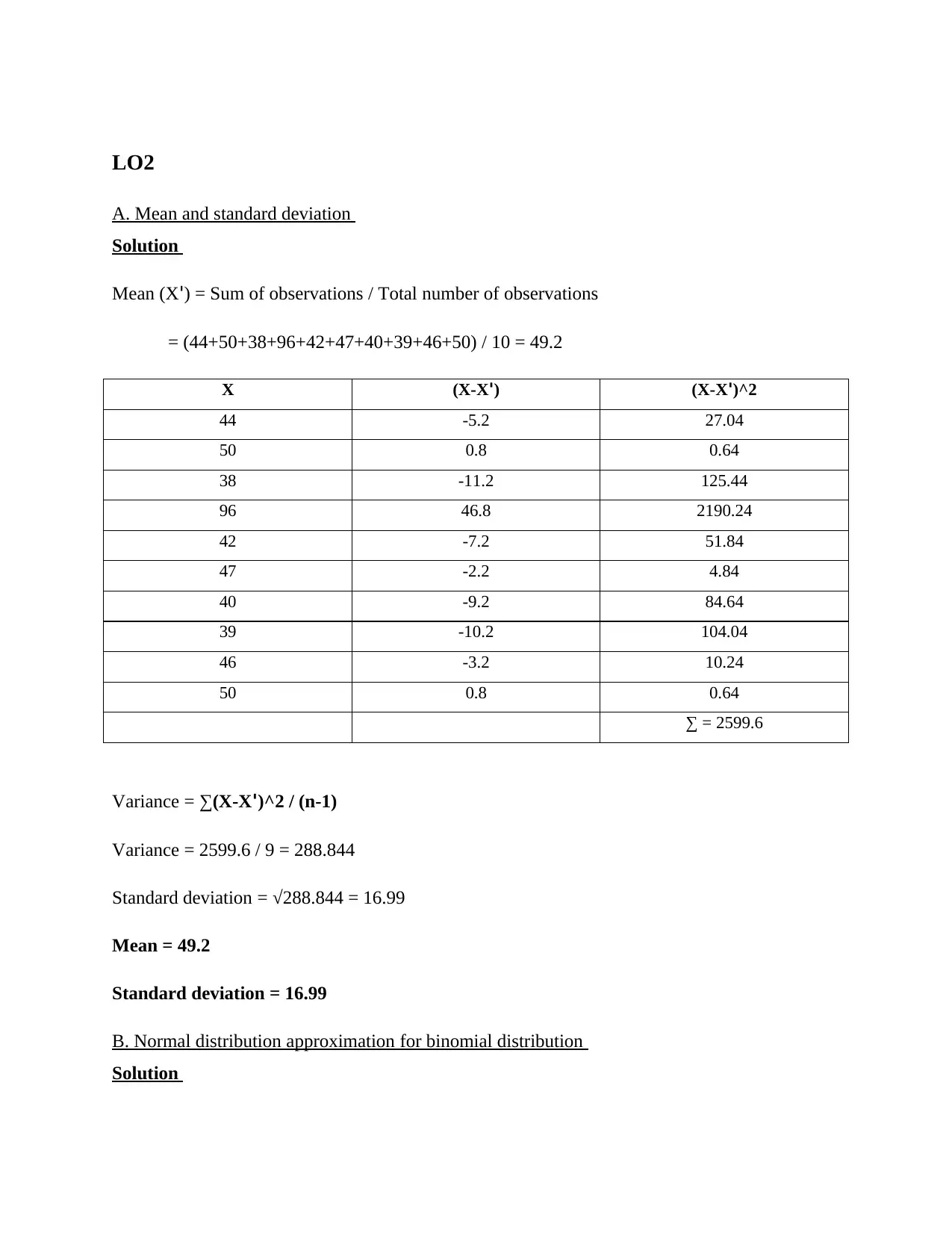
LO2
A. Mean and standard deviation
Solution
Mean (X') = Sum of observations / Total number of observations
= (44+50+38+96+42+47+40+39+46+50) / 10 = 49.2
X (X-X') (X-X')^2
44 -5.2 27.04
50 0.8 0.64
38 -11.2 125.44
96 46.8 2190.24
42 -7.2 51.84
47 -2.2 4.84
40 -9.2 84.64
39 -10.2 104.04
46 -3.2 10.24
50 0.8 0.64
∑ = 2599.6
Variance = ∑(X-X')^2 / (n-1)
Variance = 2599.6 / 9 = 288.844
Standard deviation = √288.844 = 16.99
Mean = 49.2
Standard deviation = 16.99
B. Normal distribution approximation for binomial distribution
Solution
A. Mean and standard deviation
Solution
Mean (X') = Sum of observations / Total number of observations
= (44+50+38+96+42+47+40+39+46+50) / 10 = 49.2
X (X-X') (X-X')^2
44 -5.2 27.04
50 0.8 0.64
38 -11.2 125.44
96 46.8 2190.24
42 -7.2 51.84
47 -2.2 4.84
40 -9.2 84.64
39 -10.2 104.04
46 -3.2 10.24
50 0.8 0.64
∑ = 2599.6
Variance = ∑(X-X')^2 / (n-1)
Variance = 2599.6 / 9 = 288.844
Standard deviation = √288.844 = 16.99
Mean = 49.2
Standard deviation = 16.99
B. Normal distribution approximation for binomial distribution
Solution
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

N = 20
P = 0.25
Mean = np = 20 * (0.25) = 5
Variance = np*(1-p) = 5*(1-0.25) = 3.75
Standard deviation = √3.75 = 1.94
Thus normal approximation: mean = 5 and standard deviation = 1.94
B (20, 0.25) and N (5, 1.94)
C.
Average life of motor = X' = 10
Standard deviation =σ = 2
Solution
Let x denotes the life of motors
Z value = (x - X') / σ
If life time is distributed normally then
3% area = Z – value of -1.88
-1.88 = (x-10) / 2
On solving we have x =6.24 years
Thus motors should be guaranteed for 6.24 years for normal
distribution.
P = 0.25
Mean = np = 20 * (0.25) = 5
Variance = np*(1-p) = 5*(1-0.25) = 3.75
Standard deviation = √3.75 = 1.94
Thus normal approximation: mean = 5 and standard deviation = 1.94
B (20, 0.25) and N (5, 1.94)
C.
Average life of motor = X' = 10
Standard deviation =σ = 2
Solution
Let x denotes the life of motors
Z value = (x - X') / σ
If life time is distributed normally then
3% area = Z – value of -1.88
-1.88 = (x-10) / 2
On solving we have x =6.24 years
Thus motors should be guaranteed for 6.24 years for normal
distribution.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

D.
Probability of rejection or failure = q = 12% or 0.12
n = 10
p = 0.88
Solution
Let x denotes number of rejected pistons
1.) Probability of not more than 2 pistons are rejected = P (x<=2)
= P (x=0) + P (x=1) + P (x=2)
P (x) = nCx*(pn) * [q(n-x)]
P (0) = 0.2785
P (1) = 0.3797
P (2) = 0.2330
P (x<=2) = 0.891
2.) Probability of at least 2 pistons are rejected = P (x>=2)
P (x>=2) = 1 - P (x<=1)
= 1 – [ P (x=0) + P (x=1) ]
P (0) = 0.2785
P (1) = 0.3797
P (x>=2) = 0.341
Probability of rejection or failure = q = 12% or 0.12
n = 10
p = 0.88
Solution
Let x denotes number of rejected pistons
1.) Probability of not more than 2 pistons are rejected = P (x<=2)
= P (x=0) + P (x=1) + P (x=2)
P (x) = nCx*(pn) * [q(n-x)]
P (0) = 0.2785
P (1) = 0.3797
P (2) = 0.2330
P (x<=2) = 0.891
2.) Probability of at least 2 pistons are rejected = P (x>=2)
P (x>=2) = 1 - P (x<=1)
= 1 – [ P (x=0) + P (x=1) ]
P (0) = 0.2785
P (1) = 0.3797
P (x>=2) = 0.341
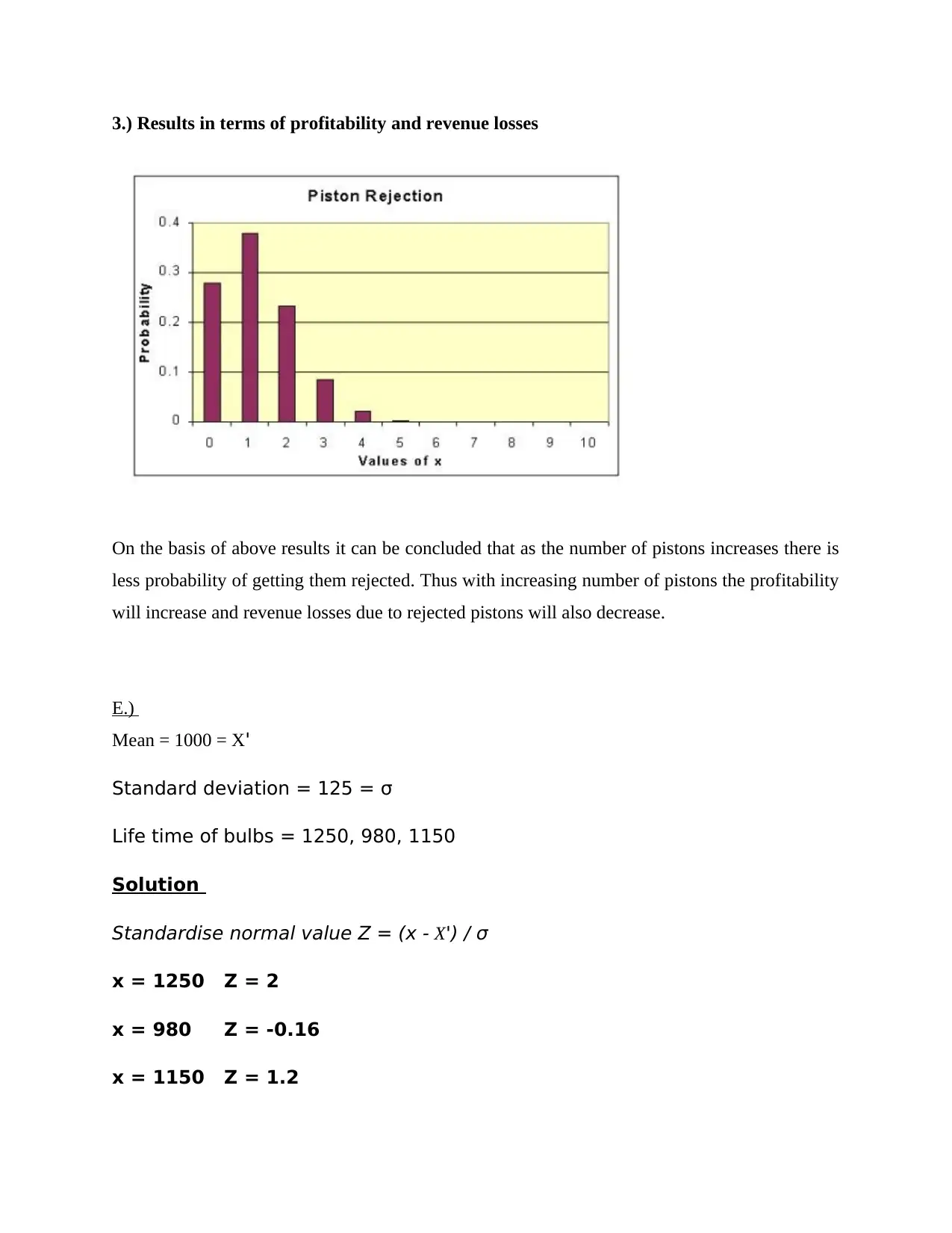
3.) Results in terms of profitability and revenue losses
On the basis of above results it can be concluded that as the number of pistons increases there is
less probability of getting them rejected. Thus with increasing number of pistons the profitability
will increase and revenue losses due to rejected pistons will also decrease.
E.)
Mean = 1000 = X'
Standard deviation = 125 = σ
Life time of bulbs = 1250, 980, 1150
Solution
Standardise normal value Z = (x - X') / σ
x = 1250 Z = 2
x = 980 Z = -0.16
x = 1150 Z = 1.2
On the basis of above results it can be concluded that as the number of pistons increases there is
less probability of getting them rejected. Thus with increasing number of pistons the profitability
will increase and revenue losses due to rejected pistons will also decrease.
E.)
Mean = 1000 = X'
Standard deviation = 125 = σ
Life time of bulbs = 1250, 980, 1150
Solution
Standardise normal value Z = (x - X') / σ
x = 1250 Z = 2
x = 980 Z = -0.16
x = 1150 Z = 1.2
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

LO 3
A.
P max = 20 kwh / day
P (t) = a cos [b (t-d)] +c
t = 0 denotes 1st January
Period of P (t) = 365 days [ February has 28 days]
P min = 4 kwh / day
Solution
1.)
C = (P max + P min) / 2
=( 20 +4 )/2 = 12
C = 12
Similarly |a| = (P max - P min) / 2
|a| = ( 20 -4 )/2 = 8
|a| = 8
Time over which p(t ) is maximum
Month Number of days
January 31
February 28
March 31
April 30
May 31
A.
P max = 20 kwh / day
P (t) = a cos [b (t-d)] +c
t = 0 denotes 1st January
Period of P (t) = 365 days [ February has 28 days]
P min = 4 kwh / day
Solution
1.)
C = (P max + P min) / 2
=( 20 +4 )/2 = 12
C = 12
Similarly |a| = (P max - P min) / 2
|a| = ( 20 -4 )/2 = 8
|a| = 8
Time over which p(t ) is maximum
Month Number of days
January 31
February 28
March 31
April 30
May 31
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
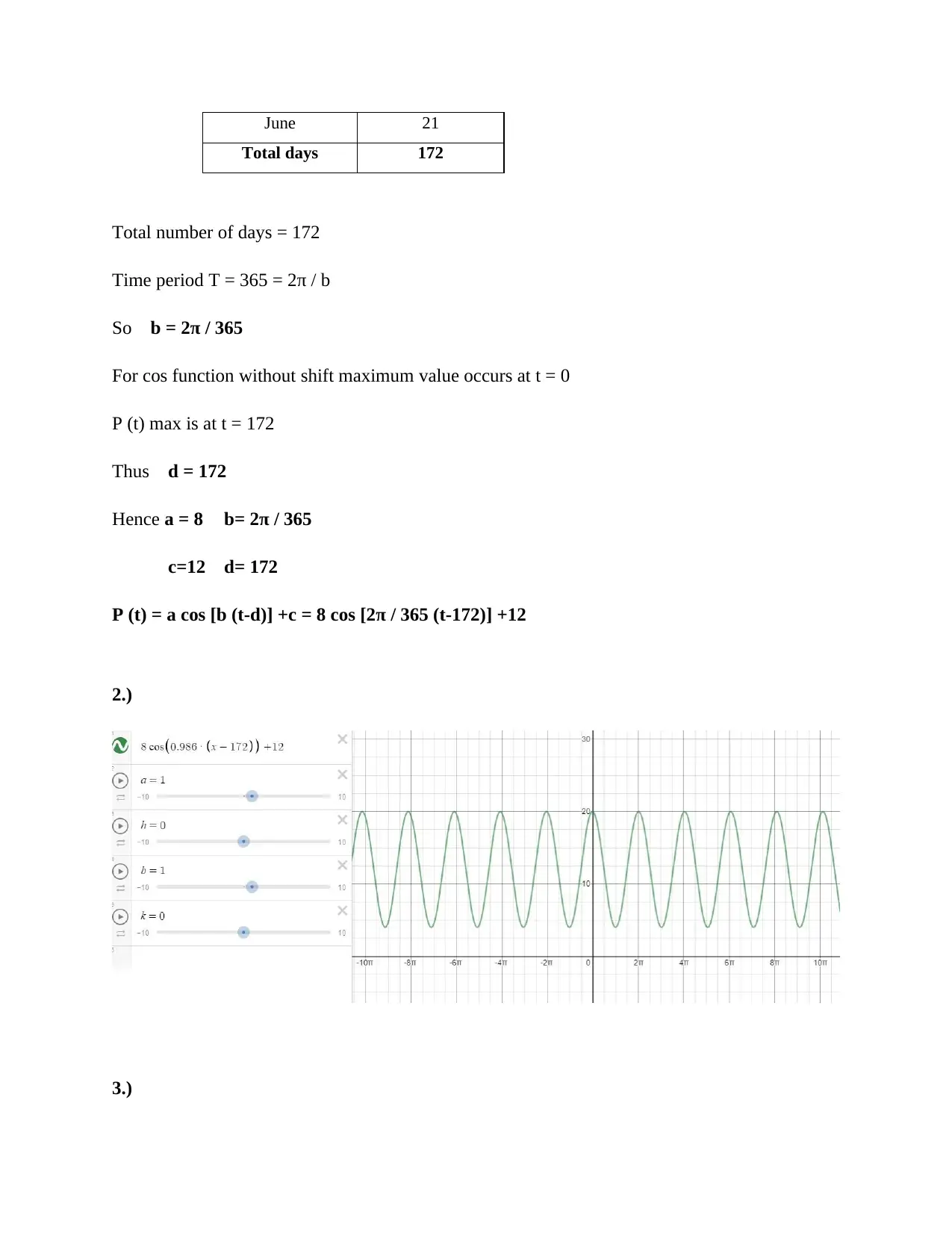
June 21
Total days 172
Total number of days = 172
Time period T = 365 = 2π / b
So b = 2π / 365
For cos function without shift maximum value occurs at t = 0
P (t) max is at t = 172
Thus d = 172
Hence a = 8 b= 2π / 365
c=12 d= 172
P (t) = a cos [b (t-d)] +c = 8 cos [2π / 365 (t-172)] +12
2.)
3.)
Total days 172
Total number of days = 172
Time period T = 365 = 2π / b
So b = 2π / 365
For cos function without shift maximum value occurs at t = 0
P (t) max is at t = 172
Thus d = 172
Hence a = 8 b= 2π / 365
c=12 d= 172
P (t) = a cos [b (t-d)] +c = 8 cos [2π / 365 (t-172)] +12
2.)
3.)

P (t) = 8 cos [2π / 365 (t-172)] +12
P min =4
Thus
4 = 8 cos [2π / 365 (t-172)] +12
8 cos [2π / 365 (t-172)] = -8
cos [2π / 365 (t-172)] = -1
t = 354.5 days = first 11 months
Thus minimum power is produced by solar system on 354.5 th day which is on 21 December
4.)
Power produced > = 16 kwh/ day
P (t) = 8 cos [2π / 365 (t-172)] +12 = 16
8 cos [2π / 365 (t-172)] = 4
cos [2π / 365 (t-172)] = 0.5
t = 232.8
as t > 172 which is t for maximum power
t1 = 172 – (232.8 - 172) = 111.2
t2 – t1 = 232.8 – 111.2
t2 – t1 = 121.6 days
Thus the power produced by system is sufficient for 121.6 days.
P min =4
Thus
4 = 8 cos [2π / 365 (t-172)] +12
8 cos [2π / 365 (t-172)] = -8
cos [2π / 365 (t-172)] = -1
t = 354.5 days = first 11 months
Thus minimum power is produced by solar system on 354.5 th day which is on 21 December
4.)
Power produced > = 16 kwh/ day
P (t) = 8 cos [2π / 365 (t-172)] +12 = 16
8 cos [2π / 365 (t-172)] = 4
cos [2π / 365 (t-172)] = 0.5
t = 232.8
as t > 172 which is t for maximum power
t1 = 172 – (232.8 - 172) = 111.2
t2 – t1 = 232.8 – 111.2
t2 – t1 = 121.6 days
Thus the power produced by system is sufficient for 121.6 days.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

D.
Vector P = 4i +0j + 7k
Vector q = -2i + j + 3k
Solution
Dot product between two vectors is given by the formula:
p.q = |p| |q|. Cos ϴ
p.q = (4i +0j + 7k). (-2i + j + 3k) = 13
|p| = √65
|q| = √14
13 = √65 * √14 Cos ϴ
Cos ϴ = 13
ϴ = 64.47 degree = 1.12 radian
E.
Solution
Sin (a + b) = sin a cos b + cos a sin b
Sin (x + π) = sin x cos π + cos x sin π
Sin π = 0 and cos π = -1
Sin (x + π) = - sin x
Similarly
Sin (a - b) = sin a cos b - cos a sin b
Sin (x - π) = sin x cos π - cos x sin π
Vector P = 4i +0j + 7k
Vector q = -2i + j + 3k
Solution
Dot product between two vectors is given by the formula:
p.q = |p| |q|. Cos ϴ
p.q = (4i +0j + 7k). (-2i + j + 3k) = 13
|p| = √65
|q| = √14
13 = √65 * √14 Cos ϴ
Cos ϴ = 13
ϴ = 64.47 degree = 1.12 radian
E.
Solution
Sin (a + b) = sin a cos b + cos a sin b
Sin (x + π) = sin x cos π + cos x sin π
Sin π = 0 and cos π = -1
Sin (x + π) = - sin x
Similarly
Sin (a - b) = sin a cos b - cos a sin b
Sin (x - π) = sin x cos π - cos x sin π
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Sin (x - π) = - sin x
Thus Sin (x - π) = Sin (x + π)
G.
Sin a = 3/5
Sin b = 5/13
Solution
Sin (a + b) = sin a cos b + cos a sin b
Sin2 ϴ + cos2 ϴ = 1
cos2 a = 1 - Sin2 a
cos2 a = 1 – (3/5) 2 = 0.64
cos a = 0.8
Similarly
cos2 b = 1 – (5/13) 2 = 0.92
cos b = 0.92
sin (a +b) = (3/5) * 0.92 + (0.64*(5/13))
= 0.798
Sin (a + b) = 0.798
Thus Sin (x - π) = Sin (x + π)
G.
Sin a = 3/5
Sin b = 5/13
Solution
Sin (a + b) = sin a cos b + cos a sin b
Sin2 ϴ + cos2 ϴ = 1
cos2 a = 1 - Sin2 a
cos2 a = 1 – (3/5) 2 = 0.64
cos a = 0.8
Similarly
cos2 b = 1 – (5/13) 2 = 0.92
cos b = 0.92
sin (a +b) = (3/5) * 0.92 + (0.64*(5/13))
= 0.798
Sin (a + b) = 0.798

⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 16
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





