Engineering Maths Assignment: Statistical Analysis and Probability

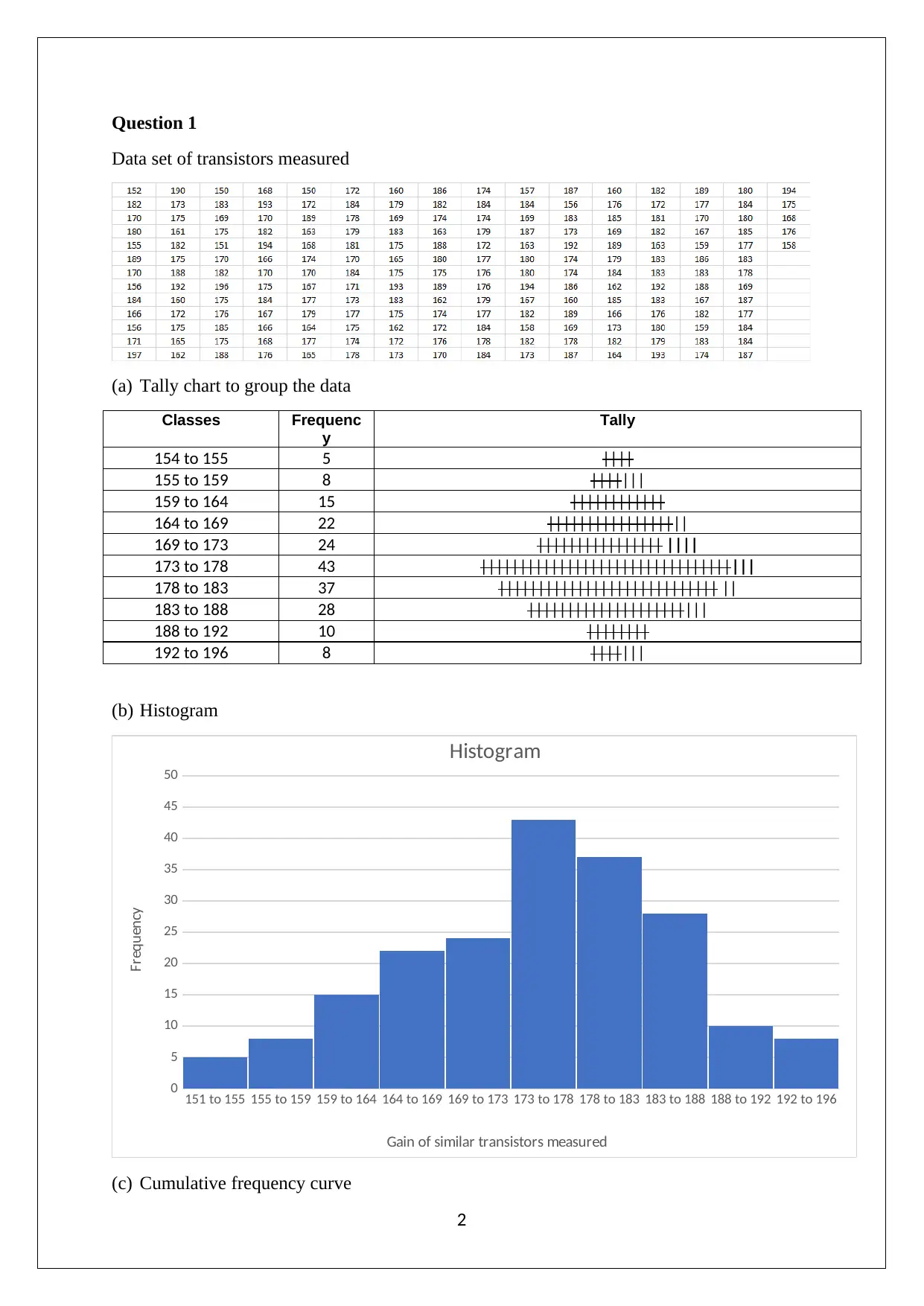
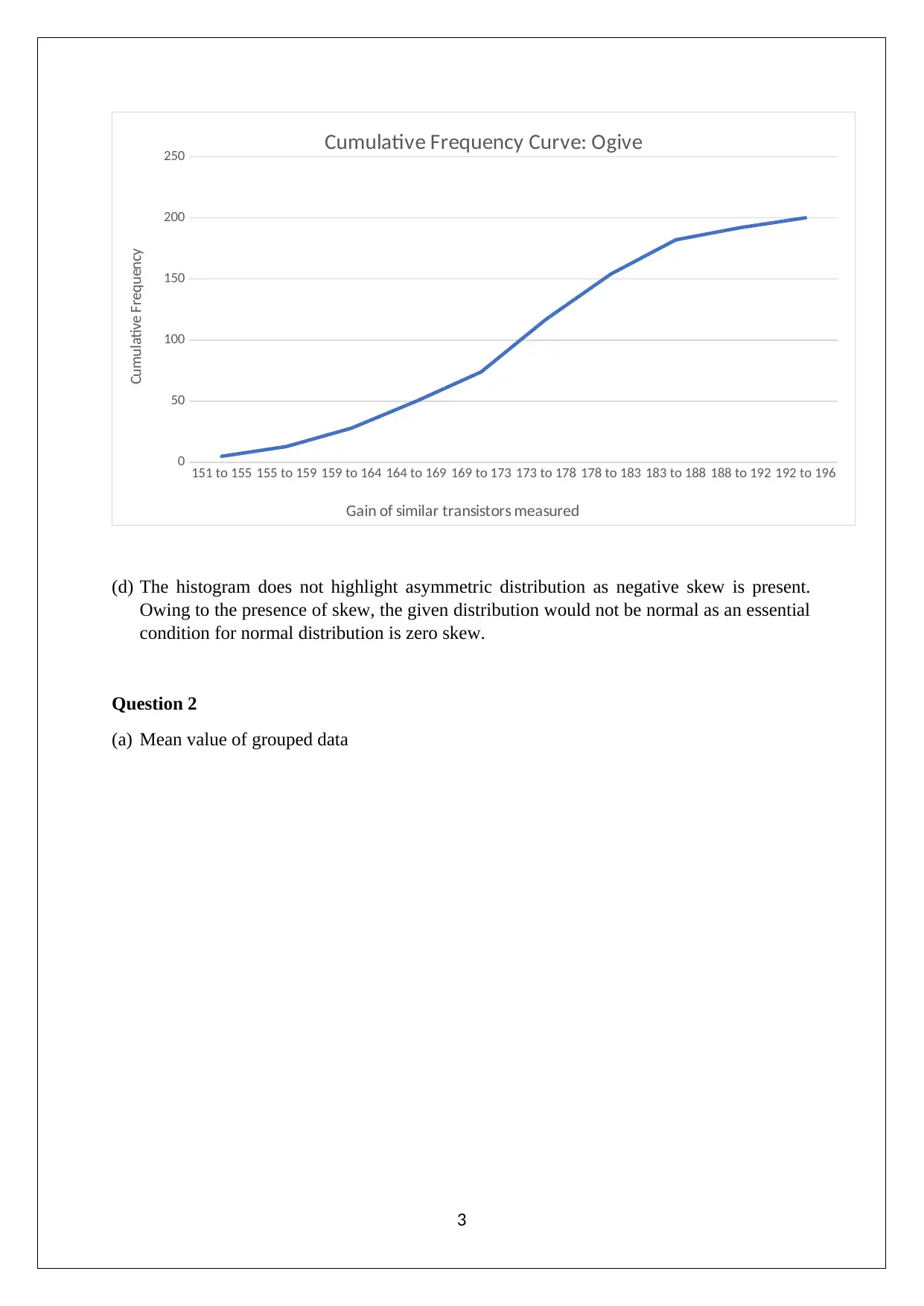
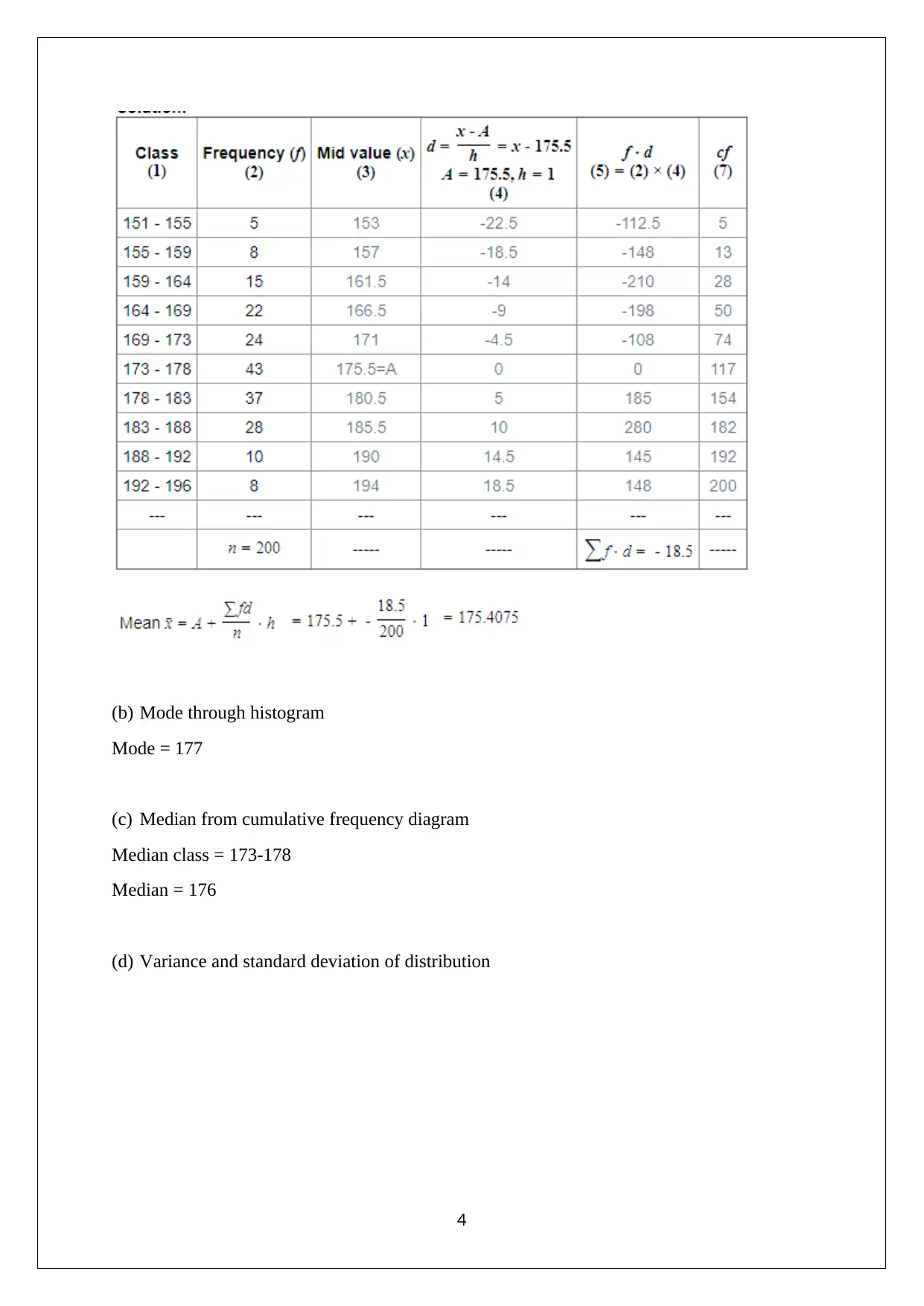
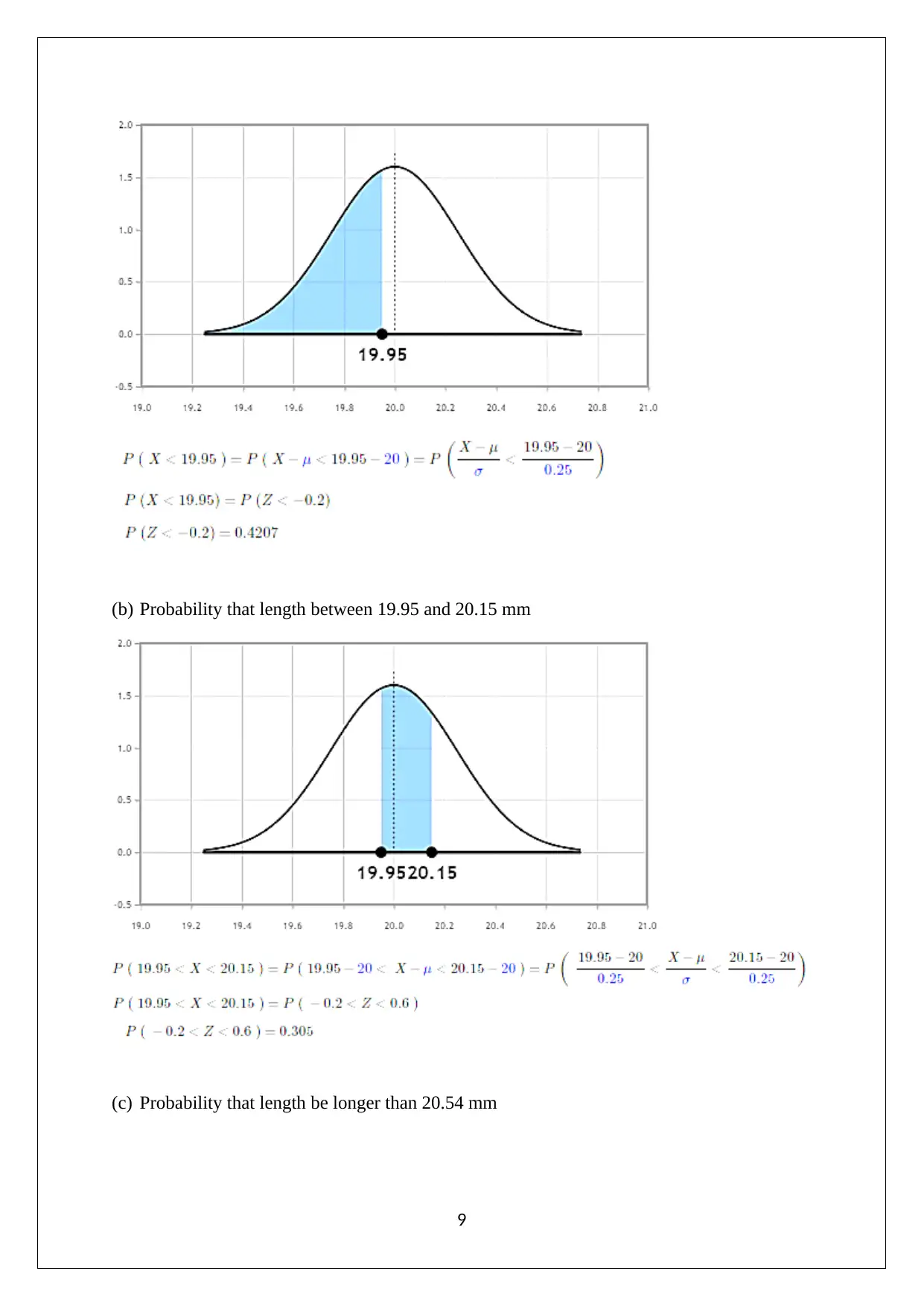
This Engineering Maths assignment solution analyzes a dataset of transistors, presenting a tally chart, histogram, and cumulative frequency curve to visualize the data distribution. It calculates the mean, mode, and median, and explores the variance and standard deviation. The assignment further investigates the relationship between tensile force and extension using a scatter plot and regression equation, determining the correlation coefficient. Finally, it delves into probability calculations using a normal distribution, determining the probability of bolt lengths falling within specific ranges and calculating confidence limits for the average bolt length. This comprehensive solution is designed to aid students in understanding and applying statistical concepts within an engineering context.

ENGINEERING MATHS
STUDENT ID:
[Pick the date]

Question 1
Data set of transistors measured
(a) Tally chart to group the data
Classes Frequenc
y
Tally
154 to 155 5 ||||
155 to 159 8 |||||||
159 to 164 15 ||||||||||||
164 to 169 22 ||||||||||||||||||
169 to 173 24 |||||||||||||||| ||||
173 to 178 43 |||||||||||||||||||||||||||||||||||
178 to 183 37 |||||||||||||||||||||||||||| ||
183 to 188 28 |||||||||||||||||||||||
188 to 192 10 ||||||||
192 to 196 8 |||||||
(b) Histogram
151 to 155 155 to 159 159 to 164 164 to 169 169 to 173 173 to 178 178 to 183 183 to 188 188 to 192 192 to 196
0
5
10
15
20
25
30
35
40
45
50
Histogram
Gain of similar transistors measured
Frequency
(c) Cumulative frequency curve
2

151 to 155 155 to 159 159 to 164 164 to 169 169 to 173 173 to 178 178 to 183 183 to 188 188 to 192 192 to 196
0
50
100
150
200
250 Cumulative Frequency Curve: Ogive
Gain of similar transistors measured
Cumulative Frequency
(d) The histogram does not highlight asymmetric distribution as negative skew is present.
Owing to the presence of skew, the given distribution would not be normal as an essential
condition for normal distribution is zero skew.
Question 2
(a) Mean value of grouped data
3

(b) Mode through histogram
Mode = 177
(c) Median from cumulative frequency diagram
Median class = 173-178
Median = 176
(d) Variance and standard deviation of distribution
4

Question 3
5

(a) Scatter plot
(b) Regression equation
6

Extension (nm) = 0.96609 + (0.74805*Tensile Force(kN))
Question 4
Correlation coefficient
7

The correlation coefficient comes out to be 0.9918.
Question 5
Average length of bolts = 20 mm
Standard deviation = 0.25 mm
Sample size = 500
Normal distribution
(a) Probability that length of less than 19.95 mm
8

(b) Probability that length between 19.95 and 20.15 mm
(c) Probability that length be longer than 20.54 mm
9

(d) Number of bolts = 15
Actual length of bolt for 90% confidence limits
Degree of freedom = 15-1= 14
Standard error = standard deviation/ sqrt (15) = 0.25/ sqrt (15) = 0.0645
The t value for 90% confidence limit = 1.76
Margin of error = t value * standard error = 0.0645 * 1.76 = 0.113691
Lower limit = Average - Margin of error = 20 – 0.113691 = 19.8864
Upper limit = Average + Margin of error = 20 + 0.113691 = 20.1136
Hence, it can be said with 90% confidence that the mean length of bolt would fall between
19.8864 and 20.1136.
10