University Engineering Modeling and Simulation Homework Assignment

This document presents a comprehensive solution to an engineering modeling and simulation assignment. It includes MATLAB code and outputs for several tasks, such as finding integer solutions to a quadratic equation, calculating the value of 'g' based on velocity and radius of curvature, simulating contamination of ponds using differential equations, determining the natural frequency of a vibrating system using mass and stiffness matrices, calculating the range of a projectile in both ideal and air resistance scenarios. The solutions cover a range of engineering concepts, including dynamics, projectile motion, and system analysis, providing a detailed understanding of the problem-solving process using MATLAB.

Running head: MODELLING AND SIMULATION OF ENGINEERING
MODELLING AND SIMULATION OF ENGINEERING
Name of the Student
Name of the University
Author Note

2MODELLING AND SIMULATION OF ENGINEERING
Task 1:
MATLAB code:
%% s3761924
c = 2029;
a = 1;
b = sqrt(c^2 - a^2);
while mod(b,1) ~= 0
b = sqrt(c^2 - a^2);
a = a+1;
end
sprintf('The value of a is %d and the value of b is %d',a-1,b)
Output:
task1
ans =
'The value of a is 180 and the value of b is 2021'
Task 2:
MATLAB code:
%% s3761924
% vx = v*cos(theta), vy = v*sin(theta) => v = sqrt(vx^2 + vy^2)
vx = -9.2; % vx = -9.2 m/s

3MODELLING AND SIMULATION OF ENGINEERING
vy = -4.2; % vy = -4.2 m/s
v = -sqrt(vx^2 + vy^2);
theta = acosd(vx/v); % vx = v*cos(theta) => theta = acos(vx/v)
R = 995; % radius of curvature R = 995 m
g = ((v^2)/R)*cosd(theta); % (mv^2/R)*cos(theta) = m*g (centripetal force = centrifugal
force)
sprintf('the value of g is %.3f m/s^2',g)
Output:
task2
ans =
'the value of g is 0.094 m/s^2'
Task 3:
MATLAB code:
% dx3/dt = f3 + (f23/V2)*x2(t); dx4/dt = f4+(f34/V3)*x3(t)+(f24/V2)*x2(t); dx1/dt =
(f41/V4)*x4(t);
% dx2(t)/dt = (f12/V1)*x1(t)
f3 = 1; % in 1 kg/h
f4 = 3.1; % in 3.1 kg/h
% forming the set of differential equations

4MODELLING AND SIMULATION OF ENGINEERING
odes = @(t,x)[0.05*x(4);0.05*x(1);f3 + 0.02*x(2) + 0.03*x(3);f4 + 0.03*x(4)];
%(f23/V2)=(f34/V3)=0.02,(f24/V2)=0.03,(f12/V1) = (f41/V4) = 0.05
[t,x] = ode45(odes,[0 48],[0 0 0 0]); % initial values are 0 as ponds are prestine initially and
the time is 0 to 48 hours
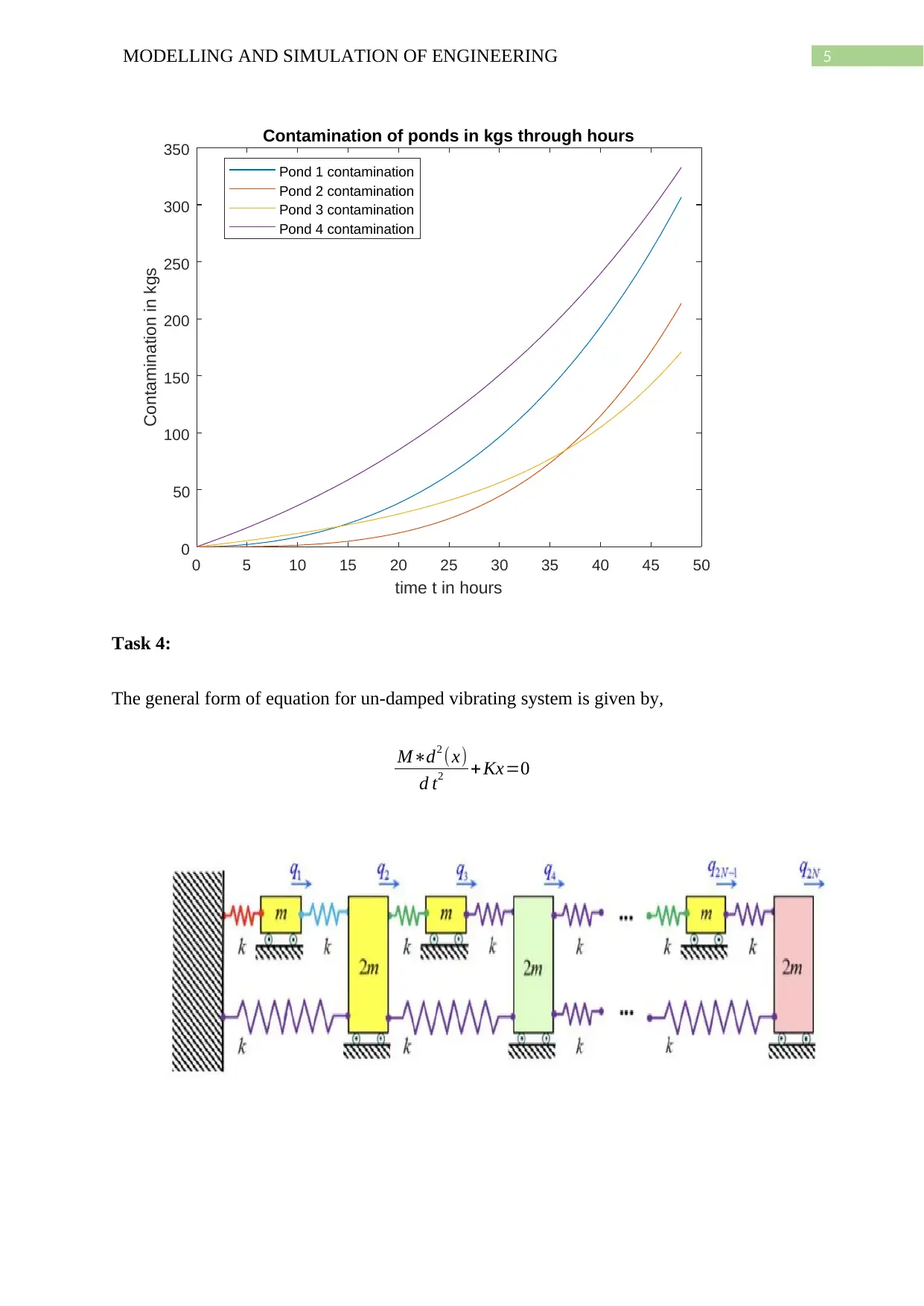
plot(t,x(:,1),t,x(:,2),t,x(:,3),t,x(:,4))
title('Contamination of ponds in kgs through hours')
xlabel('time t in hours')
ylabel('Contamination in kgs')
legend('Pond 1 contamination','Pond 2 contamination','Pond 3 contamination','Pond 4
contamination')
sprintf('the contamination of pond 1 at the end of 48 hours will be %d',round(x(end,1)))
Output:
task3
ans =
'the contamination of pond 1 at the end of 48 hours will be 307'

5MODELLING AND SIMULATION OF ENGINEERING
0 5 10 15 20 25 30 35 40 45 50
time t in hours
0
50
100
150
200
250
300
350
Contamination in kgs
Contamination of ponds in kgs through hours
Pond 1 contamination
Pond 2 contamination
Pond 3 contamination
Pond 4 contamination
Task 4:
The general form of equation for un-damped vibrating system is given by,
M∗d2 (x)
d t2 + Kx=0

6MODELLING AND SIMULATION OF ENGINEERING
Now, M and K matrix will be N*N dimensional as there are total of M masses and
corresponding k’s. Here, N=50. The M and K matrixes are constructed in MATLAB as given
below.
MATLAB code:
%% s3761924
M = zeros(50); K = zeros(50);
m = 7; % mass 7 kg
k = 1e4; % spring constant 10000 N/m
% Contructing the Mass matrix M
for i =1:length(M)
M(i,i) = 2*m;
end
for i=1:length(M)
for j=1:length(M)
if M(i,j) == 0
M(i,j) = m;
end

7MODELLING AND SIMULATION OF ENGINEERING
end
end
% Constructing the K matrix
for i=1:length(K)
K(i,i) = (50-1)*k;
end
for i=1:length(K)
for j=1:length(K)
if K(i,j) == 0
K(i,j) = -48*k; % kij = -k - k ...48 terms when i not equal to j
end
end
end
lambda = eig(K,M);
omega_3 = sqrt(lambda(3)); % omega(i) = sqrt(lambda(i)) where omega(i) = ith natural
frequency of the system.
sprintf('Hence the 3rd naural frequency of the system is Omega_3 = %.4f Hz',omega_3)

8MODELLING AND SIMULATION OF ENGINEERING
Output:
task4
ans =
'Hence the 3rd natural frequency of the system is Omega_3 = 372.2518 Hz'.
Question 5:
m = 2 kg, g = 9.8 m/s^2, inclination angle theta = 30 degrees.
Height of fall Z = 3 meters.
Now, the velocity of the object will be determined from the following equation. Initial
velocity = 0 m/s of the mass.
v^2 = u^2 + 2*f*s
 v = sqrt(u^2 + 2*f*s) = sqrt(2*9.8*3) = 7.6681 m/sec.
Now, as the collision is perfect and no energy loss, hence, the speed will be same after the
collision. Hence, initial speed through the inclined projectile is v = 7.6681 m/sec.
The range of flight (the distance BC) is calculated in MATLAB by the following formula.
R=
( v2
gco s2 ( α ) )∗( sin ( 2θ +α )+ sinα )
Here, by geometry θ = α = 30 degrees.
MATLAB code:
%% s3761924
m = 2; % kg
g = 9.8; % m/s^2

9MODELLING AND SIMULATION OF ENGINEERING
alpha = 30; % inclination angle in degrees
theta = 30; % launch angle from horizontal
Z = 3; % release height 3 meter
u = 0; % object is rest before relasing from top
v = sqrt(u^2 + 2*g*Z);
R = (v^2/(g*cosd(alpha)^2))*(sind(2*theta + alpha) + sind(alpha));
sprintf('The range of flight BC is %.2f meters',R)
Output:
task5
ans =
'The range of flight BC is 12.00 meters'
Question 6:
Now, the air resistance force is proportional to square of velocity of mass.
F=Cd∗v2
MATLAB code:
%% s3761924
m = 2; % kg
g = 9.8; % m/s^2
alpha = 30; % inclination angle in degrees
theta = 30; % launch angle from horizontal

10MODELLING AND SIMULATION OF ENGINEERING
Z = 3; % release height 3 meter
u = 0; % object is rest before relasing from top
Cd = 0.3; % coefcient of air resistance force
v = sqrt(u^2 + 2*g*Z);
f_air = (Cd*v^2)/m; % air resitance retardation
v = sqrt(u^2 + 2*(g-f_air)*Z); % finding net velocity before hitting the inlcined surface
R = (v^2/(g*cosd(alpha)^2))*(sind(2*theta + alpha) + sind(alpha)); % range of flight in
inclined plane
sprintf('The range of flight BC is %.2f meters',R)
Output:
task6
ans =
'The range of flight BC is 1.20 meters'