Wheel Analysis and Gyroscopic Precession: Engineering Project

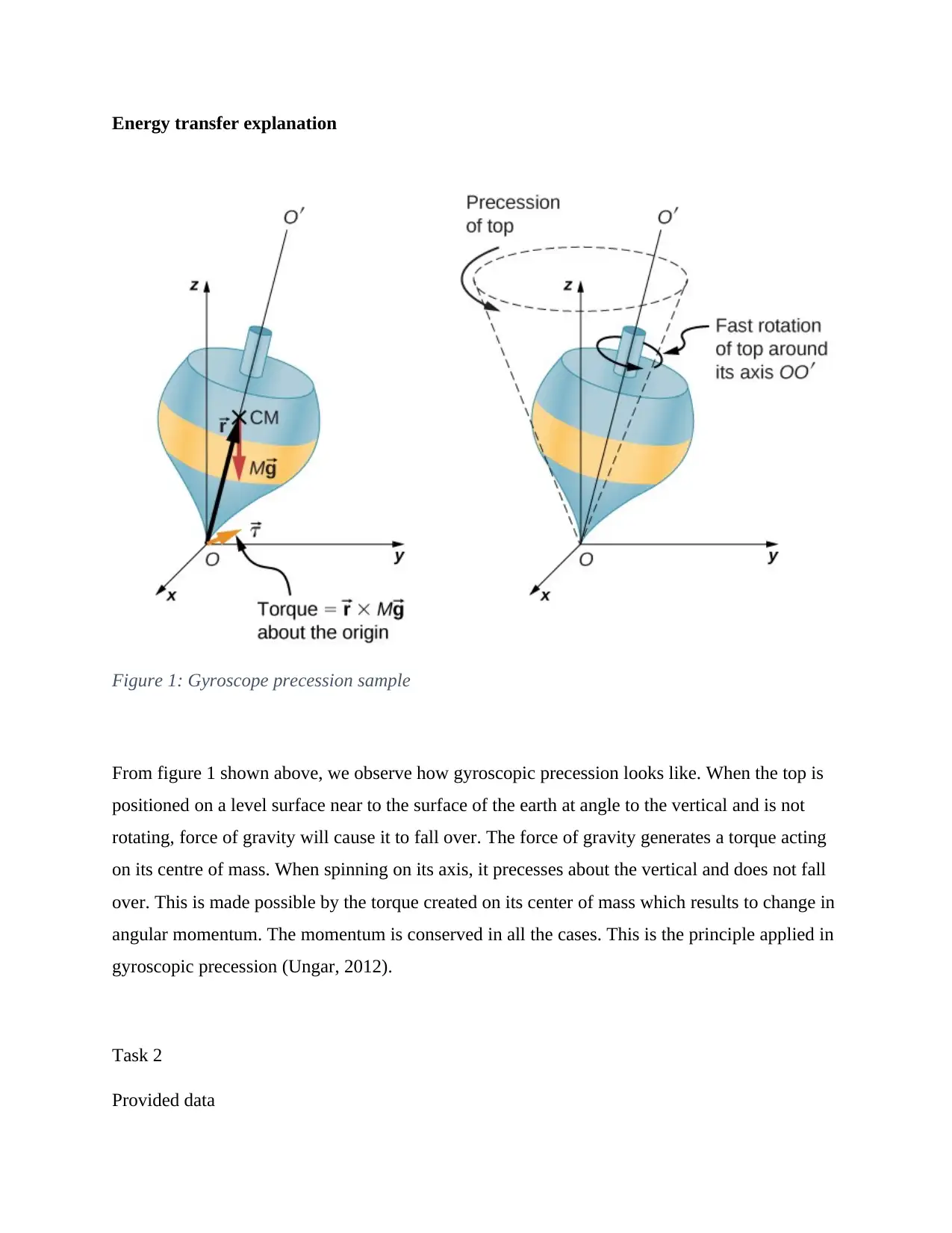
This mechanical engineering project involves a detailed analysis of a wheel's properties, including the calculation of mass, angular momentum, and torque. The project utilizes provided data such as the radius, time, and angular velocity to determine the wheel's characteristics. The solution also explores the concept of gyroscopic precession, explaining the principles behind it using a diagram and the application of a free body diagram. Furthermore, the project extends to the analysis of a crankshaft, presenting vector diagrams and calculations for velocity and acceleration. References to relevant research papers are also included, providing a comprehensive understanding of the concepts covered in the project.

Task 1
Part 1
Provided Data:
Radius of the wheel rim R = 0.6 m
Torque (τ ) required to spin the wheel = 4 Nm
Time taken (t) to spin the wheel from rest to final velocity = 24 seconds
Final angular velocity (ω2 ¿ = 27 rad/s
Moment of inertia = m R2
Distance from chain to centre of wheel = 0.12 m
Required: Mass of the wheel, angular momentum and axial torque in the system.
Solution
Torque = Force * Radius
τ =FR
F= τ
R = 4
0.6 =6.6667 N
Angular acceleration α = ω2−ω1
∆ t
α= 27−0
24 =1.125 rad /s2
Force F=mRα
Making m the subject;
m= F
Rα = 6.6667
0.6∗1.125 =9.877 kg
Therefore, the mass of the wheel is 9.877 kg.

Angular momentum L=Iω
Moment of inertia I =m R2
I =9.877∗0.62=3.5556 kg m2
ω=27 rad / s
Substituting in the formula, we get;
L=3.5556∗27=96 kg m2 / s
Thus, the angular momentum is 96 kg m2 / s
Torque on the axle producing the gyroscopic perception is given by;⃗
τ =⃗ r m⃗ g
Where;⃗
r =0.12 m
m=9.877 kg⃗
g=9.8 m/s2
Substituting back;⃗
τ =0.12∗9.877∗9.81=11.627 Nm⃗
τ =11.627 Nm

Energy transfer explanation
Figure 1: Gyroscope precession sample
From figure 1 shown above, we observe how gyroscopic precession looks like. When the top is
positioned on a level surface near to the surface of the earth at angle to the vertical and is not
rotating, force of gravity will cause it to fall over. The force of gravity generates a torque acting
on its centre of mass. When spinning on its axis, it precesses about the vertical and does not fall
over. This is made possible by the torque created on its center of mass which results to change in
angular momentum. The momentum is conserved in all the cases. This is the principle applied in
gyroscopic precession (Ungar, 2012).
Task 2
Provided data

l1=70 mm
l2=250 mm
α=600
ω=240 rad / s
Solution
i) Free body diagram
a) Tangential velocity V tBA=ωr=240∗0.07=16.8 m/s
b) Vector diagram
By geometry, V CB=8.4 m/ s
c) From the vector diagram and use of geometry, V CA=14.549 m/s (Tanik, 2011)
d) Centripetal acceleration α BA = v2
r =16.82
0.07 =4032rad /s2

e) Centripetal acceleration α CB= v2
r = 8.42
0.25 =282.24 rad / s2
f) Acceleration diagram
α piston=846.693 rad /s2
ii) Crankshaft
(V B)A =ωr=366∗0.011=4.026 m/s
The vector diagram will be as below;

From the diagram, velocity of the piston will be 2.847 m/s
Centripetal acceleration of B relative to A = ω2 x=3662∗0.011=1473.516 m/ s2
Centripetal acceleration of C relative to B ¿ v2
BC = 2.8472
0.05 =162.108 m/s2
The centripetal diagram will be as shown below.
Thus the acceleration of the piston will be 489 m/ s2
iii)Using trigonometric equations
For part (i), linear velocity V =l1∗ω∗cos α
V =0.07∗240∗cos 600=8.4 m/ s
Linear acceleration a= V 2
r = 8.42
0.07 =1008 m/ s2
For part (ii), linear velocity V =0.011∗ω∗cos α
V =0.011∗366∗cos 450=2.847 m/ s
Linear acceleration a= V 2
r = 2.8472
0.011 =736.758 m/s2

References
Tanik, E., 2011. Transmission angle in compliant slider-crank mechanism. Mechanism and
Machine Theory, 46(11), pp.1623-1632.
Ungar, A.A., 2012. Beyond the Einstein addition law and its gyroscopic Thomas precession: The
theory of gyrogroups and gyrovector spaces (Vol. 117). Springer Science & Business Media, pp
32-67.