University Assignment: Numerical Solutions for Balancing and Vibration

This document presents detailed solutions to numerical problems related to balancing and vibration, covering topics such as single-plane balancing, multiple-plane balancing, crankshaft balancing, and the analysis of vibrating systems. The solutions include step-by-step calculations, vector analysis, and free body diagrams to illustrate the concepts. Problem 1 addresses the balancing of an unbalanced flywheel by determining the magnitude and angular position of a balancing weight. Problem 2 focuses on balancing masses in multiple planes on a shaft supported by bearings. Problem 3 analyzes the balancing of a crankshaft with reciprocating pistons, and Problem 4 provides an analysis of a two-mass vibrating system. The document provides a comprehensive understanding of balancing and vibration principles through these worked examples.

Balancing and Vibration

Numerical on Balancing and Vibration
Contents
Solution -1.......................................................................................................................................3
Solution -2.......................................................................................................................................4
Solution -3.......................................................................................................................................6
Solution -4.....................................................................................................................................10
a)................................................................................................................................................10
b)................................................................................................................................................12
c)................................................................................................................................................13
1 | P a g e

Numerical on Balancing and Vibration
Solution -1
The given problem statement describe the balancing in one plane,
The balancing of single plane can be done in following ways
The given amplitude = 0.165 mm at an angle = 15o clockwise.
Required mass = 50 gm at an angle 45o CCW and amplitude 0.225 mm.
For solving this problem, first we must convert all polar vectors into rectangular vector form.
Let the vector of required mass = ⃗ V u ⃗
V u=0.165←15o = = 0.165*Cos (-15o) +0.165*Sin (-15o) = 0.16 - 0.0427j
The calculated vector of trial weight, ⃗ V u +w⃗
V u +w=0.225< 35o = 0.18431+0.130j
Now required weight vector⃗
W w=50< 45o = 35.36 + 35.36j
We can present the required vector in the following way⃗
V u=⃗ A A⃗ W w …………. (i)⃗
V u +w=⃗ A A (⃗ W w+⃗ W w) …………. (ii)
From above equation, we must subtract (i) from (ii)⃗
A A=⃗ V u+ w−⃗ V u⃗
W w
¿ [ 0.184+0.130 j ]− [ 0.16−0.0427 j ]
35.36+35.36 j =( 0.024+0.176 j)
35.36+35.36 j =
(−0.024 +0.176 j)(35.36−35.36)
( 35.36+35.36 ) 35.36−35.36 ¿ ¿= 6.72−5.304 j
2500.659
= 0.0024+0.17271j
This is the required vector ⃗ A A now we must calculate⃗ W u, with following mathematical condition.
2 | P a g e

Numerical on Balancing and Vibration⃗
W u=⃗ V u+w⃗
AA
−⃗ W w
If we present the values in above equation
¿ [ 0.184+0.130 j ]
0.0024+0.17271 j −35.36+35.36 j
= -6.15-2.0812j
Now the required vector is calculated, to make the wheel balanced, we must place this mass in
opposite direction of wheel
i.e. ⃗ B=−⃗ W u
Or⃗ B=6.15+2.0812 j
The vector in polar form is given as⃗
B❑=6.49< 18.67oCCW.
As the result above calculated, we must put the mass of 6.49 gm at 18.67o CCW
Solution -2
There is mass of 1 kg, 3 kg and 2 kg, are in the radius of 50, 75 and 25 mm, in the planes C, D,
and E, the support bearing is at the place B, and F. This is the case of multiple plane balancing.
As the
condition
above
described,
We must
calculated the
mass and
radius in plane A,G. Taking G as the reference plane, we must calculate all the distances
lf =200 mm
3 | P a g e

Numerical on Balancing and Vibration
lE =600 mm
lD =1200 mm
lC=2000 mm
lB =2200 mm
lA =2600 mm
The weight vector, for given mass can be represented as given below⃗
W C=1<90o⃗
W D =3<220o⃗
W E =2<330o
Calculating the all radius position as per reference plane radius position
W c
' = rc
R x⃗ WC= 50
50∗1=1Mass as per new weight vectorW c
' =1< 90o, with predefined
reference plane of 50 mm
W D
' = r D
R x⃗ W D= 75
50∗3=1Mass as per new weight vectorsW c
' =4.5<220o, with predefined
reference plane of 50 mm radius
W E
' = r E
R x⃗ WE = 25
50∗2=1 Mass as per new weight vectors W c
' =1<330o, with predefined
reference plane of 50 mm
As per new weight vector, we must convert all polar vectors into rectangular form
Polar vector ofW AC
' =1< 90o, will be 0+ 0.77j with predefined reference plane of 50 mm
Polar vector ofW AD
' =4.5<220o, will be -1.59 - 1.34j with predefined reference plane of 50 mm
Polar vector ofW AE
' =1< 330o, will b0.2 -0.12j with predefined reference plane of 50 mm
The total unbalance weight in rectangular form = -1.39-0.69j.
The required vector from above result = ⃗ W A =⃗ W AC+⃗ W AE +⃗ W AD
The required weight at position A in rectangular form = -1.39-0.69j or 1.552<206.39o Ans
4 | P a g e

Numerical on Balancing and Vibration
Similarly, we must calculate unbalance weight in plane G
W GC
' =lA −lC
l A
x⃗ W ' C= 2600−2000
2600 ∗1=0.2301 Mass as per new weight vector W c
' =0.2301<90o, or
(0, 0.23j) with predefined reference plane of 50 mm
W GD
' =lA −lD
l A
x⃗ W 'D = 2600−1200
2600 ∗4.5=2.423 Mass as per new weight vector W c
' =2.423<220o,
or (-1.86, -1.56j) with predefined reference plane of 50 mm
W ¿
' = l A−lE
lA
x⃗ W 'E = 2600−600
2600 ∗1=0.231 Massas per new weight vector W c
' =0.77<330o,
or (0.67, -.39j) with predefined reference plane of 50 mm Total unbalance vector =⃗
W G=⃗ W GC+⃗ W ¿+⃗ W GD⃗
W G=¿-1.19-1.72j or 2.09<23532 at radius 50 mm
Therefore, required weight at A = 1.552 kg and at G = 2.09 kg at a radius of 50 mm Ans
Solution -3
As per the
question described, this is the free body diagram of crank shaft its each piston is separated by fix
distance in axial direction, and constant angular position.
α 1=a6=0o , a2=a5 =120o , a3=a4=240o,
The length is represented as r, The connecting rod is represented by l, reciprocating mass is
represented by m, and rotating mass = mC Cylinder 1 is taken as reference plane.
5 | P a g e

Numerical on Balancing and Vibration
l1=0 m
Distance for reciprocating cylinder 2 = l2=a
Distance for reciprocating cylinder 3 = l3=2 a
Distance for reciprocating cylinder 4 = l4 =3 a
distance for reciprocating cylinder 5 = l5=4 a
distance for reciprocating cylinder 6 = l6=5 a
The angular velocity = ω
The forces acting in x,y, and z direction can be given as
( Fx )i= ( m+ mc ) r ω2 cos ( ωt+ αi ) +m r 2 ω2
l cos (2 ωt+ 2αi) ……(i)
The x component of all forces in x direction
( Fx )total= ( m+ mc ) r ω2
∑
i=1
N
cos ( ωt+ αi ) + m r2 ω2
l ∑
i=1
N
cos (2 ωt +2 αi )… … (ii)
Similarly, the x and y component of all forces in y direction
( F y )total=−(mc)r ω2
∑
i=1
N
sin ( ωt +αi ) …………(iii)
For the pupose of simplifying the equation we must take. t = 0
The variable is given as follows
∑
i=1
N
cos (ωt +α i ), ∑
i=1
N
cos (2 ωt+ 2 αi ), ∑
i=1
N
sin ( ωt+αi )
For equation,
∑
i=1
N
cos (ωt +α i )=∑
i=1
N
cos ( 0 t+ αi ) =∑
i=1
N
cos ( αi )
⟹∑
i=1
N
cos ( αi )=cos ( α 1 ) +cos ( α2 ) +cos ( α3 ) +cos ( α 4 ) +cos ( α5 ) + cos ( α 6 )
6 | P a g e

Numerical on Balancing and Vibration
Putting the value of a1=a6 =0o , a2=a5 =120o , a3=a4=240o,
⟹∑
i=1
N
cos ( αi )=cos ( 0o ) +cos ( 120o ) + cos ( 240o )+cos ( 240o )+ cos ( 120o ) + cos ( 0o )=1−0.5−0.5−0.5−0.5+1=0
The trigonometrical value,∑
i=1
N
cos ( 2 ωt+ 2 αi ), Putting the α value and t = 0
∑
i=1
N
cos (2 ωt+ 2 αi )=cos ( 2∗0o ) +cos ( 2∗12 0o ) + cos ( 2∗24 0o ) +cos ( 2∗24 0o ) +cos ( 2∗12 0o ) + cos ( 2∗0o )=1−0.5−0.5
For equation ∑
i=1
N
sin ( ωt+αi ) =∑
i=1
N
sin ( 0 t +α i )=∑
i=1
N
sin ( αi )
∑
i=1
N
sin ( αi ) =sin ( αi ) +sin ( α2 )+ sin ( α 3 )+sin (α 4 ) +sin ( α5 ) +sin ( α6 )
∑
i=1
N
sin ( αi ) =sin ( αi ) +sin ( α 2 )+ sin ( α 3 )+ sin (α4 ) +sin ( α5 ) +sin ( α6 )
Putting the value of a1=a6 =0o , a2=a5 =120o , a3=a4=240o,
∑
i=1
N
sin ( αi ) =sin ( 0o ) + sin ( 120o ) +sin ( 240o ) +sin ( 240o ) + sin ( 120o ) +sin ( 0o )
∑
i=1
N
sin ( αi ) =0+ √3
2 − √3
2 − √3
2 + √ 3
2 +0 = 0
Putting the required value in equation (ii)
( Fx ) total= ( m+mc ) r ω2
∑
i=1
N
cos ( ωt+ αi ) + m r2 ω2
l ∑
i=1
N
cos (2 ωt +2 αi )
( Fx )total= ( m+ mc ) r ω2 xo+m r 2 ω2
l x 0=0
Replacing the required value from trigonometry (iii)
7 | P a g e

Numerical on Balancing and Vibration
( F y )total=− ( mc ) r ω2
∑
i=1
N
sin (ωt + αi )=¿− ( mc ) r ω2 ( 0 ) =0
We can see that, the sum of unbalance forces in x and y direction is 0
( Fx )total=0
( F y )total=0
Calculating the moment about z axis
M z =∑
i=0
N
( Fx )i li
From equation (i)
M z = ( m+mc ) r ω2
∑
i =1
N
cos ( ωt +αi ) +m r2 ω2
l ∑
i=1
N
cos (2ωt +2 αi) x li ……(iv)
Calculating the moment about z axis
M x=∑
i =0
N
( Fx )i li From equation (iii)
M x=− ( mc ) r ω2
∑
i=1
N
sin ( ωt+αi )∗li
¿ ,− ( mc ) r ω2
∑
i=1
N
li∗sin (αi ) ………. (v)
Replacing with trigonometrical value of a1=a6 =0o , a2=a5 =120o , a3=a4=240o, l1=0, l2=a,l2=a
, l2=2 a, l2=3 a, l2=4 a, l2=5 a
∑
i=1
N
cos (ωt +α i )∗li=0∗cos ( 0o ) +a∗cos ( 120o ) +2 a∗cos ( 24 0o ) +3 a∗cos ( 240o ) +4 a∗cos ( 120o ) +5 a∗cos (0o)
¿ 0−0.5 a−a−1.5 a−2 a+5 a=0
In the same way, ∑
i=1
N
cos (2 αi )∗li is zero, and value for ∑
i=1
N
sin ( 2α i )∗li is zero.
Therefore, from equation (iv),
M z =0
8 | P a g e

Numerical on Balancing and Vibration
M x=0
From the above calculation of moment in x and z direction which is zero, we can say that, the
crank shaft with reciprocating piston is fully balanced
Solution -4
a)
Figure 1-Free Body diagram of mass m1 and m2
First of all we must determine equation of motion for given condition
The equation of motion for mass m1 can be given as
m1 ¨x1 +c1 ¿ …. (a)
Similarly, equation of motion for second mass
m2 ¨x2 +k2 x2−k2 x1 =0
−ω2 x1= ¨x1
9 | P a g e

Numerical on Balancing and Vibration
−ω2 m2 ¨x2 +k 2 x2−k2 x1=0
m2 ¨x2 + ˙x2 c2− ˙x1 c2+x2 k2−x1 k1=0………. (b)
The above equation in matrix form is
[m1 0
0 m2 ][ ¨x1
¨x2 ]+ [c1+ c2 −c2
−c1 c2 ][ ˙x1
˙x2 ]+ [k1 +k 2 −k2
−k 1 k2 ][x1
x2 ]=
[c1 ˙˙y + k1 y
0 ] Ans
Based on the above equation the frequency equation can be determined as follows
ω4− ( K1+ K2
m1 ) ω2 + k1 k2
m1 m2
=0 ………... (i)
The root of the above equation will, be required frequency
ω1
2 , ω2
2= k1 k2
2 m1
+ k2
2 m2
∓ √ 1
4 ( k1 k2
2 m1
+ k2
2 m2 )2
− k1 k 2
m1 m2
Ans
The mode vector, first we must harmonise the equation
r1= X2
( 1 )
X1
( 1 )
r2=−m1 ω1
2 +k1 + k2
k 2
………(c)
r2= X2
( 2 )
X1
( 2 ) ………(d)
r2=−m1 ω2
2 +k1 + k2
k 2
The phase angle of given system
ϕ1=tan−1
{ −r2 ˙x1 ( 0 ) + ˙x2 ( 0 )
ω1 [r 2 x1 ( 0 ) −x2 ( 0 ) ] }
ϕ2=tan−1
{ −r 1 ˙x1 ( 0 ) + ˙x2 ( 0 )
ω2 [r 1 x1 ( 0 ) +x2 ( 0 ) ] }
10 | P a g e

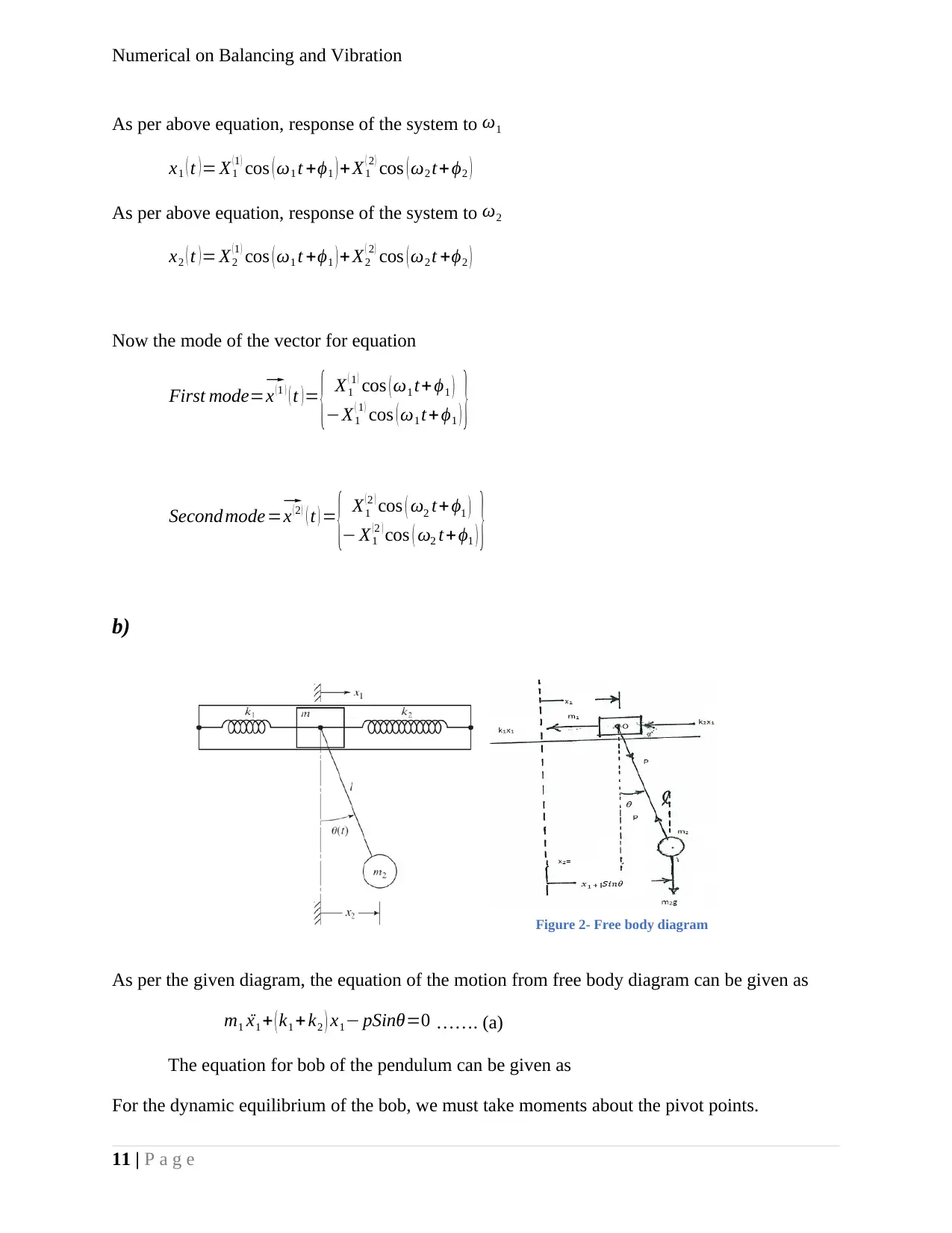
Figure 2- Free body diagram
Numerical on Balancing and Vibration
As per above equation, response of the system to ω1
x1 ( t ) = X1
( 1 ) cos ( ω1 t +ϕ1 ) +X1
( 2 ) cos ( ω2 t+ϕ2 )
As per above equation, response of the system to ω2
x2 ( t )= X2
(1 ) cos ( ω1 t +ϕ1 )+ X2
( 2 ) cos ( ω2 t +ϕ2 )
Now the mode of the vector for equation
First mode=⃗ x ( 1 ) ( t ) = { X1
( 1 ) cos ( ω1 t+ ϕ1 )
−X1
( 1 ) cos ( ω1 t+ ϕ1 ) }
Second mode=⃗ x ( 2 ) ( t ) = { X1
(2 ) cos ( ω2 t+ ϕ1 )
− X1
(2 ) cos ( ω2 t+ϕ1 ) }
b)
As per the given diagram, the equation of the motion from free body diagram can be given as
m1 ¨x1 + ( k1 +k2 ) x1− pSinθ=0 ……. (a)
The equation for bob of the pendulum can be given as
For the dynamic equilibrium of the bob, we must take moments about the pivot points.
11 | P a g e