Enzyme Reactions, Kinetics, and Inhibition: A Detailed Analysis

This assignment provides a detailed analysis of enzyme reactions and kinetics, beginning with the assumptions of the Michaelis-Menten model, including the steady-state condition and the derivation of the Michaelis constant (Km). It includes calculations of Ks and Km, followed by a practical analysis using provided data to estimate Vmax and Km through graphical methods. The document further explores reversible reactions and the significance of the equilibrium constant (Keq). It examines the effects of varying substrate concentrations on reaction rates and delves into enzyme inhibition, differentiating between competitive, non-competitive, and uncompetitive inhibition, complete with relevant equations and calculations. The document concludes with a calculation of reaction velocity using given parameters.

Running head: ENZYME REACTIONS 1
Enzyme reactions
Name:
Institution:

ENZYME REACTIONS 2
Question 1
Assumptions of the model
No products reverts backs to initial substrate. This is only practically true when product
concentration is very low
Since the ES may not be measurable, it should be expressed in measurable or known terms. This is
achieved by assuming steady state condition (Cornish-Bowden, 2014).
Rate of formation of ES=Rate of dissociation of ES
=K1 [E] [S]
Rate of breakdown of ES
=K3 [ES] =K3 [ES] +K2 [ES]
=K2 [ES]
(K3+K2)[ES]
At the steady state of ES
K1[S] [ES] = (k3+K2) [ES]
[ES]=K1[S] [E]/ (K2+K3)
Or ES=[S] [E]/ (K2+K3/K1)
Because the denominator is a constant expression can be reduced to [ES] =[S] [E]/Km
KM= (K2+K3/K1) where KM=michaeli’s constant
[E] is not measurable and must be expressed in a measurable terms

ENZYME REACTIONS 3
[E]free= [E] total-[ES]
Substituting the above equation
[ES]= ([E]total-[ES]) [S]/KM
[ES]=ET[S]/[S] +KM
Substituting the value of [ES] into the equation
V=K3ET[S]/[S] +KM
Vmax is attained when the enzyme is saturated with the substrate when [ET] = [ES]
Then Vmax=K3 [ET]
Substituting the equation
V=Vmax[S]/[S] +KM Michaeli’s Menten equation
Ks=K-1/k1
= (1*10^2)/ (1*10^7)
=1*10^-5M
Km=k-1+k2/k1
Km= (1*10^2+3*10^2)/ (1*10^7)
Km=4*10^-5M
Question 2a

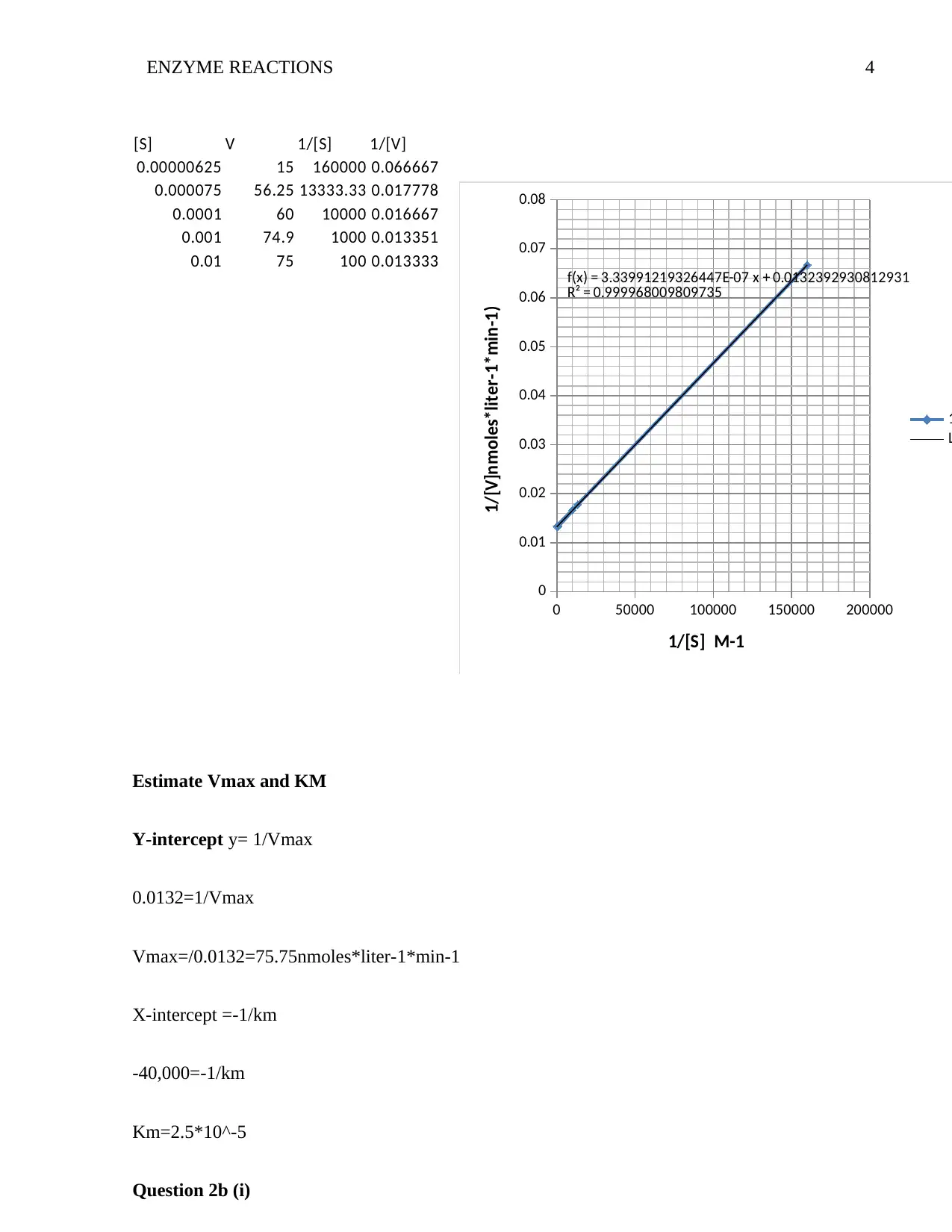
ENZYME REACTIONS 4
[S] V 1/[S] 1/[V]
0.00000625 15 160000 0.066667
0.000075 56.25 13333.33 0.017778
0.0001 60 10000 0.016667
0.001 74.9 1000 0.013351
0.01 75 100 0.013333
0 50000 100000 150000 200000
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
f(x) = 3.33991219326447E-07 x + 0.0132392930812931
R² = 0.999968009809735
1
L
1/[S] M-1
1/[V]nmoles*liter-1*min-1)
Estimate Vmax and KM
Y-intercept y= 1/Vmax
0.0132=1/Vmax
Vmax=/0.0132=75.75nmoles*liter-1*min-1
X-intercept =-1/km
-40,000=-1/km
Km=2.5*10^-5
Question 2b (i)

ENZYME REACTIONS 5
VO at [S] =2.5*10^-5
1/[S] =40,000
1/V=0.0256
V=38.46nmoles*liter-1*min-1
Question 2b (ii)
VO at [S] =5.0*10^-5
1[S] =20,000
1/ [V] at 20,000 equal to 50nmoles*liter-1*min-1
Question 2c
The substrate concentration would be the same
Question 3
S ⇋P the reversible reaction can progress in forward and backward direction. All reaction inclines
toward a state of chemical equilibrium, the state at which the forward action and reverse process
are taking place at similar rate (Engel, 2013). The equilibrium constant assists to comprehend
whether the reaction incline to have a greater concentration of reactant or products at equilibrium.
The magnitude of Keq can offer some insight about the product and reactant concentration at
equilibrium. If the Keq is very small, ~0.001 or less, then most reactant are present at equilibrium.
If Keq is very large, ~1000 or more, most product species will be existent at equilibrium. If Keq is
between 0.001 and 1000, will have significant concentration of reactant and product species
present at equilibrium (Engel, 2013).

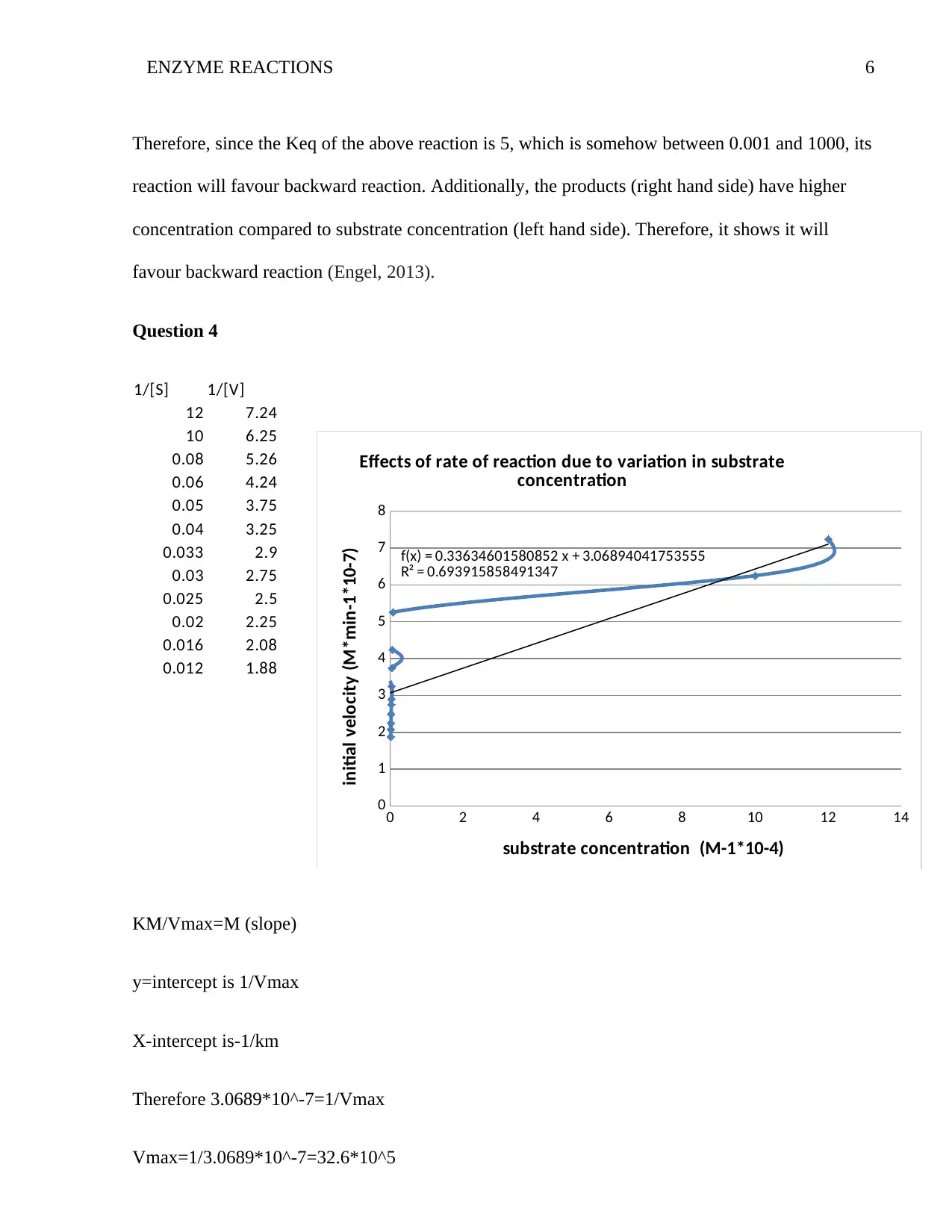
ENZYME REACTIONS 6
Therefore, since the Keq of the above reaction is 5, which is somehow between 0.001 and 1000, its
reaction will favour backward reaction. Additionally, the products (right hand side) have higher
concentration compared to substrate concentration (left hand side). Therefore, it shows it will
favour backward reaction (Engel, 2013).
Question 4
1/[S] 1/[V]
12 7.24
10 6.25
0.08 5.26
0.06 4.24
0.05 3.75
0.04 3.25
0.033 2.9
0.03 2.75
0.025 2.5
0.02 2.25
0.016 2.08
0.012 1.88
0 2 4 6 8 10 12 14
0
1
2
3
4
5
6
7
8
f(x) = 0.33634601580852 x + 3.06894041753555
R² = 0.693915858491347
Effects of rate of reaction due to variation in substrate
concentration
substrate concentration (M-1*10-4)
initial velocity (M*min-1*10-7)
KM/Vmax=M (slope)
y=intercept is 1/Vmax
X-intercept is-1/km
Therefore 3.0689*10^-7=1/Vmax
Vmax=1/3.0689*10^-7=32.6*10^5

ENZYME REACTIONS 7
X-intercept =-1/km
-10*10^3=-1/km
Km=-1/-10*10^3
Km=1.0*10^3
Question 5
5a, Competitive inhibition
Inhibitor binds to the active site, competing with substrate
I
S

I S
ENZYME REACTIONS 8
Equations:
E + S ES E + P Km ~ [E] [S]/ [ES]
E + I EI KI = [E] [I]/ [EI]
ET = [E] + [ES] +
[EI]
Derivation of modified Michaelis-Menten equation: V = Vmax[S]/ ([S] + Km
(1 + [I]/KI)) define Km, apparent = Km (1 +
[I]/KI) Note the effect of 1+ [I]/KI on Km:
As [I] increases, Km, apparent = Km (1 + [I]/KI) increases; at [I] = KI, Km, apparent = 2 x Km
(reduced “affinity” for S)
As [S] increases, [S] >> Km (1 + [I]/KI), and V --> Vmax
Line weaver-Burke formulation: again replace Km with Km (1 + [I]/KI)
1/V = {Km (1 + [I]/KI)/Vmax} (1/[S]) + 1/Vmax (Engel, 2013).
1/V= [4.7*10-5+ (1+ (5*10-4/3*10-4)22] [(1/ (2*10^-
4) + (1/22)]
1/V=[5.697*10^-6][5000.05]
V=35 nmoles*liter-1*min-1
5b, Non-competitive inhibition
Inhibitor and substrate bind to different sites

S I
ENZYME REACTIONS 9
Expect a lower Vmax, the same Km
E + S ES E + P
E + I EI
EI + S EIS
ES + I EIS
Km ~ [E] [S]/ [ES]; Ki = [E] [I]/ [EI] = [ES] [I]/ [ESI]
V = (Vmax/ (1 + [I]/Ki)) [S]
([S] + Km)
Vmax, apparent = Vmax/(1 + [I]/KI)
(1 + [I]/Ki)=2.667
(Vmax/ (1 + [I]/Ki) =8.25
22/ (1+5*10^-4]/ (3*10^-4) [2*10^-4=1.65*10^-3
(1.65*10^-3)/ [2*10^-4] [4.7*10^-5
V=6.68 nmoles*liter-1*min-1
5c, Uncompetitive inhibition
Inhibitor binds only to ES
E + S ES E + P
ES + I EIS
Expect a lower Vmax and a lower Km (!)
V = (Vmax/ (1 + [I]/Ki)) [S]
(Km/ (1 + [I]/Ki)) + [S]

ENZYME REACTIONS 10
Vmax, apparent = Vmax/ (1 + [I]/Ki); Km, apparent = Km/ (1 + [I]/Ki)
(1 + [I]/Ki)=2.667
= (Vmax/ (1 + [I]/Ki) =8.25
V = (Vmax/ (1 + [I]/Ki)) [S] =1.65*10^-3
(Km/ (1 + [I]/Ki)) + [S] =2.176*10^-4
V = (Vmax/ (1 + [I]/Ki)) [S]
(Km/ (1 + [I]/Ki)) + [S]
=7.582 nmoles*liter-1*min-1
Question 5d
1 / v = 1 / Vmax + Km / Vmax x 1 / [S]
Km / Vmax= (4.7*10^-5/22)=2.136
1 / [S] = (1/ (2*10^-4) =5,000
1 / Vmax=0.04545
Therefore=1/V=10,680
V=9.363*10^-5 nmoles*liter-1*min-1

ENZYME REACTIONS 11
References
Cornish-Bowden, A. (2014). Principles of enzyme kinetics. Elsevier, 1st ed, [Online]. Retrieved
from: https://books.google.com/books?
hl=en&lr=&id=Y62QBQAAQBAJ&oi=fnd&pg=PP1&dq=michaelis+menten+enzyme+k
inetics&ots=IZsUfadKfR&sig=gP-jm1kVHTSW7MlX4pEUuSwk3yI
Engel, P. C. (2013). Enzyme kinetics: the steady-state approach, 2nded, Springer. [Online].
Retrieved from: https://books.google.com/books?
hl=en&lr=&id=4PepBwAAQBAJ&oi=fnd&pg=PA7&dq=enzyme+kinetics&ots=qHTri
G7UZU&sig=XUYEb3Wp-0EctqG1tCws9M2YuDE