PSYC 105 Report: How Math Mastery Changes Equation Perception

This PSYC 105 report investigates whether mastering mathematics alters how individuals perceive mathematical equations. The study, conducted with 450 participants across three spacing conditions (consistent, inconsistent, and neutral), assessed their mathematical syntax knowledge and their accuracy in color judgment tasks related to mathematical expressions. The methodology involved comparing syntax knowers and non-knowers using two-sample t-tests to analyze the data. Results showed significant differences in performance between the two groups across all conditions, suggesting that mathematical expertise influences the perception of equations. The report includes descriptive statistics, hypothesis testing results, and a discussion of the findings, with strengths and limitations considered. The study concludes that mastering mathematics can indeed change how one sees mathematical equations.

Running head: PSYC 105 REPORT 1
Does Mastering Mathematics Change how you “see”
Mathematical Equations?
By
(Name of Student)
(Institutional Affiliation)
(Date of Submission)

PSYC 105 REPORT 2
Introduction
The mathematical practices are irrefutably perceptual. People look at geometric figures, does
inspection of these figure and read equations (Kirshner, 2019). In modern mathematical
encounter, a person is bound to scribble at the blackboard, draw diagrams, write equations and
step back to examine their inscription which must be seen to be used (Anderson, 2015). Now, the
question is, how can we make sense of all these perception within a mathematics task. Being a
competent mathematician would thus involve use of perception to read the equation and view the
diagrams and instantly translate the perceptual facts into much more intangible and internal
illustrations (Bliznakov & Adler, 2012).
This study aims at investigating whether people who are knowers and non-knowers of
mathematics impose perception and how mastering of mathematics can change how someone
sees a mathematical equation. The participants were examined for mastery of the basic
mathematical aspect in regard to change on how they perceive mathematical equations. The data
was collected and hypothesis testing performed. This report presents ad discusses the findings
from in relation to three main hypotheses identified.
Methodology
Participants
In this research, a total of 642 initial respondents were randomly selected for the study. The
participants were further allocated into 3 spacing conditions i.e. the consistent, inconsistent and
neutral. In order to uphold same number of respondents in these spacing conditions, we
identified and analyzed the data for the initial seventy five syntax knowers and non-knowers in
each and every condition. As a consequence of this, the final sample size obtained for this study

PSYC 105 REPORT 3
became 450 participants. In this case, 150 respondents in every spacing condition comprised of
seventy five respondents who knew the syntax and the other half comprised of those who were
syntax not knowers. Finally, the participation in this research was a voluntary basis and every
respondent was not obliged to participate.
Procedure
The participants were requested to perform some easy and simple mathematical calculations
such as addition, subtraction and multiplication. They were also asked to the level of
mathematics they took in their respective high schools. This was done so because we were
interested in evaluating how they perceive mathematical expression and how this could
influence their experiences (Anderson, 2015). A new measure of 25 mathematics questions were
used as a measure of mathematical syntax knowledge. This measure was developed based on the
two questions used in the Goldin-Meadow 2009 paper to evaluate mathematic syntax
knowledge in their research. Each correct response received a score of 1, with a maximum total
score of 25. This was converted to a percentage correct score. Participants with a score of 85
percent or higher (greater than 22 out of 25) were allocated into the ‘Syntax Knowers’ group
and participants with a score lower than percent ( less than 21 out of 25) were allocated into the
‘Syntax Non-Knowers’ group. Every equation with 4 reply options was presented in random
manner until the respondent responds or for 10 seconds whichever comes first. If participants
timed out (over 10 seconds) a ‘Too Slow” message was presented for 500ms (Goldstone, 2017)
Measures and Study design
The survey was designed not to take more than 30 minutes to complete and the responses were
completely anonymous implying that no identifying information was collected. The information

PSYC 105 REPORT 4
from all the participants will be utilized to compile the report and probable study publications by
the study group. In this study, the whole experiment was programmed and presented using the
Psy Toolkit software. Also, after granting the informed consent, the respondents were given a
chance to complete computer based task which comprised of a number of informations.
Ethical Consideration
In this study, the entire ethical aspect was taken care of by the approval of the research and its
activities by Macquarie University Human Research Ethics Committee. By this approval, all the
activities and factors entitled and linked with data collection via survey were well coordinated.
Analysis of Data
First, Signal detection theory was applied in analyzing the perceptual sensitivity while taking
control of important response bias (Marghetis, Landy & Goldstone, 2016). The remaining
analyses were performed in Stata version 14 software package where two sample tests were
performed in regard to the three hypotheses. All the assumptions were taken into consideration
and the level of significances kept the same through the analyses. The results are as given in the
next section below.
Results
Descriptive statistics
The descriptive statistics for age and sex was obtained as shown in the output below. The mean,
standard deviation, minimum, min were among the measure of dispersion obtained.
Table1: Descriptive Statistics

PSYC 105 REPORT 5
Hypothesis Testing
The findings of the three hypotheses tests are presented here. The hypotheses are all about
comparing the groups of syntax of not knowing and knowing respondents in each and every
spacing condition. Here, the measure of the participants’ accuracy for the colour judgment task
and knowledge was collected and analysed (Stoet, 2017). In each case, two sample t-test were
used in performing the tests and all the assumptions taken into consideration. The results are as
follows;
Hypothesis 1: Syntax Knowers vs. Non-Knowers (Neutral Spacing Condition)
Table 2: Two Sample t-test with Equal Variances

PSYC 105 REPORT 6
Hypothesis 2: Syntax Knowers vs. Non-Knowers (Consistent Spacing Condition)
Table 3: Two Sample t-test with Equal Variances
Hypothesis 3: Syntax Knowers vs. Non-Knowers (Inconsistent Spacing Condition)
Figure 4: Two Sample t-test with Equal Variances

PSYC 105 REPORT 7
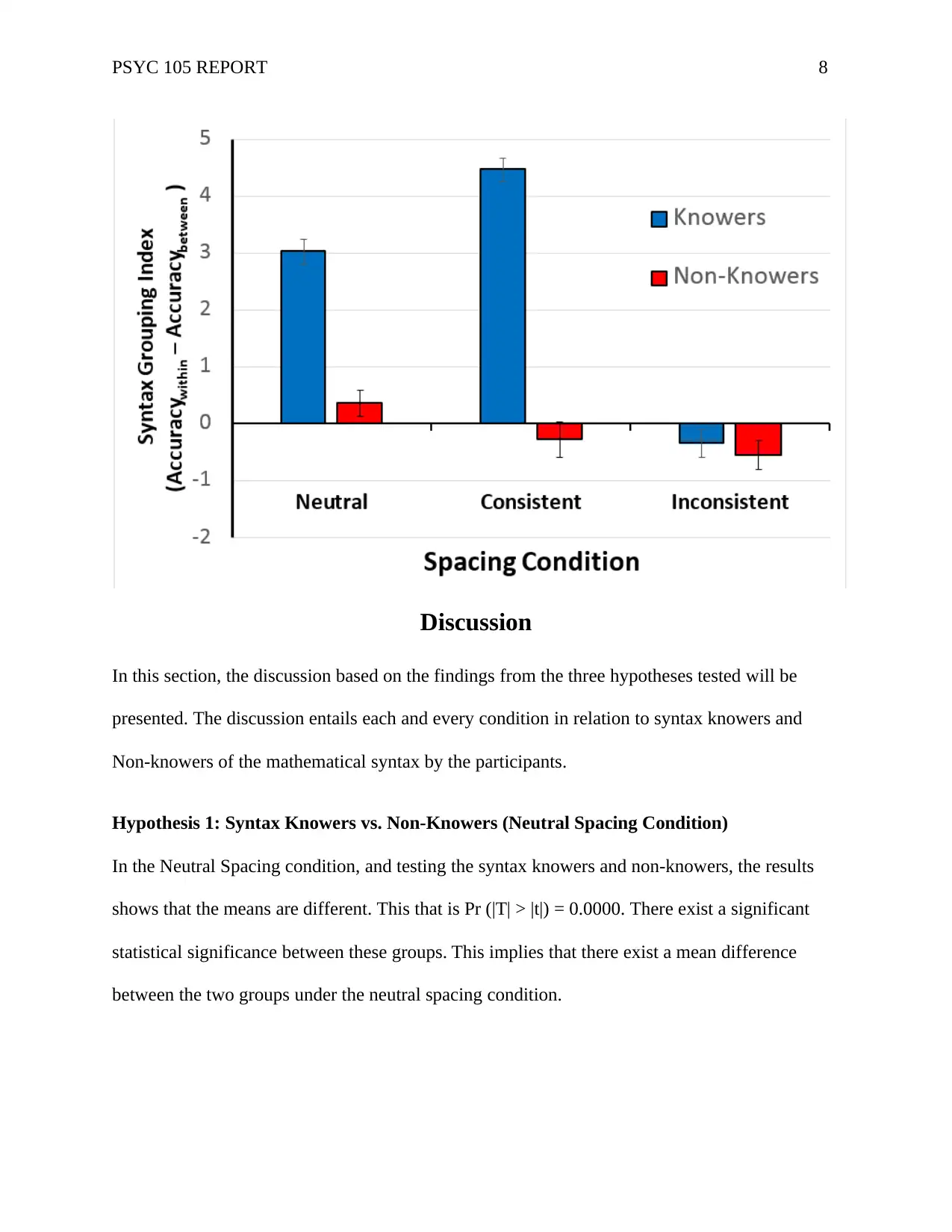
The box plots below shows the means of syntax grouping indexes alongside standard error bars
for the consistent, inconsistent and neutral conditions. The box plots also displays the syntax
knowers in blue bars and the non-knowers in red bars. As presented in the box plot, the syntax
grouping indexes is the dependent variable and thus gives a measure of the influence of learned
mathematics syntax grouping on the performance on the color identification activity. This was
calculated by subtracting the accuracy of the trials of color determination in which the color
tasks associate to the colored letters between the mathematics syntax grouping (i.e. s d l + p n
m), from the accuracy for trials in which the color tasks associate to the letters inside the
mathematics syntax grouping (i.e. s + d x l + n). That is to say Accuracy within minus Accuracy
between (Landy & Goldstone, 2007) This graph below illustrate the considerably higher syntax
grouping index for syntax knowers in blue bars as compared to not knowers in red bars for both
the consistent and neutral spacing conditions but not for the inconsistent spacing condition.
Figure 1: Box plots (Knowers and Non Knowers of Syntax)

PSYC 105 REPORT 8
Discussion
In this section, the discussion based on the findings from the three hypotheses tested will be
presented. The discussion entails each and every condition in relation to syntax knowers and
Non-knowers of the mathematical syntax by the participants.
Hypothesis 1: Syntax Knowers vs. Non-Knowers (Neutral Spacing Condition)
In the Neutral Spacing condition, and testing the syntax knowers and non-knowers, the results
shows that the means are different. This that is Pr (|T| > |t|) = 0.0000. There exist a significant
statistical significance between these groups. This implies that there exist a mean difference
between the two groups under the neutral spacing condition.

PSYC 105 REPORT 9
Hypothesis 2: Syntax Knowers vs. Non-Knowers (Consistent Spacing Condition)
Under this test with the same significant level, the results also suggest there exist a mean
difference between the two groups. That is Pr (|T| > |t|) = 0.0000. This also implies that under
consistent spacing condition, the syntax knowers and non-knowers have a different mastering as
far as mathematical syntax grouping on the performance on the color identification task is
concerned (Rivera & Garrigan, 2016).
Hypothesis 3: Syntax Knowers vs. Non-Knowers (Inconsistent Spacing Condition)
Finally on testing the mean difference between the syntax knowers and non-knowers under the
inconsistent condition, the results obtained as show in table 3 above suggest there still exist a
higher level within the groupings. That is Pr (|T| > |t|) = 0.5730. With this findings it can be
asserted that there exist a difference between the groups.
Strengths and limitations of the study
In this study, we only interviewed participants in regard to three selected conditions. This is a
major drawback since we are not well assured whether the participants were correctly grouped
into these categories. On the other hand, the analyses through hypothesis testing was well
performed on data and with this, better results were achieved.
Conclusion
Based on the results obtained from three hypotheses tested, it can be concluded that mastering
mathematics can change how one individual see mathematical equations. This is so due to the
fact that the results produced in all the three test were the same.

PSYC 105 REPORT 10
References
Anderson, J. R. (2015). Human symbol manipulation within an integrated cognitive
architecture. Cognitive science, 29(3), 313-341.
Bliznakov, E. G., & Adler, A. D. (2012). Nonlinear response of the reticuloendothelial system
upon stimulation. Pathobiology, 38(6), 393-410.
Goldin-Meadow, S., Cook, S. W., & Mitchell, Z. A. (2009). Gesturing gives children new ideas
about math. Psychological Science, 20(3), 267-272.
Goldstone, R. L., Marghetis, T., Weitnauer, E., Ottmar, E. R., & Landy, D. (2017). Adapting
perception, action, and technology for mathematical reasoning. Current Directions in
Psychological Science, 26(5), 434-441.
Kirshner, D. (2019). The visual syntax of algebra. Journal for Research in Mathematics
Education, 274-287.
Landy, D., & Goldstone, R. L. (2007). How abstract is symbolic thought? Journal of
Experimental Psychology: Learning, Memory, and Cognition, 33(4), 720.
Marghetis, T., Landy, D., & Goldstone, R. L. (2016). Mastering algebra retrains the visual
system to perceive hierarchical structure in equations. Cognitive research: principles and
implications, 1(1), 25.
Rivera, J., & Garrigan, P. (2016). Persistent perceptual grouping effects in the evaluation of
simple arithmetic expressions. Memory & cognition, 44(5), 750-761.
Stoet, G. (2010). PsyToolkit - A software package for programming psychological experiments
using Linux. Behavior Research Methods, 42(4), 1096-1104.

PSYC 105 REPORT 11
Stoet, G. (2017). PsyToolkit: A novel web-based method for running online questionnaires and
reaction-time experiments. Teaching of Psychology, 44(1), 24-31.