MAT540 Case Study: Linear Programming for Optimizing ER Staffing

This case study addresses the problem of optimizing emergency room nurse staffing to minimize costs while meeting demand. The emergency room operates 24/7, and the hospital seeks to manage nurse shift timings efficiently. The problem is formulated as a minimization problem using linear programming, with the objective function aiming to minimize the total salary paid to nurses. Constraints are based on the number of cases requiring attention during different time slots. The model considers nurses starting shifts at various times, with different productivity levels and pay rates. The solution, obtained using Excel Solver, indicates the optimal number of nurses to schedule at specific start times to meet demand while minimizing salary expenses. The case study demonstrates the practical application of linear programming in healthcare management.

MAT540 Assignment
Linear programming Case Study
Name of the Student
Name of the University
Author Note

Table of Contents
Background of the problem:..................................................................................................................3
Case details:...........................................................................................................................................3
LP Problem Formulation:.......................................................................................................................3
Excel solver output:...............................................................................................................................4
Conclusion:............................................................................................................................................5
Bibliography...........................................................................................................................................6

Background of the problem:
It has seen that emergency room in any hospital plays crucial role in hospital
operation. Depending on the demand, the emergency room operates 24*7 and
hence nurses who are doing shifts in emergency room works in different shifts. Now,
due to odd time factor, the hospital has to pay additional monetary benefits. Under
such circumstances, the management of the hospital needs to manage the shift
timing of individual nurses so that individual nurse can fulfill their usual shift timing
with minimum salary. Thus, this will be a minimization problem.
Case details:
The emergency room operates for 24 hours and have the following number of cases
during the indicated time slots:
Times 08-12 12-16 16-20 20-24 24-04 04-08
Cases/hr 3 12 8 11 4 3
There are three shifts starting at 8:00, 16:00 and 24:00. All nurses that start at these
times can handle 3 cases per hour and work 8 consecutive hours. Some nurses ask to
start at 12:00 or 20:00 and claim that they can work more productively handling 4
cases per hour if they let to start at 12:00 or 20:00 and work 8consecutive hours. The
emergency room pays equal salary to all nurses except for those working 24:00-
08:00shift, who earn 25% more. Salary for normal shift hours is $45
LP Problem Formulation:
Let x1, x2, x3, x4 and x5 will be the number of nurses starting at 08:00, 12:00, 16:00,
20:00 and 24:00 hours respectively. There will be no nurse who can start their shift at
04:00.
Hence, the objective function is:
Min Z = 45x1 + 45x2 + 45x3 + 45x4 + 56.25x5
The constraints are as follows:
3x1 >= 3
3x1 + 4x2 >= 12
4x2 + 3x3 >= 8
3x3 + 4x4 >= 11
4x4 + 3x5 >= 4
3x5 >= 3

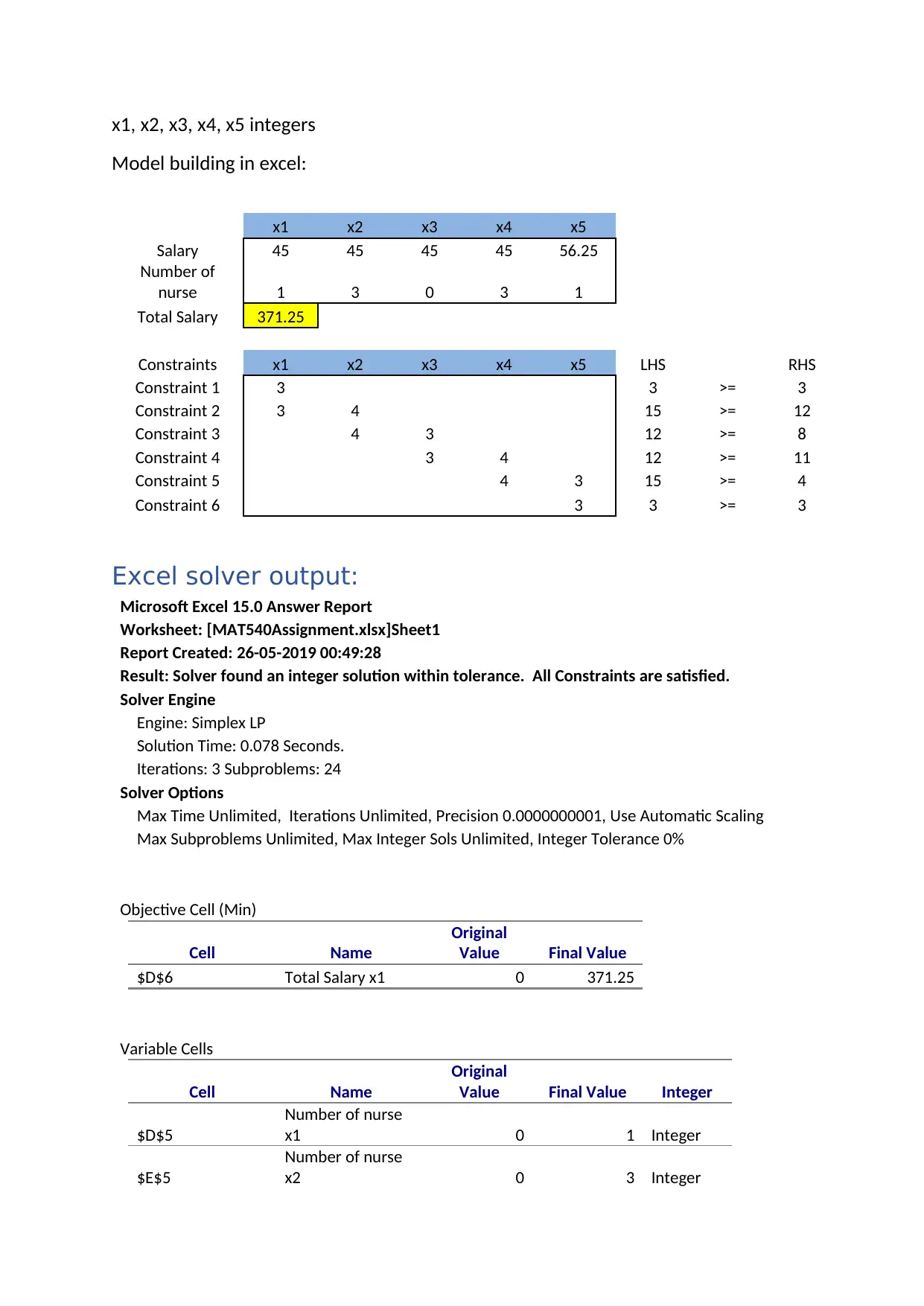
x1, x2, x3, x4, x5 integers
Model building in excel:
x1 x2 x3 x4 x5
Salary 45 45 45 45 56.25
Number of
nurse 1 3 0 3 1
Total Salary 371.25
Constraints x1 x2 x3 x4 x5 LHS RHS
Constraint 1 3 3 >= 3
Constraint 2 3 4 15 >= 12
Constraint 3 4 3 12 >= 8
Constraint 4 3 4 12 >= 11
Constraint 5 4 3 15 >= 4
Constraint 6 3 3 >= 3
Excel solver output:
Microsoft Excel 15.0 Answer Report
Worksheet: [MAT540Assignment.xlsx]Sheet1
Report Created: 26-05-2019 00:49:28
Result: Solver found an integer solution within tolerance. All Constraints are satisfied.
Solver Engine
Engine: Simplex LP
Solution Time: 0.078 Seconds.
Iterations: 3 Subproblems: 24
Solver Options
Max Time Unlimited, Iterations Unlimited, Precision 0.0000000001, Use Automatic Scaling
Max Subproblems Unlimited, Max Integer Sols Unlimited, Integer Tolerance 0%
Objective Cell (Min)
Cell Name
Original
Value Final Value
$D$6 Total Salary x1 0 371.25
Variable Cells
Cell Name
Original
Value Final Value Integer
$D$5
Number of nurse
x1 0 1 Integer
$E$5
Number of nurse
x2 0 3 Integer

$F$5
Number of nurse
x3 0 0 Integer
$G$5
Number of nurse
x4 0 3 Integer
$H$5
Number of nurse
x5 0 1 Integer
Constraints
Cell Name Cell Value Formula Status
Slac
k
$I$9 Constraint 1 LHS 3 $I$9>=$K$9 Binding 0
$I$10 Constraint 2 LHS 15
$I$10>=$K$1
0
Not
Binding 3
$I$11 Constraint 3 LHS 12
$I$11>=$K$1
1
Not
Binding 4
$I$12 Constraint 4 LHS 12
$I$12>=$K$1
2
Not
Binding 1
$I$13 Constraint 5 LHS 15
$I$13>=$K$1
3
Not
Binding 11
$I$14 Constraint 6 LHS 3
$I$14>=$K$1
4 Binding 0
$D$5:$H$5=Intege
r
Conclusion:
The above model has solved the problem and it is indicating that in order to meet
the demand, the hospital needs to schedule 1 nurse at 08:00 hours, 3 nurses at 12:00
hours, 3 nurses at 20:00 hours, and 1 nurse at 24:00 hours. The solution has also
shown that there is no need of starting any shift at 16:00 hours, which will minimize
the total salary.

Bibliography
Feijoo, G., Sanmartin, S. and Moreira, M.T., 2017. Implementation of linear
programming and life cycle approach in an Excel application to determine
ecoefficiency. In Computer Aided Chemical Engineering (Vol. 40, pp. 2731-2736).
Elsevier.
Wisniewski, M. and Klein, J.H., 2017. Critical Path Analysis and Linear Programming.
Macmillan International Higher Education.
Woubante, G.W., Alemu, A.B. and Gebrehiwot, S.A., 2019. Ensure optimum profit
using linear programming a product-mix of textile manufacturing companies.
International Journal of Mathematics in Operational Research, 14(3), pp.389-406.