Faculty of Science, MST125 TMA 01: Essential Mathematics 2 Solutions

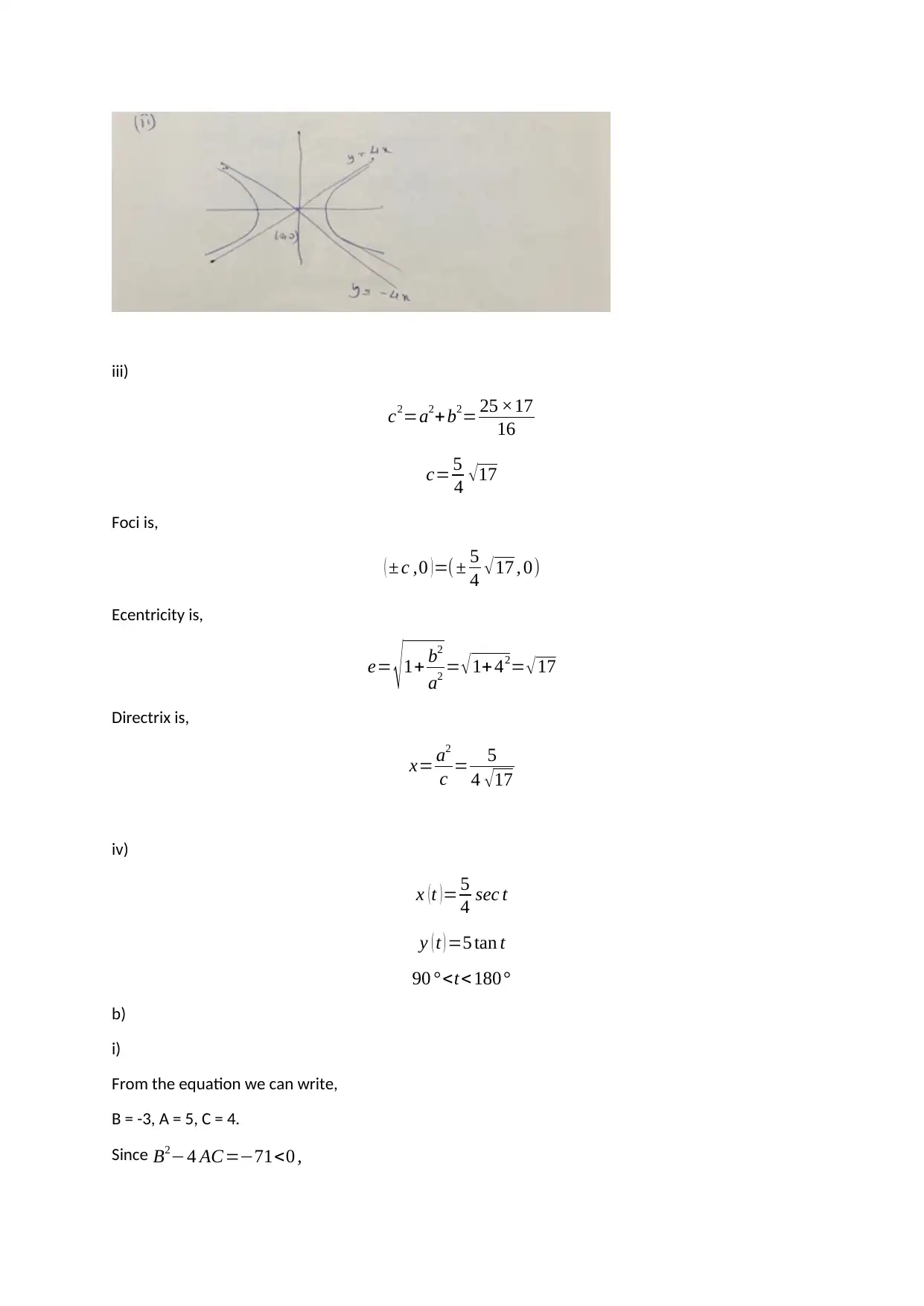
This document presents a detailed solution to the MST125 TMA 01 assignment for the Essential Mathematics 2 course, covering units 2, 3, 4, and 5. The solution includes step-by-step workings for each question, addressing topics such as distance and gradient calculations, modular arithmetic, solving linear congruences, conic sections (hyperbolas and ellipses), and vector mechanics. The assignment also delves into algebraic manipulations, finding equations of lines and curves, and applying trigonometric principles to solve force problems, including friction and tension calculations. The solutions provide insights into problem-solving techniques and mathematical reasoning, making it a valuable resource for students studying essential mathematics.

Question 1
MST125 TMA 01 Question 1
Microsoft word
1. The distance between A(x1 , y1 ) and B(x2 , y2 ) is given by,
AB= √ ( x2−x1 )
2+ ( y2− y1 ) 2
2. Hence the distance between A(−1, 3) and B ( 3,1 ) is
AB= √ ( 3−(−1) ) 2+ ( 1−3 ) 2
¿ √ 42+ 22
¿ √ 20
3. The gradient M of the line through ( x1 , y1 ) and ( x2 , y2 ) is given by,
m= y2− y1
x2−x1
Hence the distance between (−1,3) and ( 3,1 ) is
m= 1−3
3− (−1 ) =−2
4 =−1
2
The gradient of the line is −1
2 . Hence tan α=−1
2 . Let φ be the acute angle that the line
makes with the negative direction of the x axis. Then,
tan φ= 1
2
So,
φ=tan−1 1
2 =0.463
Hence,
α=π−0.463=2.677
Therefore the angle α is 2.68 radians (to 2 d.p.)
Question 2
a)
254 254 254 254 254
Sum of all the digits is = 11 + 11 + 11 + 11 + 11 = 55

Since 55 is not divisible by 9. So 254 254 254 254 254 is also not divisible by 9
b)
1356 modulo 19
1318 ≡ 1(mod 19)
1356=132 1354=169 (13¿¿ 18)3=169 ≡17(mod 19) ¿
Question 3
a)i)
27 v ≡1( mod 70)
27 v=1−70 w
27 v+70 w=1
70=2× 27+16
27=1× 16+11
16=1× 11+ 5
11=2 ×5+1
1=11−(2 ×5)
1=11− ( 2× ( 16−1×11 ) ) =3 ×11−2×16
1=3 × ( 27−1 ×16 ) −2 ×16=3× 27−5× 16
1=3 × 27−5 × (70−2 ×27 )=13 ×27−5 ×70
V = 13,
W = -5
27 ×13 ≡1 (mod 70)
27 x ≡ 10(mod 70)
13 ×27 x ≡ 13 ×10(mod 70)
x ≡ 13 0(mod 70)≡ 6 0(mod 70)
ii)
21 x=6+70 k
21 x−70 k=6

7 ( 3 x−10 k ) =6
Since ( 3 x−10 k ) is an integer and the equation won’t hold therefore we can say that no solution
exists
iii)
7 x ≡ 2(mod 10)
10=1×7 +3
7=2× 3+1
1=7−(2× 3)
1=7− ( 2 × ( 10−1× 7 ) ) =3× 7−2×10
V = 3,
W = -2
7 x ≡ 2(mod 10)
3 ×7 x ≡ 6( mod 10)
x ≡ 6( mod10)
b)
The answer is not coming.
Question 4
a)
i)
16 x2− y2=25
16 x2
25 − y2
25 =1
b=5∧a= 5
4
Vertex is (0, 0)
y=± b
a x =± 4 x
ii)

iii)
c2=a2+b2= 25 ×17
16
c= 5
4 √17
Foci is,
( ± c ,0 ) =(± 5
4 √ 17 , 0)
Ecentricity is,
e= √1+ b2
a2 = √1+ 42= √17
Directrix is,
x= a2
c = 5
4 √17
iv)
x (t )= 5
4 sec t
y ( t ) =5 tan t
90 °<t<180°
b)
i)
From the equation we can write,
B = -3, A = 5, C = 4.
Since B2−4 AC=−71<0 ,

We can say that it is a equation of the ellipse
ii)
Do not have the software to do the plot
Question 5
a)
x=3 t−4
y=t−4=¿ t= y +4
Putting t in x,
x=3 ( y +4 ) −4=3 y +8
y= 1
3 x −8
3
b)
d2= ( 3 t−5−4 t−2 ) 2+ ( t−4+ 2t−7 ) 2
d2= (−t−7 ) 2 + ( 3 t−11 ) 2
d2=t2 +49+14 t+9 t2 +121−66 t2=10 t2 −52t +170
c)
The mistakes are there in the last line and the second last line
d2=10 t2−52 t +170=10 ( t2−5.2t )+170
d2=10 ( t−2.6 ) 2−10 ( 6.76 ) +170=10 ( t−2.6 ) 2−67.6+170
d2=10 ( t −2.6 )2+102.4
The minimum occurs at t = 2.6 and the minimum value is
d2=102.4=¿ d =10.12
Question 6

F=μ N
N=(mg cos 15 °−T sin 20 °)
F=μ(mg cos 15 °−T sin 20°)
Force acting opposite to friction is given by,
( mg sin 15°−T cos 20 ° )=μ (mg cos 15° −T sin 20 °)
Solving for T we get,
T =81.205 Newton
Question 7
1)
F = 2N
So if we break in to the components
−i− √ 3 j
2)
F = 10 N
So if we break in to the components
−10 cos 20 °i−10 sin20 ° j=−9.397 i−3.42 j
G = 6 N
So if we break in to the components
6 cos 35 ° i+ 6 sin35 ° j=4.915 i+3.441 j
H is
−4.46i+0.02 j

Magnitude of H = 4.5 N and it makes 0 degree with horizontal towards left
3)
F = 85 N
So if we break in to the components
−85 cos 45 ° i+85 sin 45 ° j=−60.1i+60.1 j
G = G N
So if we break in to the components
−G i
H = H N
So if we break in to the components
H cos 30 °i−H sin 30 ° j=−60.1 i+60.1 j
Solving for the directions
We get,
H = 120.21 N
G = 44 N
4)
T1 is left and T2 is right
T 1 cos 45=T 2 cos 60
T 1=T 2
√2
In the vertical direction the force equation is,
T 1 sin 45+T 2sin 60=50 ×9.8
T 1
√ 2 + √3 T 2
2 =490
T 2
2 + √3 T 2
2 =490
T 2=358.7 N
T 1=253.64 N
5)
T is the tension
T sin 50=mg cos 35

T 1=T 2
√2
m=33.4 kg
6)
F=mg sin 20−¿ T cos 60=377.223 N ∈the opposite ¿ the assumed direction
7)
μ ¿
T =4937.34
8)
μ ¿
T =36.58=m1 g
m1=3.73