U22011 Structural Integrity: Fan Blade Damage Tolerance Analysis
VerifiedAdded on 2022/08/22
|14
|2384
|11
Report
AI Summary
This report presents a fracture mechanics analysis of an aero-engine fan blade, focusing on damage tolerance. The study begins with an introduction to the significance of fan blades in aero-engines and their susceptibility to fatigue failures, including high-cycle fatigue (HCF) and low-cycle fatigue (LCF). A comprehensive literature review explores common failure modes, fatigue analysis methods, and the application of crack growth analysis, particularly the Paris-Erdogan law. The methodology section details the mathematical analysis, using material properties of Ti-6Al-4V alloy, to determine the maximum stress acting at the crack and predict fatigue life. The analysis involves calculating bending and centrifugal stresses under various load conditions and applying the stress concentration factor. The results of the analysis demonstrate that the fatigue crack growth will be initiated due to the calculated stress falling in the cyclic stress range of operation. The discussion section highlights the importance of material selection, specifically the use of titanium-based alloys, and discusses the potential of metal matrix composite (MMC) and hybrid metallic materials as alternative options. The conclusion emphasizes the significance of damage tolerance analysis in ensuring flight safety and recommends more frequent inspections to detect crack growth. The report provides recommendations for enhancing the reliability and safety of aero-engine fan blades, supporting students with solutions on Desklib.

Running Head: DAMAGE TOLERANCE ANALYSIS
1
Part I: Fracture Mechanics Analysis of Engine Fan Blade
Student Name
Institutional Affiliation
1
Part I: Fracture Mechanics Analysis of Engine Fan Blade
Student Name
Institutional Affiliation
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

DAMAGE TOLERANCE ANALYSIS 2
Project I: FRACTURE MECHANICS ANALYSIS
INTRODUCTION
The fan components of an aero-engine have seen many design evolutions aimed at reducing the
weight and improving the aerodynamic performance of the plane. Aero-engine fan blades and
discs undergo subjection to high- and low-cyclic fatigue loads around contact points between
adjacent discs and blades. The low-cyclic fatigue (LCF) damage results from the centrifugal
forces that act on the fan blades while airfoil vibrations cause the high-cyclic fatigue (HCF)
damage. In structural integrity assessment, both the load components, that is, the centrifugal
forces and the airfoil vibrations must be considered in combination (Hou, Wicks & Antoniou,
2012).
This paper focusses on the fracture mechanics analysis of a solid fan blade of a small turbofan
aero-engine. The material of the targeted fan blades is the Ti-6Al-4V (Ti 6/4). The centrifugal
force experienced by the fan blade is assumed to be uniformly distributed tensile stresses across
the ends of the panel. The fan blade is assumed to be a center-cracked panel (Kozakiewicz et al.,
2016).
Project I: FRACTURE MECHANICS ANALYSIS
INTRODUCTION
The fan components of an aero-engine have seen many design evolutions aimed at reducing the
weight and improving the aerodynamic performance of the plane. Aero-engine fan blades and
discs undergo subjection to high- and low-cyclic fatigue loads around contact points between
adjacent discs and blades. The low-cyclic fatigue (LCF) damage results from the centrifugal
forces that act on the fan blades while airfoil vibrations cause the high-cyclic fatigue (HCF)
damage. In structural integrity assessment, both the load components, that is, the centrifugal
forces and the airfoil vibrations must be considered in combination (Hou, Wicks & Antoniou,
2012).
This paper focusses on the fracture mechanics analysis of a solid fan blade of a small turbofan
aero-engine. The material of the targeted fan blades is the Ti-6Al-4V (Ti 6/4). The centrifugal
force experienced by the fan blade is assumed to be uniformly distributed tensile stresses across
the ends of the panel. The fan blade is assumed to be a center-cracked panel (Kozakiewicz et al.,
2016).

DAMAGE TOLERANCE ANALYSIS 3
LITERATURE REVIEW
The service life of components of an aircraft is determined by the modes of fatigue and
degradation, such as fracture, fatigue, creep, yielding, wear, erosion, corrosion, etc. Fan blades
are crucial components of aero-engine and must be able to endure substantial thermal and
mechanical loading. When a problem arises with the fan blades, the whole aero-engines
performance is significantly affected and, consequently, the safety of the airplane. Broken fan
blades may be contained within the aero-engine casing and could cause puncture of the engine.
Failure and stress analysis of the fan blades of an aero-engine is thus a focus of numerous
research investigations (Amoo, 2013).
Common failures in aero-engine fan blades
The fan-blades may undergo mechanical damage, damage due to high-temperature exposure, and
creep failures. A more in-depth knowledge and understanding are gained on the damage
tolerance of these components through investigations of the crack initiation and propagation
mechanisms (Hou, Wicks & Antoniou, 2012).
High cyclic fatigue (HCF) failures often occur in the rotating parts of the aero-engines, such as
the fan blades. HCF failures result from fatigue loading, especially on materials with damages
sustained from other sources. The damage can be sustained from manufacturing defects or
developed during the service life of the aircraft. The low-cycle fatigue (LCF) has been identified
as the primary source of in-service damage that leads to HCF failures. Fretting and foreign object
damage (FOD) can also alter the HCF resistance in combination with LCF or individually (Zhao
& Zhang, 2010).
LITERATURE REVIEW
The service life of components of an aircraft is determined by the modes of fatigue and
degradation, such as fracture, fatigue, creep, yielding, wear, erosion, corrosion, etc. Fan blades
are crucial components of aero-engine and must be able to endure substantial thermal and
mechanical loading. When a problem arises with the fan blades, the whole aero-engines
performance is significantly affected and, consequently, the safety of the airplane. Broken fan
blades may be contained within the aero-engine casing and could cause puncture of the engine.
Failure and stress analysis of the fan blades of an aero-engine is thus a focus of numerous
research investigations (Amoo, 2013).
Common failures in aero-engine fan blades
The fan-blades may undergo mechanical damage, damage due to high-temperature exposure, and
creep failures. A more in-depth knowledge and understanding are gained on the damage
tolerance of these components through investigations of the crack initiation and propagation
mechanisms (Hou, Wicks & Antoniou, 2012).
High cyclic fatigue (HCF) failures often occur in the rotating parts of the aero-engines, such as
the fan blades. HCF failures result from fatigue loading, especially on materials with damages
sustained from other sources. The damage can be sustained from manufacturing defects or
developed during the service life of the aircraft. The low-cycle fatigue (LCF) has been identified
as the primary source of in-service damage that leads to HCF failures. Fretting and foreign object
damage (FOD) can also alter the HCF resistance in combination with LCF or individually (Zhao
& Zhang, 2010).
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

DAMAGE TOLERANCE ANALYSIS 4
Fatigue analysis of Aero-engine fan blades
The fan blades are attached to a disc that rotates as the shaft and the blades rotate. The blades are
thus subjected to both centrifugal forces and high vibrational and thermal stresses associated
with the high temperatures inside the engine (Farrokhabadi, Hosseini-Toudeshky &
Mohammadi, 2015).
The damage tolerance approach is often used to relate the remaining life of the engine
components, such as the fan blades based on the crack propagation rates. Vibratory stresses
from structural responses and unexpected drivers may exceed the capability of the material as
determined during sub-component tests of laboratory specimens. Gerber, Soderberg, and
Goodman's theories are some of the mean stress theories used to analyze fatigue failures. The
accidental introduction of damage to the material at the manufacturing level or during in-service
usage causes HCF failures due to fatigue loading on the materials. A threshold HCF resistance
below which no HCF failures will occur during the service operation is determined to account
for the high-frequency vibrational modes in the airfoil (Lin, 2014).
Fatigue analysis of Aero-engine fan blades
The fan blades are attached to a disc that rotates as the shaft and the blades rotate. The blades are
thus subjected to both centrifugal forces and high vibrational and thermal stresses associated
with the high temperatures inside the engine (Farrokhabadi, Hosseini-Toudeshky &
Mohammadi, 2015).
The damage tolerance approach is often used to relate the remaining life of the engine
components, such as the fan blades based on the crack propagation rates. Vibratory stresses
from structural responses and unexpected drivers may exceed the capability of the material as
determined during sub-component tests of laboratory specimens. Gerber, Soderberg, and
Goodman's theories are some of the mean stress theories used to analyze fatigue failures. The
accidental introduction of damage to the material at the manufacturing level or during in-service
usage causes HCF failures due to fatigue loading on the materials. A threshold HCF resistance
below which no HCF failures will occur during the service operation is determined to account
for the high-frequency vibrational modes in the airfoil (Lin, 2014).
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
DAMAGE TOLERANCE ANALYSIS 5
METHODS
Crack growth analysis
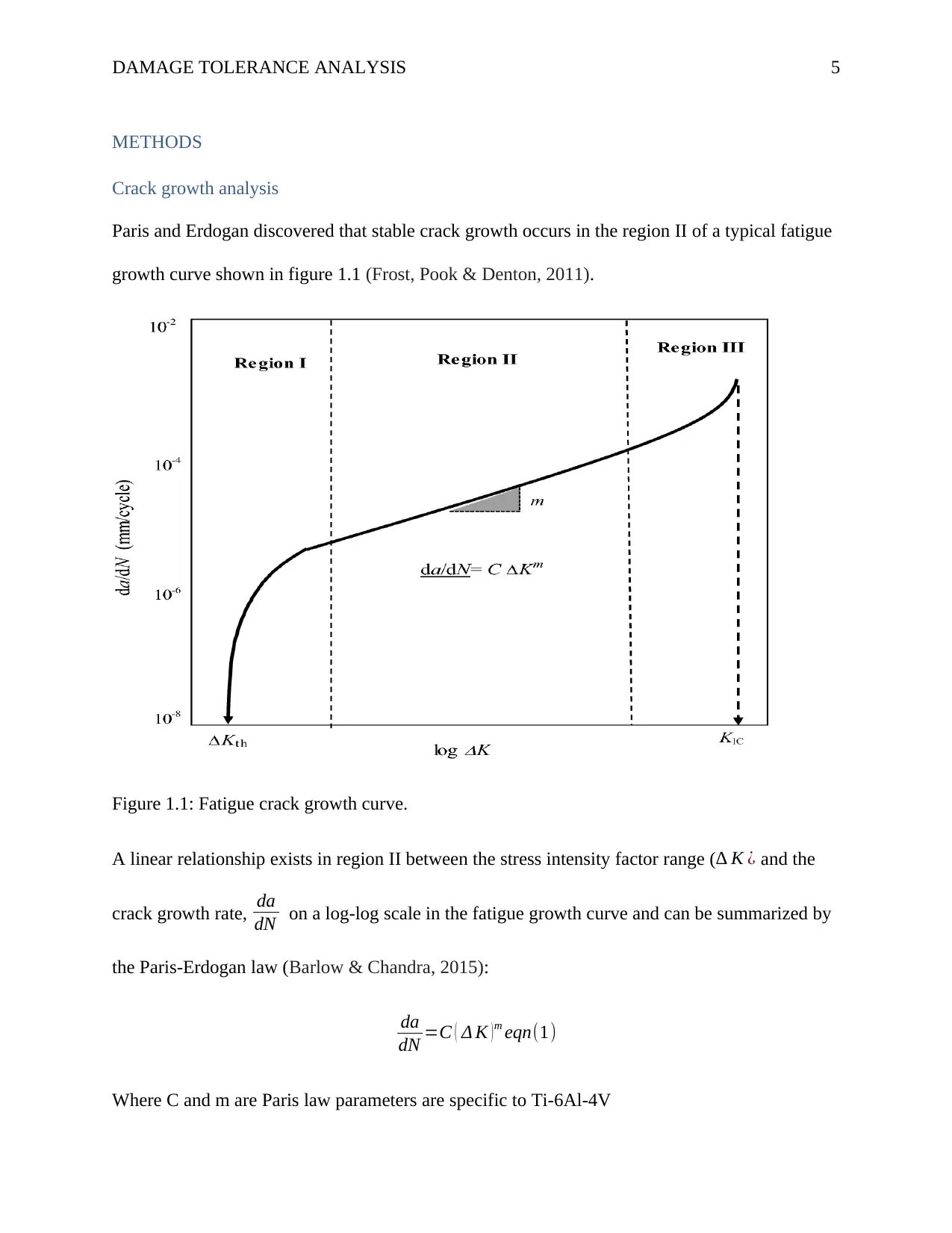
Paris and Erdogan discovered that stable crack growth occurs in the region II of a typical fatigue
growth curve shown in figure 1.1 (Frost, Pook & Denton, 2011).
Figure 1.1: Fatigue crack growth curve.
A linear relationship exists in region II between the stress intensity factor range ( ∆ K ¿ and the
crack growth rate, da
dN on a log-log scale in the fatigue growth curve and can be summarized by
the Paris-Erdogan law (Barlow & Chandra, 2015):
da
dN =C ( Δ K ) m eqn(1)
Where C and m are Paris law parameters are specific to Ti-6Al-4V
METHODS
Crack growth analysis
Paris and Erdogan discovered that stable crack growth occurs in the region II of a typical fatigue
growth curve shown in figure 1.1 (Frost, Pook & Denton, 2011).
Figure 1.1: Fatigue crack growth curve.
A linear relationship exists in region II between the stress intensity factor range ( ∆ K ¿ and the
crack growth rate, da
dN on a log-log scale in the fatigue growth curve and can be summarized by
the Paris-Erdogan law (Barlow & Chandra, 2015):
da
dN =C ( Δ K ) m eqn(1)
Where C and m are Paris law parameters are specific to Ti-6Al-4V

DAMAGE TOLERANCE ANALYSIS 6
The stress intensity factor range is determined from the maximum and the minimum values and
governs the fatigue crack growth in linear elastic fracture mechanics (LEFM) of the fan blades.
Δ K =Kmax −Kmin eqn (2)
For pure mode-I loading condition, ∆ K can be calculated using the ASTM standard formula
given by (Boiler & Code, 2017).
∆ K = ∆ P
B √ w
(2+ a
W )
(1− a
W )
3
2 [ 0.886+4.64 a
W −13.32 ( a
W )
2
+14.72 ( a
W )
3
−5.6 ( a
W ) 4
] eqn(3)
Where ∆ P is the range of stress force is, B is the thickness, and W is the width of the fan blade,
and a is the crack length.
The composition and material properties of the Ti-6Al-4V alloy used for the fan blades can be
summarized as in table 1.1, as obtained in the ASM material datasheet.
Composition/ Property Value
Titanium (Ti) 89.137 wt %
Aluminum (Al) 0.19 wt %
Nitrogen (N) 0.013 wt %
Oxygen (O) 0.19 wt %
Validium (V) 4.17 wt %
Fatigue strength 240 MPa
Stress concentration factor, Kt 3.3
The stress intensity factor range is determined from the maximum and the minimum values and
governs the fatigue crack growth in linear elastic fracture mechanics (LEFM) of the fan blades.
Δ K =Kmax −Kmin eqn (2)
For pure mode-I loading condition, ∆ K can be calculated using the ASTM standard formula
given by (Boiler & Code, 2017).
∆ K = ∆ P
B √ w
(2+ a
W )
(1− a
W )
3
2 [ 0.886+4.64 a
W −13.32 ( a
W )
2
+14.72 ( a
W )
3
−5.6 ( a
W ) 4
] eqn(3)
Where ∆ P is the range of stress force is, B is the thickness, and W is the width of the fan blade,
and a is the crack length.
The composition and material properties of the Ti-6Al-4V alloy used for the fan blades can be
summarized as in table 1.1, as obtained in the ASM material datasheet.
Composition/ Property Value
Titanium (Ti) 89.137 wt %
Aluminum (Al) 0.19 wt %
Nitrogen (N) 0.013 wt %
Oxygen (O) 0.19 wt %
Validium (V) 4.17 wt %
Fatigue strength 240 MPa
Stress concentration factor, Kt 3.3
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

DAMAGE TOLERANCE ANALYSIS 7
Modeling the fan blade as a rectangular plate of width, W equals 500mm and defect size, (2a)
given as 0.5mm, the bending stress in the fan blade is calculated as follows (Frost, Pook &
Denton, 2011).:
σ bending= M
W b
eqn(5)
Where M =P . e is the moment and W b = I
| y|max
with I the moment of inertia and |y|max the
maximum distance from a neutral point.
The pressure load, P and the cross-sectional area, of the fan blade, is used to calculate direct
stress (also known as the centrifugal stress) as:
σ direct = P
A eqn(6)
The maximum stress acting on the fan blade is given as the sum of the two stresses:
σ tot=σ direct ± σbending eqn(7)
From geometry of the fan blade,
A=W ×a=500 ×0.25=125 mm2
Wb = I
| y|max
= W 2 ×a
6 = 5002 ×0.25
6 =10,416.67
Assuming that a pressure load of P=1000 N is acting on the fan blade, the direct and the bending
stress can be calculated using equations (6) and (5) respectively (Lin, 2014):
σ direct = P
A =1000
125 =8 MPa
Modeling the fan blade as a rectangular plate of width, W equals 500mm and defect size, (2a)
given as 0.5mm, the bending stress in the fan blade is calculated as follows (Frost, Pook &
Denton, 2011).:
σ bending= M
W b
eqn(5)
Where M =P . e is the moment and W b = I
| y|max
with I the moment of inertia and |y|max the
maximum distance from a neutral point.
The pressure load, P and the cross-sectional area, of the fan blade, is used to calculate direct
stress (also known as the centrifugal stress) as:
σ direct = P
A eqn(6)
The maximum stress acting on the fan blade is given as the sum of the two stresses:
σ tot=σ direct ± σbending eqn(7)
From geometry of the fan blade,
A=W ×a=500 ×0.25=125 mm2
Wb = I
| y|max
= W 2 ×a
6 = 5002 ×0.25
6 =10,416.67
Assuming that a pressure load of P=1000 N is acting on the fan blade, the direct and the bending
stress can be calculated using equations (6) and (5) respectively (Lin, 2014):
σ direct = P
A =1000
125 =8 MPa
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
DAMAGE TOLERANCE ANALYSIS 8
σ bending= M
W b
= P. e
W b
= (1000 × 0.25 )
10,416.67 =0.024 MPa
Total stress is calculated from equation (7)
σ tot=8+0.024=8.024 MPa
High-stress concentrations exist near the center crack than the rest of the fan blade and the stress
concentration factor, Kt is used to calculate the maximum stress at the notch as (Frost, Pook &
Denton, 2011).:
σ max=K t σtot
σ max=3.3 × 8.024 MPa=26.48 MPa
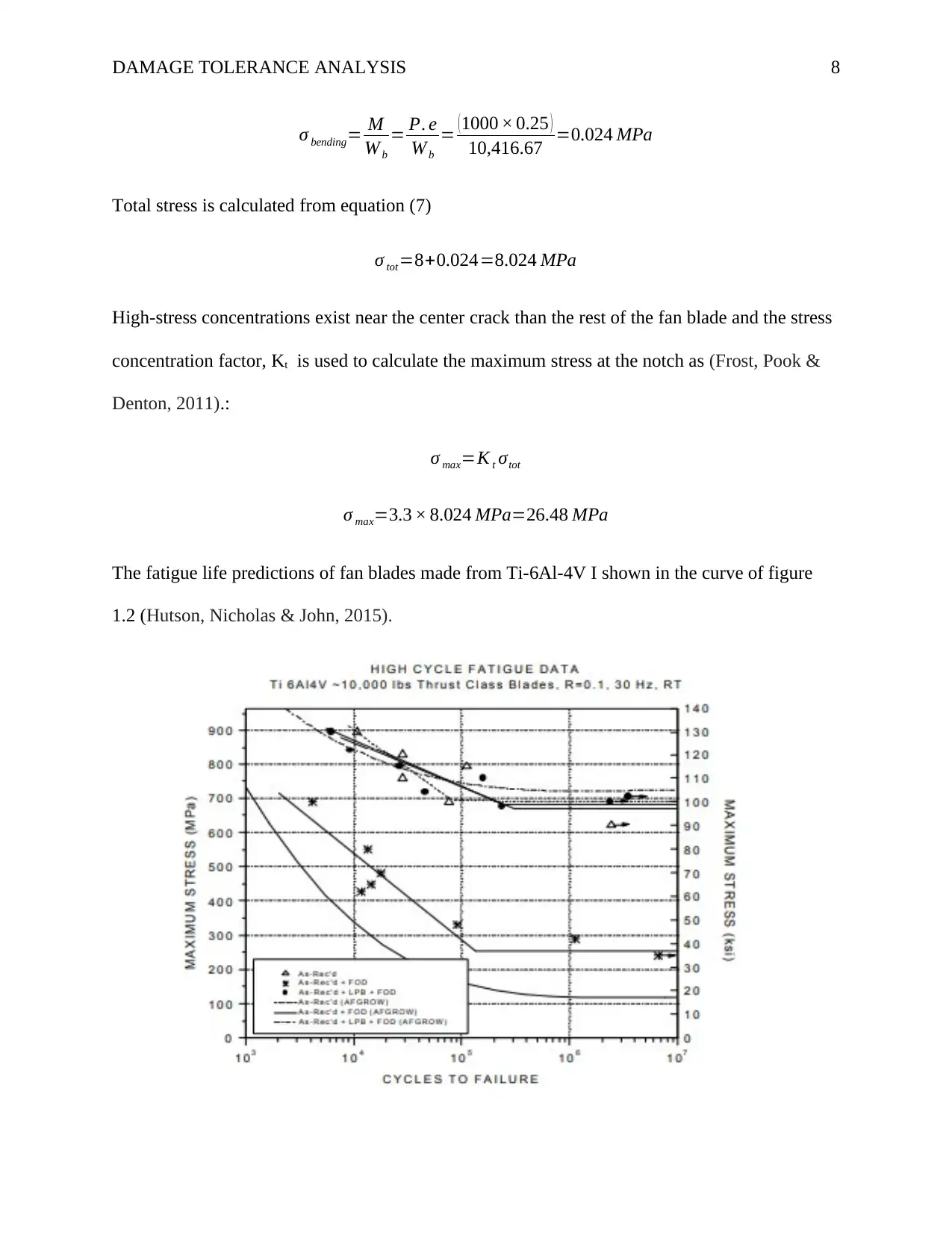
The fatigue life predictions of fan blades made from Ti-6Al-4V I shown in the curve of figure
1.2 (Hutson, Nicholas & John, 2015).
σ bending= M
W b
= P. e
W b
= (1000 × 0.25 )
10,416.67 =0.024 MPa
Total stress is calculated from equation (7)
σ tot=8+0.024=8.024 MPa
High-stress concentrations exist near the center crack than the rest of the fan blade and the stress
concentration factor, Kt is used to calculate the maximum stress at the notch as (Frost, Pook &
Denton, 2011).:
σ max=K t σtot
σ max=3.3 × 8.024 MPa=26.48 MPa
The fatigue life predictions of fan blades made from Ti-6Al-4V I shown in the curve of figure
1.2 (Hutson, Nicholas & John, 2015).

DAMAGE TOLERANCE ANALYSIS 9
Figure 1.2: Fatigue life predictions of fan blades
From figure 1.2, the fatigue life of the fan blades can be predicted for the base loading cycle of
0-220 MPa. At 220 MPa: t predict=2× 104=20,000hours. The 70% of the predicted life is given by
0.7 × 20,000=14000 hours. An inspection should be scheduled after 14000 hours.
ANALYSIS
Mathematical analysis was used to determine the maximum stress acting at the crack, taking into
consideration the stress concentration factor of Ti-6Al-4V. The calculated stress of 26.48 MPa
obtained at a pressure load of 1000 N falls in the cyclic stress range of operation, and
consequently, a fatigue crack growth will be initiated (Boiler & Code, 2017).
When the maximum stress is increased by 50 %, the new stress to which the fan blade is
subjected is obtained as:
σ max ( new ) =σmax ( old ) + 50
100 ×σ max ( old )
σ max ( new ) =26.48+ 50
100 ×26.48=39.72 MPa
The fatigue crack growth will occur at an increased rate due to increased maximum stress (
39.72 MPa¿ , which falls within the specified unchanged cyclic stress range. The fan blade is
assessed for strength when sustaining an overload of 5 times the nominal stress. The new
pressure load will be 5000 N and bending, and centrifugal stresses are re-calculated using
equations (6) and (5) respectively (Lin, 2014):
Figure 1.2: Fatigue life predictions of fan blades
From figure 1.2, the fatigue life of the fan blades can be predicted for the base loading cycle of
0-220 MPa. At 220 MPa: t predict=2× 104=20,000hours. The 70% of the predicted life is given by
0.7 × 20,000=14000 hours. An inspection should be scheduled after 14000 hours.
ANALYSIS
Mathematical analysis was used to determine the maximum stress acting at the crack, taking into
consideration the stress concentration factor of Ti-6Al-4V. The calculated stress of 26.48 MPa
obtained at a pressure load of 1000 N falls in the cyclic stress range of operation, and
consequently, a fatigue crack growth will be initiated (Boiler & Code, 2017).
When the maximum stress is increased by 50 %, the new stress to which the fan blade is
subjected is obtained as:
σ max ( new ) =σmax ( old ) + 50
100 ×σ max ( old )
σ max ( new ) =26.48+ 50
100 ×26.48=39.72 MPa
The fatigue crack growth will occur at an increased rate due to increased maximum stress (
39.72 MPa¿ , which falls within the specified unchanged cyclic stress range. The fan blade is
assessed for strength when sustaining an overload of 5 times the nominal stress. The new
pressure load will be 5000 N and bending, and centrifugal stresses are re-calculated using
equations (6) and (5) respectively (Lin, 2014):
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

DAMAGE TOLERANCE ANALYSIS 10
σ direct = P
A =5000
125 =40 MPa
σ bending= M
W b
= P. e
W b
= ( 5000 × 0.25 )
10,416.67 =0.12 MPa
σ tot=40+ 0.12 MPa=40.12 MPa
σ max=3.3 × 40.12=132.396 MPa
The fan blade will still be strong enough to sustain a 5-times overload at a pressure load of 1000
N.
Superimposition of the major stress cycle of the fan blade with a minor vibrational cycle of 200-
240 MPa leads to more frequent scheduled inspections due to the reduction of component life.
From figure 1.2, at 240 MPa, t predict=1.5× 104 =15 ,000 hours
New inspection period is 0.7 ×15 , 000=10500 hours
Small scale yielding (SSY) condition is met for all cases, and the material will eventually yield
under the calculated stress conditions (Boiler & Code, 2017).
σ direct = P
A =5000
125 =40 MPa
σ bending= M
W b
= P. e
W b
= ( 5000 × 0.25 )
10,416.67 =0.12 MPa
σ tot=40+ 0.12 MPa=40.12 MPa
σ max=3.3 × 40.12=132.396 MPa
The fan blade will still be strong enough to sustain a 5-times overload at a pressure load of 1000
N.
Superimposition of the major stress cycle of the fan blade with a minor vibrational cycle of 200-
240 MPa leads to more frequent scheduled inspections due to the reduction of component life.
From figure 1.2, at 240 MPa, t predict=1.5× 104 =15 ,000 hours
New inspection period is 0.7 ×15 , 000=10500 hours
Small scale yielding (SSY) condition is met for all cases, and the material will eventually yield
under the calculated stress conditions (Boiler & Code, 2017).
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

DAMAGE TOLERANCE ANALYSIS 11
DISCUSSION
The choice of fan blade materials is essential especially to their damage tolerance. The ductility,
yield strength, and high-cycle fatigue strength are other factors that are taken into consideration
during materials (Boller & Seeger, 2013). Unique physical, mechanical, and corrosion properties of
Titanium-based alloys such as Ti-6Al-4V have made them the obvious choice for good
aerodynamic performance. Moreover, Titanium is readily available and easy to fabricate. The
main drawback of using titanium is its very high cost that makes fan blade construction too
expensive (Poursaeidi & Salavatian, 2009).
Researchers have started looking at metal matrix composite (MMC) and hybrid metallic
materials as a cheaper options for fan blades construction. MMC materials are very light due to
the high strength-to-density and stiffness-to-density ratios that they offer, thus contributing to the
overall weight savings of the engine. Hybrid metallic materials have improved structural
strengths and provide both weight and structural benefits. The main disadvantages of MMC
materials are too expensive in the wide application of fan blade manufacturing. Hybrid metallic
materials are not durable (Boiler & Code, 2017).
More frequent damage tolerance analysis should be conducted if the MMC material and hybrid
metallic materials are used for fan blades. This is important in the determination of the remaining
life of the fan blades since these materials are not as durable as Titanium-based alloys (Zhao &
Zhang, 2010)..
DISCUSSION
The choice of fan blade materials is essential especially to their damage tolerance. The ductility,
yield strength, and high-cycle fatigue strength are other factors that are taken into consideration
during materials (Boller & Seeger, 2013). Unique physical, mechanical, and corrosion properties of
Titanium-based alloys such as Ti-6Al-4V have made them the obvious choice for good
aerodynamic performance. Moreover, Titanium is readily available and easy to fabricate. The
main drawback of using titanium is its very high cost that makes fan blade construction too
expensive (Poursaeidi & Salavatian, 2009).
Researchers have started looking at metal matrix composite (MMC) and hybrid metallic
materials as a cheaper options for fan blades construction. MMC materials are very light due to
the high strength-to-density and stiffness-to-density ratios that they offer, thus contributing to the
overall weight savings of the engine. Hybrid metallic materials have improved structural
strengths and provide both weight and structural benefits. The main disadvantages of MMC
materials are too expensive in the wide application of fan blade manufacturing. Hybrid metallic
materials are not durable (Boiler & Code, 2017).
More frequent damage tolerance analysis should be conducted if the MMC material and hybrid
metallic materials are used for fan blades. This is important in the determination of the remaining
life of the fan blades since these materials are not as durable as Titanium-based alloys (Zhao &
Zhang, 2010)..

DAMAGE TOLERANCE ANALYSIS 12
CONCLUSIONS
Assuming the fan blade to be a center-cracked panel, fracture mechanics analysis was conducted
to determine the toughness of the component and to assess the fatigue crack growth rate. Crack
growth curves were used at specific stress integrity factor to determine the fatigue stress. From
the crack growth rate, the period between technical inspections of the aero-engines were
determined. As a recommendation, more frequent damage tolerance analysis should be done to
detect the crack growth level before it reaches a critical size to avoid catastrophic rupture. Such
analyses would ensure flight security and safety.
CONCLUSIONS
Assuming the fan blade to be a center-cracked panel, fracture mechanics analysis was conducted
to determine the toughness of the component and to assess the fatigue crack growth rate. Crack
growth curves were used at specific stress integrity factor to determine the fatigue stress. From
the crack growth rate, the period between technical inspections of the aero-engines were
determined. As a recommendation, more frequent damage tolerance analysis should be done to
detect the crack growth level before it reaches a critical size to avoid catastrophic rupture. Such
analyses would ensure flight security and safety.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 14
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.
