Mathematics for Business and Finance: Solutions and Analysis
VerifiedAdded on 2022/08/21
|10
|458
|22
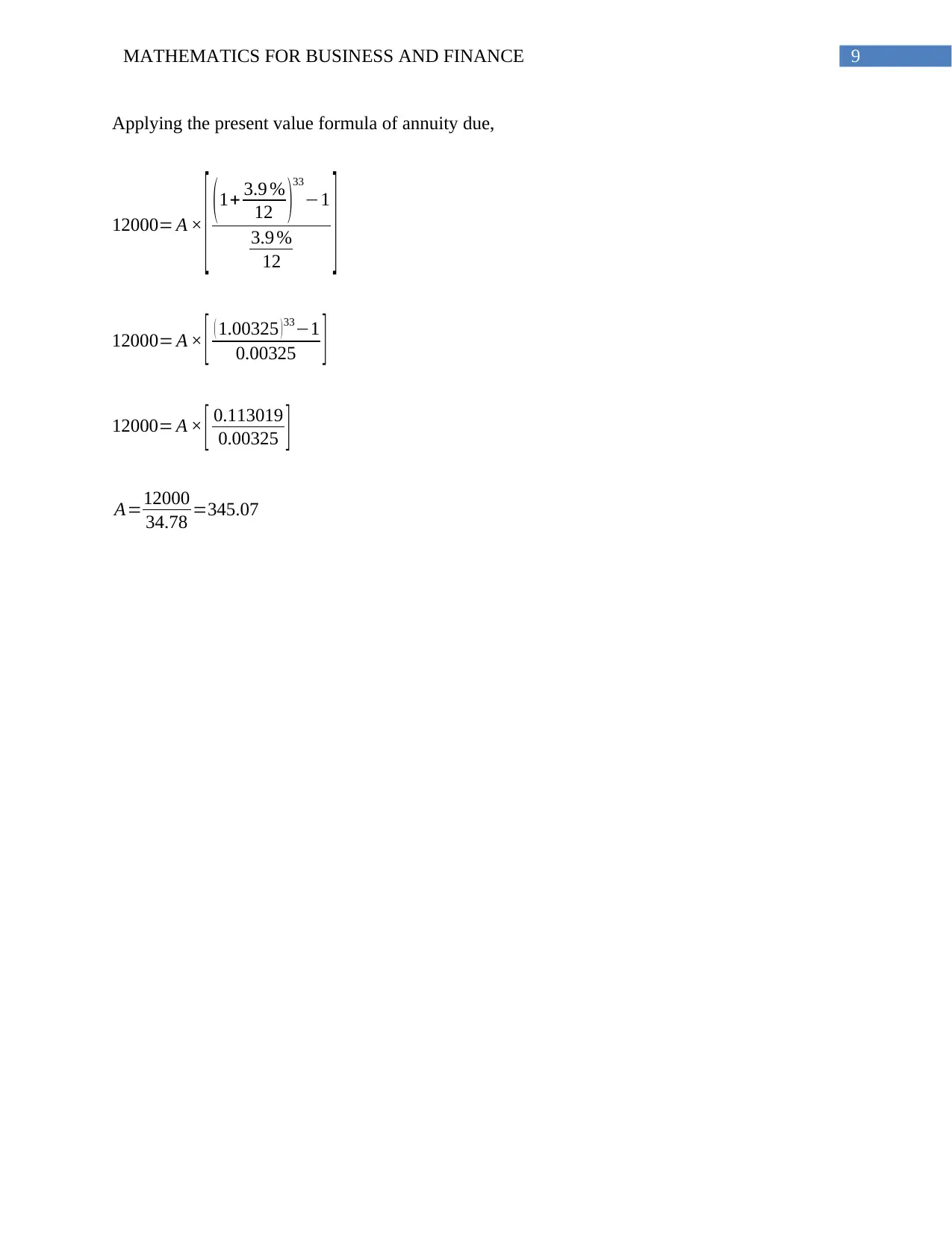
Homework Assignment
AI Summary
This document presents a comprehensive solution to a Mathematics for Business and Finance assignment. The assignment covers various financial calculations, including present and future value of money, compound interest, and annuities. The solutions demonstrate the application of formulas to solve problems related to periodic withdrawals, loan terms, and investment planning. The student addresses questions involving the calculation of present values, effective interest rates, and the number of periods required to reach specific financial goals. The document includes detailed steps, formulas, and explanations for each problem, providing a clear understanding of the financial concepts involved. The assignment covers topics such as calculating the term of a loan, determining the time required for an investment to grow to a certain amount, and analyzing the impact of different interest rates and compounding periods. Overall, the assignment provides a practical application of mathematical principles in a business and financial context.
1 out of 10
















![[object Object]](/_next/static/media/star-bottom.7253800d.svg)