Finance Assignment: Valuation of Shares, Capital Budgeting, and Loans

This finance assignment solution addresses several key concepts in financial analysis. The first question involves a two-period certainty model, calculating consumption and income based on dividend payouts and equity holdings. The second question focuses on share valuation, determining the current selling price of a share given dividend growth expectations. The third question covers time value of money, deferred annuities, and loan repayments, including calculations for retirement funds, monthly pensions, effective interest rates, and loan amortization. The final question delves into capital budgeting, evaluating two mutually exclusive projects using payback period, NPV, IRR, and crossover point analysis, along with a capital budgeting problem for a new technology purchase, considering costs, savings, depreciation, and tax implications to determine the net present value of the investment.

QUESTION `1. [6 + 6 = 12 Marks.]
a) This is a two period certainty model problem.
Assume that Jillian Black has a sole income from Halcyon Ltd in which she owns
10% of the ordinary share capital.
In its financial year 2016-17 just ended, Halcyon Ltd reported net profits after tax
of $800,000, and announced its net profits after tax expectation for the next
financial year, 2017-18, to be 20% higher than this year’s figure. The company
operates with a dividend payout ratio of 80%, which it plans to continue, and will
pay the annual dividend for 2016-17 in mid-January, 2018, and the dividend for
2017-18 in mid-January, 2019.
In mid-January, 2019, Jillian wishes to spend $100,000, which will include the
cost of new furniture. How much can she consume in mid-January, 2018 if the
capital market offers an interest rate of 8% per year?
Answer:
Income Estimations
Year 2016-17 2017-18
Net Profit 800000 960000
Dividend Payout 80% 80%
Dividend 640000 768000
Equity holding of Jillian Black 10% 10%
Dividend of Jillian Black 64000 76800
Two period Certainty problem
Year Income Opening Amount Interest Consumption Balance
2016-2017 64000 0 5760 69120 54176.88 14943.12
2017-2018 76800 14943.12 8256.88 100000 100000 0
1

b) This question relates to the valuation of shares.
Ram Shack Ltd has just paid a dividend of $3.00 a share. Investors require a
13% per annum return on investments such as Ram Shack. What would a share
in Ram Shack Ltd be expected to sell for today (January, 2018) if the dividend is
expected to increase by 20% in January, 2019, 16% in January, 2020, 12% in
January, 2021 and thereafter by 5 per cent a year forever, from January, 2022
onwards?
Answer:
Year Dividend PVF @ 13%
PV of
Dividend
2018 3.00 0.885 2.655
2019 3.60 0.783 2.819
2020 4.18 0.693 2.894
2021 4.68 0.613 2.869
2022 61.39* 0.543 33.319
Price of Share 44.555
* 4.68 x (1+0.05)/(0.13-0.05)= 61.39
2

QUESTION 2. [(4 + 4) + (2 + 3 + 3 + 3 + 3) = 22 Marks]
a) This question relates to the time value of money and deferred annuities.
Colin Way is age 40 today and plane to retire on his 65th birthday. With future
inflation, Colin estimates that he will require around $2,000,000 at age 65 to
ensure that he will have a comfortable life in retirement. He believes that he can
contribute $3,000 at the end of each month, starting in one months’ time and
finishing on his 65th birthday.
i) If the fund to which he contributes earns 6% per annum, compounded
monthly (after tax), how much will he have at age 65? Will he have
achieved his targeted sum? What is the surplus or the shortfall?
Answer:
Total fund Balance on his 65th Birthday 20,78,981.89
Required Amount 20,00,000.00
Surplus 78,981.89
Hence, the surplus amount is $78981.89.
(Refer Appendix)
ii) Using the fund balance, Colin then wishes to commence a monthly
pension payable by the fund starting one month after his 65th birthday,
and ending on his 85th birthday, after which he expects that the fund will
be fully expended. If the fund continues to earn the above return of 6%
per annum, compounded monthly, how much monthly pension will Colin
receive, if the fund balance reduces to zero as planned after the last
pension payment on his 85th birthday?
Answer:
The fund balance $ 78,981.89
The amount of monthly pension = $567.08
(Refer appendix)
b) This question relates to loan repayments and loan terms.
Ray and Betty Read wish to borrow $600,000 to buy a home. The loan from
Battlers Bank requires equal monthly repayments over 20 years, and carries.an
interest rate of 4.8% per annum, compounded monthly. The first repayment is
due at the end of the first month.
You are required to calculate:
i) The effective annual interest rate on the above loan.
Answer:
Nominal Interest rate 0.048
Monthly Interest Rate 0.004
Effective Interest Rate (1+r/n)^n
Effective Interest Rate 4.91%
ii) the amount of the monthly repayment (consisting of interest and principal
repayment components) if the same amount is to be repaid every month
over the 20 year period of the loan.
Answer:
3
Installment= Loan Amount/(1+r)^240
Loan 6,00,000.00
R 0.004
Installment= 3,893.74

(Refer appendix)
iii) the amount of $X, if - instead of the above - Battlers Bank agrees that
Ray and Betty will repay the loan by paying the bank $3,300 per month
for the first 12 months, then $3,750 a month for the next 12 months, and
after that $X per month for the balance of the 20 year term.
Answer:
The revised loan amount to be taken for calculating the amount of X will
be $ 570184.82 and interest rate will be 4.8%.
Amount of installment= $ 570184.82/ Cumulative present value factor @
4.8%
The amount of X= 570184.82/ 144.45
Hence X= 3,947.28
(Refer Appendix)
iv) how long (in years and months) it would take to repay the loan if,
alternatively, Ray and Betty decide to repay $3,500 per month, with the
first repayment again being at the end of the first month after taking the
loan, and continuing until the loan was repaid.
Answer:
Loan amount: $600000
Installment= $3500/Month
Interest= 4.8%
Hence, the no. of years required to repay the loan= 24.17 years
We can say 24 Years and 2 months.
(Refer Appendix)
v) under option iv) above, the amount of the final repayment. [NOTE:
Towards the end of the loan repayment period, after the final full monthly
instalment of $3,500 is paid, a lesser amount is likely to be outstanding.
That amount, plus interest to the end of the following month, is the final
loan repayment amount.]
Answer:
The extra amount to be paid over and above the
loan amount is $ 204.23
Hence, the amount of final repayment $ 6,00,204.23
4

QUESTION 3. [(2 + 2 + 3 + 3 + 3 + 3 = 16 marks]
This question relates to alternative investment choice techniques
Laurel Hardy is considering the following cash flows for two mutually exclusive
projects.
Year Cash Flows, Investment X ($) Cash Flows, Investment Y ($)
0 -42,000 -42,000
1 12,000 18,000
2 18,000 18,000
3 27,000 18,000
You are required to answer the following questions:
i) If the cash flows after year 0 occur evenly over each year, what is the
payback period for each project, and on this basis, which project would
you prefer?
Year Cash Flows X Cash Flows Y
0 -42000 -42000
1 12000 18000
2 18000 18000
3 27000 18000
As given in the question the cash flows occur evenly. So, we take the average
of cash flows for project X and project Y cash flows are already even.
Average =
(12000+18000+27000)
/3 57000
Average Cash flows 19000
Payback
Period(Years) 2.21 2.33
Hence, project X will be preferred over project Y.
IN THE REMAINING PARTS, ASSUME THAT ALL CASH FLOWS
OCCUR AT THE END OF EACH YEAR.
ii) Would the payback periods then be any different to your answer in i)? If
so, what would the payback periods be?
Year
Cash Flows
X
Cumulative Cash
Flows
Cash Flows
Y
0 -42000 -42000 -42000
1 12000 -30000 18000
2 18000 -12000 18000
3 27000 15000 18000
Payback
Period(Years) 2.44 2.33
5

In this case the cash flows are even and hence, the payback period of
project X increased.
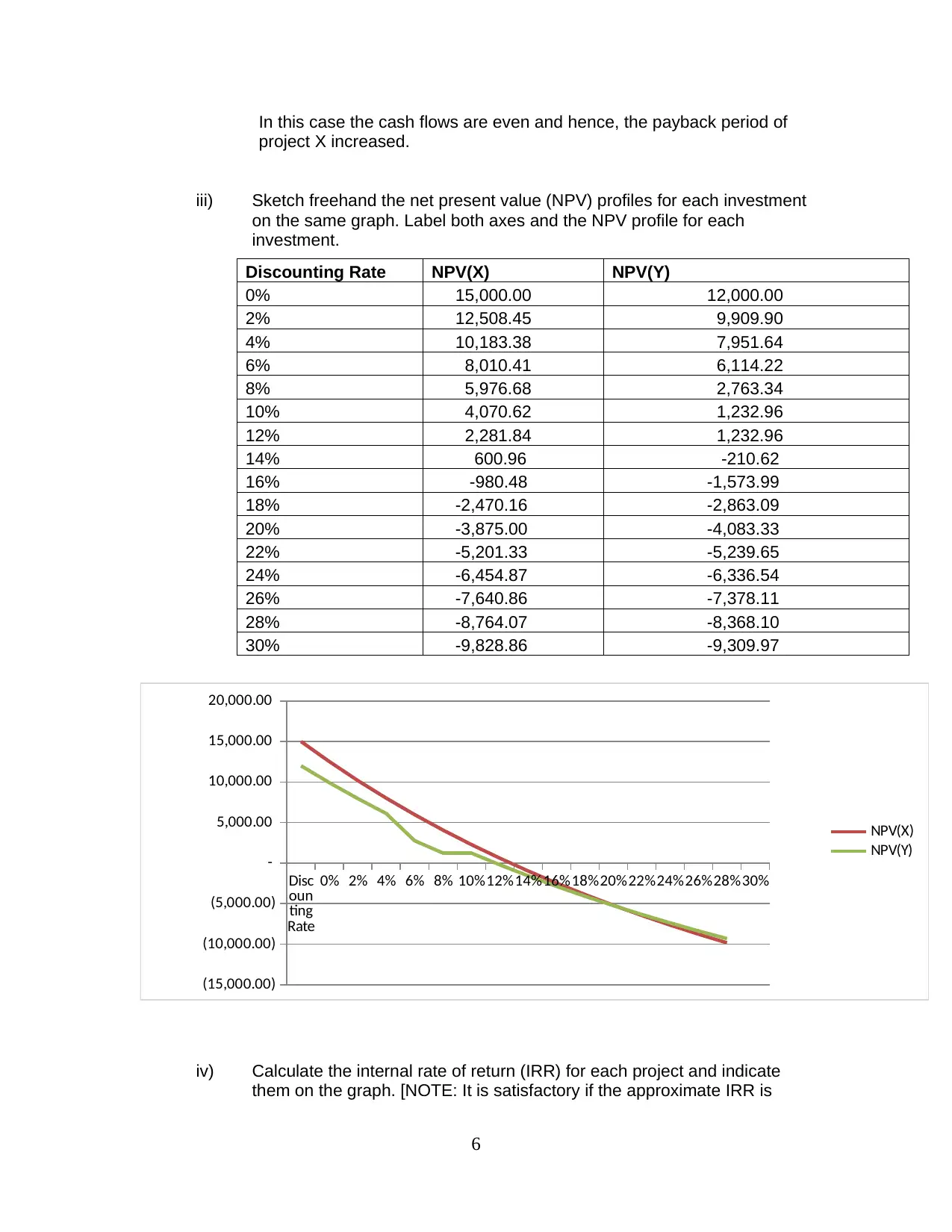
iii) Sketch freehand the net present value (NPV) profiles for each investment
on the same graph. Label both axes and the NPV profile for each
investment.
Disc
oun
ting
Rate
0% 2% 4% 6% 8% 10%12%14%16%18%20%22%24%26%28%30%
(15,000.00)
(10,000.00)
(5,000.00)
-
5,000.00
10,000.00
15,000.00
20,000.00
NPV(X)
NPV(Y)
iv) Calculate the internal rate of return (IRR) for each project and indicate
them on the graph. [NOTE: It is satisfactory if the approximate IRR is
6
Discounting Rate NPV(X) NPV(Y)
0% 15,000.00 12,000.00
2% 12,508.45 9,909.90
4% 10,183.38 7,951.64
6% 8,010.41 6,114.22
8% 5,976.68 2,763.34
10% 4,070.62 1,232.96
12% 2,281.84 1,232.96
14% 600.96 -210.62
16% -980.48 -1,573.99
18% -2,470.16 -2,863.09
20% -3,875.00 -4,083.33
22% -5,201.33 -5,239.65
24% -6,454.87 -6,336.54
26% -7,640.86 -7,378.11
28% -8,764.07 -8,368.10
30% -9,828.86 -9,309.97

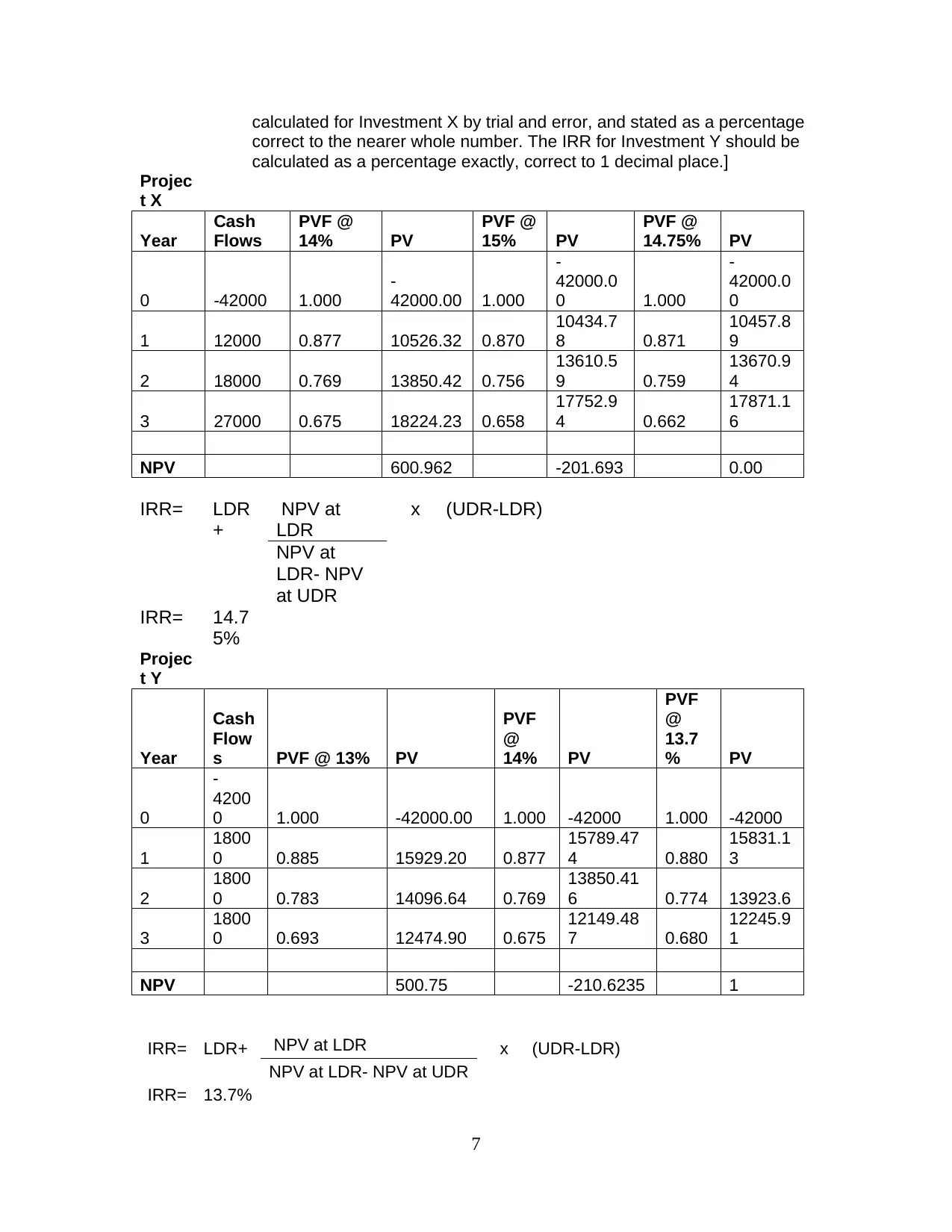
calculated for Investment X by trial and error, and stated as a percentage
correct to the nearer whole number. The IRR for Investment Y should be
calculated as a percentage exactly, correct to 1 decimal place.]
Projec
t X
Year
Cash
Flows
PVF @
14% PV
PVF @
15% PV
PVF @
14.75% PV
0 -42000 1.000
-
42000.00 1.000
-
42000.0
0 1.000
-
42000.0
0
1 12000 0.877 10526.32 0.870
10434.7
8 0.871
10457.8
9
2 18000 0.769 13850.42 0.756
13610.5
9 0.759
13670.9
4
3 27000 0.675 18224.23 0.658
17752.9
4 0.662
17871.1
6
NPV 600.962 -201.693 0.00
IRR= LDR
+
NPV at
LDR
x (UDR-LDR)
NPV at
LDR- NPV
at UDR
IRR= 14.7
5%
Projec
t Y
Year
Cash
Flow
s PVF @ 13% PV
PVF
@
14% PV
PVF
@
13.7
% PV
0
-
4200
0 1.000 -42000.00 1.000 -42000 1.000 -42000
1
1800
0 0.885 15929.20 0.877
15789.47
4 0.880
15831.1
3
2
1800
0 0.783 14096.64 0.769
13850.41
6 0.774 13923.6
3
1800
0 0.693 12474.90 0.675
12149.48
7 0.680
12245.9
1
NPV 500.75 -210.6235 1
IRR= LDR+ NPV at LDR x (UDR-LDR)
NPV at LDR- NPV at UDR
IRR= 13.7%
7

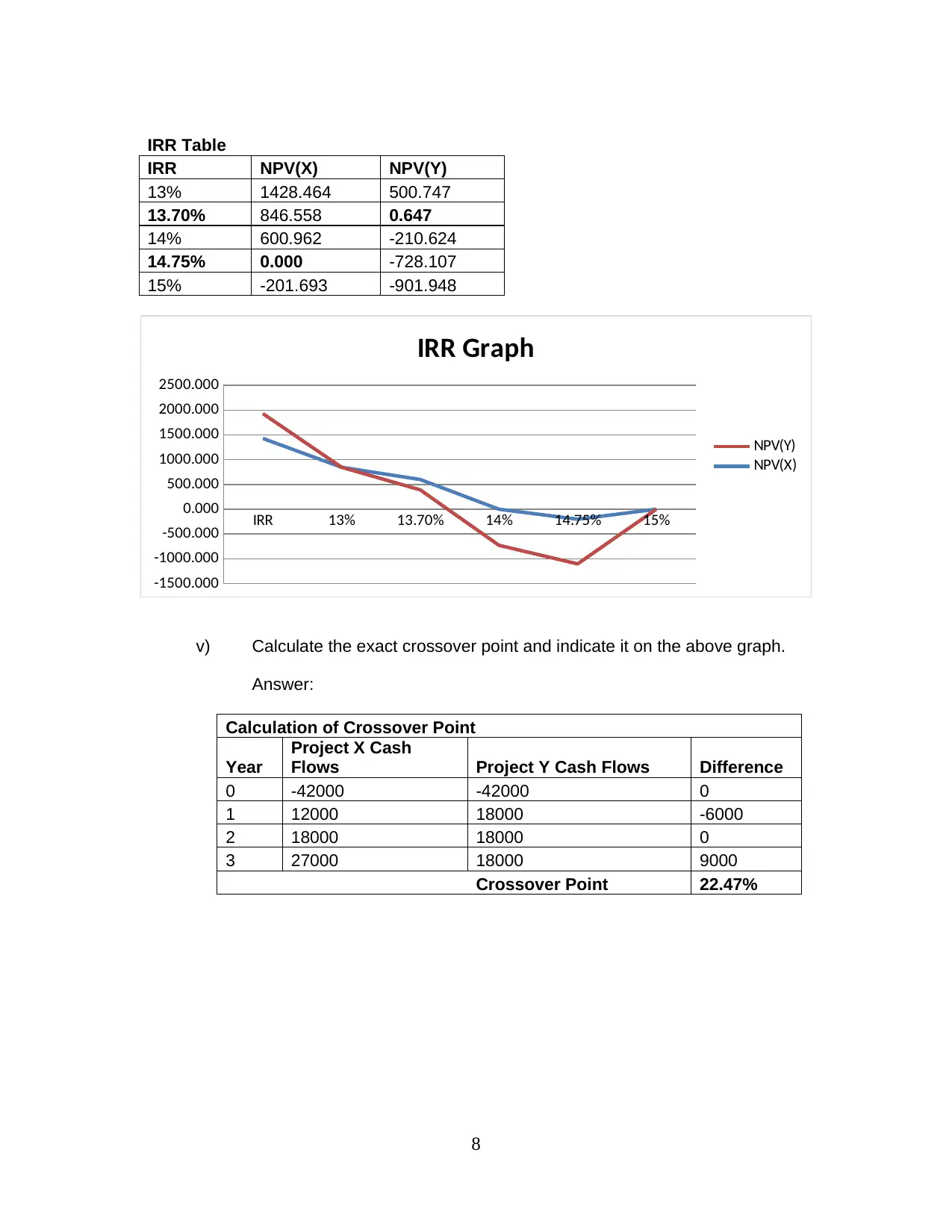
IRR Table
IRR NPV(X) NPV(Y)
13% 1428.464 500.747
13.70% 846.558 0.647
14% 600.962 -210.624
14.75% 0.000 -728.107
15% -201.693 -901.948
IRR 13% 13.70% 14% 14.75% 15%
-1500.000
-1000.000
-500.000
0.000
500.000
1000.000
1500.000
2000.000
2500.000
IRR Graph
NPV(Y)
NPV(X)
v) Calculate the exact crossover point and indicate it on the above graph.
Answer:
Calculation of Crossover Point
Year
Project X Cash
Flows Project Y Cash Flows Difference
0 -42000 -42000 0
1 12000 18000 -6000
2 18000 18000 0
3 27000 18000 9000
Crossover Point 22.47%
8

Dis
cou
nti
ng
Rat
e
0% 2% 4% 6% 8% 10
% 12
% 14
% 16
% 18
% 20
% 22
% 24
% 26
% 28
% 30
%
(15,000.00)
(10,000.00)
(5,000.00)
-
5,000.00
10,000.00
15,000.00
20,000.00
NPV(X)
NPV(Y)
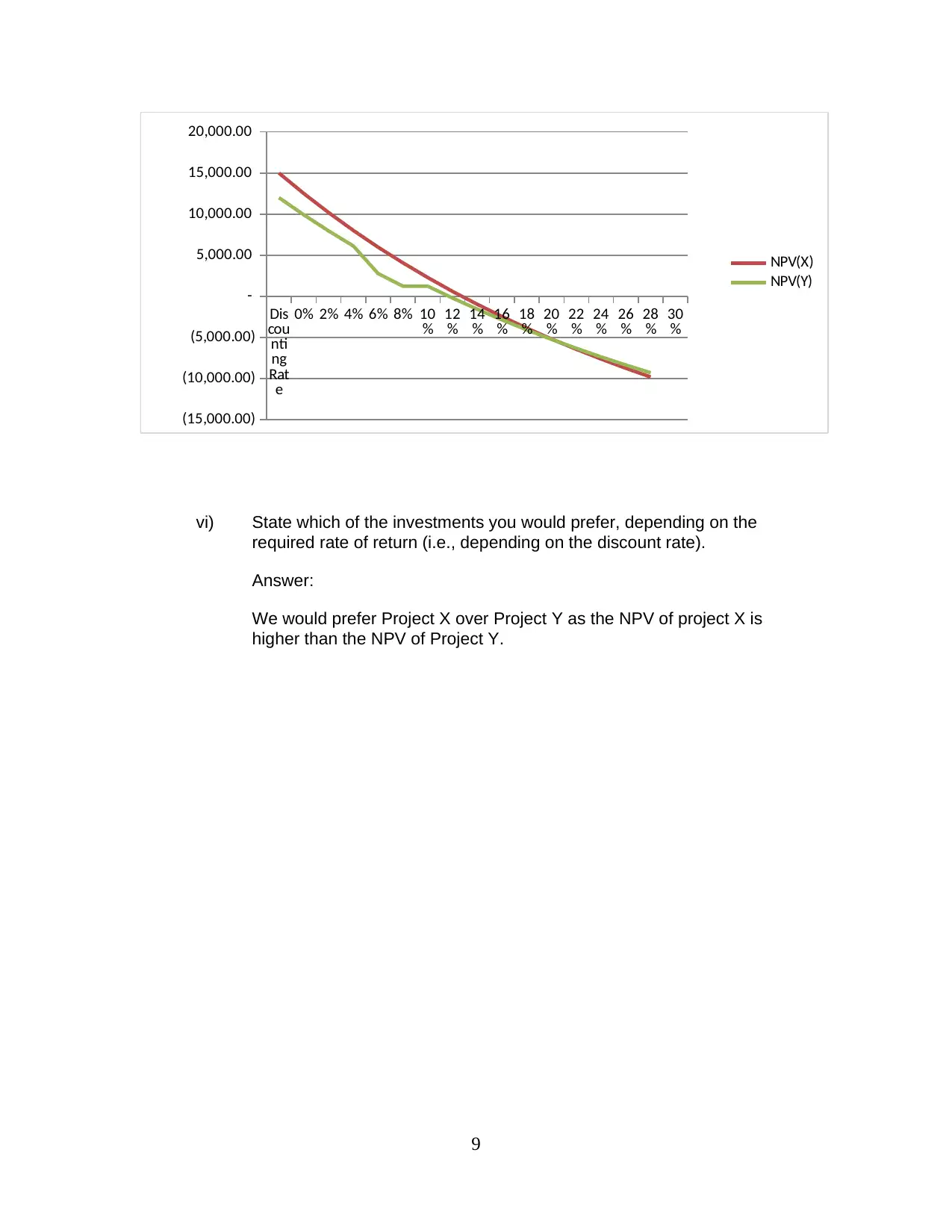
vi) State which of the investments you would prefer, depending on the
required rate of return (i.e., depending on the discount rate).
Answer:
We would prefer Project X over Project Y as the NPV of project X is
higher than the NPV of Project Y.
9

QUESTION 4. [18 + 2 = 20 marks].
This question relates to capital budgeting.
Diana Deall Ltd is considering the purchase of new technology costing $700,000, which
it will fully finance with a fixed interest loan of 10% per annum, with the principal repaid
at the end of 4 years.
The new technology will permit the company to reduce its to reduce its labour costs by
$250,000 a year for 4 years, and the technology may be depreciated for tax purposes by
the straight-line method to zero over the 4 years. The company thinks that it can sell the
technology at the end of 4 years for $40,000.
The technology will need to be stored in a building, currently being rented out for
$35,000 a year under a lease agreement with 4 yearly rental payments to run, the next
one being due at the end of one year. Under the lease agreement, Diana Deall Ltd can
cancel the lease by paying the tenant (now) compensation equal to one year’s rental
payment plus 10%, but this amount is not deductible for income tax purposes.
This is not the first time that the company has considered this purchase. Twelve months
ago, the company engaged Fairgo Consultants, at a fee of $25,000 paid in advance, to
conduct a feasibility study on savings strategies and Fairgo made the above
recommendations. At the time, Diana Deall did not proceed with the recommended
strategy, but is now reconsidering the proposal.
Diana Deall further estimates that it will have to spend $30,000 in 2 years’ time
overhauling the technology. It will also require additions to current assets of $40,000 at
the beginning of the project, which will be fully recoverable at the end of the fourth year.
Diana Deall Ltd’s cost of capital is 12%. The tax rate is 30%. Tax is paid in the year in
which earnings are received.
REQUIRED:
(a) Calculate the net present value (NPV), that is, the net benefit or net loss in
present value terms of the proposed purchase costs and the resultant
incremental cash flows.
[HINT: As shown in the text-book, it is recommended that for each year you
calculate the tax effect first, then identify the cash flows, then calculate the
overall net present value.]
Answer:
Year
Labou
r Cost
Depreciat
ion
Overha
uling
Cost Interest PBT
Tax
@
30% PAT
Cash
Flows
PVF @
12% PV
0 -740000 1 -740000
1
25000
0 165000 0 70000 15000 4500 10500 175500 0.893 1,56,696.43
2
25000
0 165000 30000 70000 -15000 -4500 -10500 154500 0.797 1,23,166.45
3
25000
0 165000 0 70000 15000 4500 10500 175500 0.712 1,24,917.43
4
25000
0 165000 0 70000 15000 4500 10500 175500 0.636 1,11,533.42
4 Resale Value net of Tax 28000 0.636 17,794.51
4 Working capital 40000 0.636 25,420.72
NPV -1,80,471.03
10

Notes:
Cost of technology 700000
Resale value 40000
Depreciation 165000
Interest 70000
Initial Investment
Cost of
Technology 700000
Add: Working
Capital 40000
Initial Investment 740000
(b) Should the company purchase the technology? State clearly why or why not.
Answer:
The company should not purchase the technology as the NPV of the investment
is negative that means it is not profitable to invest in the project.
References:
Erickson, K. H. (2013). Investment Appraisal: A Simple Introduction, K. H. Erickson.
Herbst, A. F. (2003). Capital asset Investment: Strategy, Tactics and Tools, John Wiley
& Sons, England.
Osborne, M. (2014). Multiple Interest Rate Analysis: Theory and Applications, Springer.
11

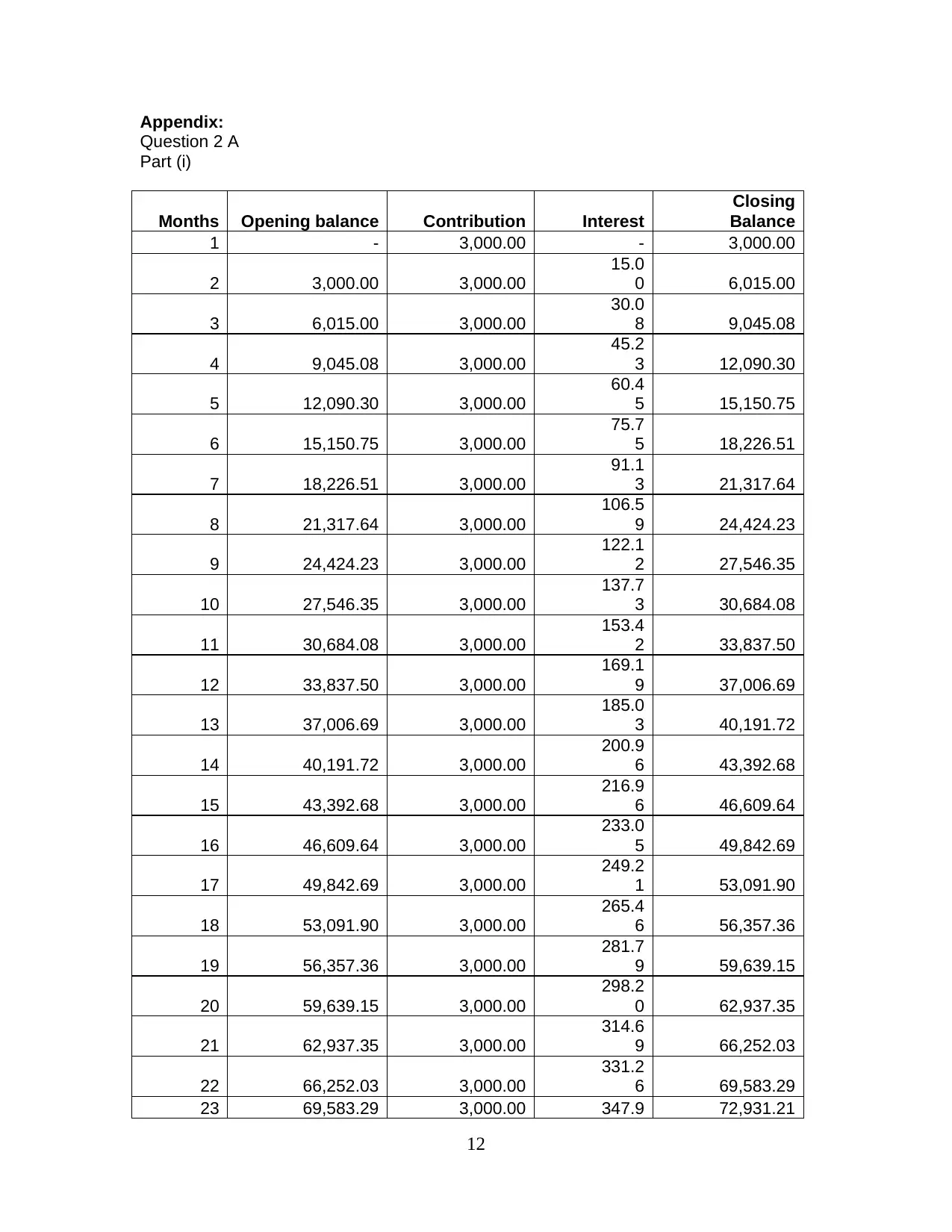
Appendix:
Question 2 A
Part (i)
Months Opening balance Contribution Interest
Closing
Balance
1 - 3,000.00 - 3,000.00
2 3,000.00 3,000.00
15.0
0 6,015.00
3 6,015.00 3,000.00
30.0
8 9,045.08
4 9,045.08 3,000.00
45.2
3 12,090.30
5 12,090.30 3,000.00
60.4
5 15,150.75
6 15,150.75 3,000.00
75.7
5 18,226.51
7 18,226.51 3,000.00
91.1
3 21,317.64
8 21,317.64 3,000.00
106.5
9 24,424.23
9 24,424.23 3,000.00
122.1
2 27,546.35
10 27,546.35 3,000.00
137.7
3 30,684.08
11 30,684.08 3,000.00
153.4
2 33,837.50
12 33,837.50 3,000.00
169.1
9 37,006.69
13 37,006.69 3,000.00
185.0
3 40,191.72
14 40,191.72 3,000.00
200.9
6 43,392.68
15 43,392.68 3,000.00
216.9
6 46,609.64
16 46,609.64 3,000.00
233.0
5 49,842.69
17 49,842.69 3,000.00
249.2
1 53,091.90
18 53,091.90 3,000.00
265.4
6 56,357.36
19 56,357.36 3,000.00
281.7
9 59,639.15
20 59,639.15 3,000.00
298.2
0 62,937.35
21 62,937.35 3,000.00
314.6
9 66,252.03
22 66,252.03 3,000.00
331.2
6 69,583.29
23 69,583.29 3,000.00 347.9 72,931.21
12