Advanced Finance Homework: Investment and Valuation Analysis

This document presents a comprehensive solution to a finance assignment, covering various financial concepts and calculations. The solution includes detailed calculations for net profit, dividend payouts, and growth rates. It analyzes investment decisions using annual equivalent costs, evaluates the present value of notes, and addresses retirement planning and loan repayment scenarios. The assignment also delves into capital budgeting techniques, such as payback period, net present value (NPV), profitability index (PI), and internal rate of return (IRR), to evaluate investment projects. Furthermore, the solution provides a detailed analysis of a hydrofoil investment, considering depreciation, tax implications, and cash flow analysis to determine the net present value and make informed investment recommendations. The document provides students with a valuable resource for understanding financial concepts and solving complex problems.

Solution 1
a)
Net profit of Fisher Ltd for year 2017-18 $ 800,000
Bradley Lane's Share 12%
Dividend payout ratio 70%
Growth rate in earnings 20%
Estimated profit of Fisher Ltd for year 2018-19 (800000 x (1 + 20%)) $ 960,000
Dividend to be received in late September 2018 by Bradley Lane (800000 x 12% x 70%) $ 67,200
Dividend to be received in September 2019 by Bradley Lane (960000 x 12% x 70%) $ 80,640
Amount required in late September 2019 $ 95,000
Amount to be received in late September 2019 from Dividend $ 80,640
Balance amount required $ 14,360
Interest rate 10%
Amount which can be consumed by Bradley Lane in late September 2018
= 67200 - (14360/ (1+ 10%))
= $54,145
b)
Discount rate = 6%
Cost of Van A = $70,000
Useful life (in years) = 3
Operating cost per annum = $7,000
Present value factor for 3 years at 6% = 2.6730
Annual Equivalent cost for Van A = (70000 / 2.6730) + 7000
= $33,188
Cost of Van B = $90,000
Useful life (in years) = 4
Operating cost per annum = $9,000
Present value factor for 4 years at 6% = 3.4651
Annual Equivalent cost for Van B = 90000 / 3.4651 + 9000
= $34,973
Van A should be selected as annual equivalent cost for Van A is less than annual equivalent cost for
Van B.
c)

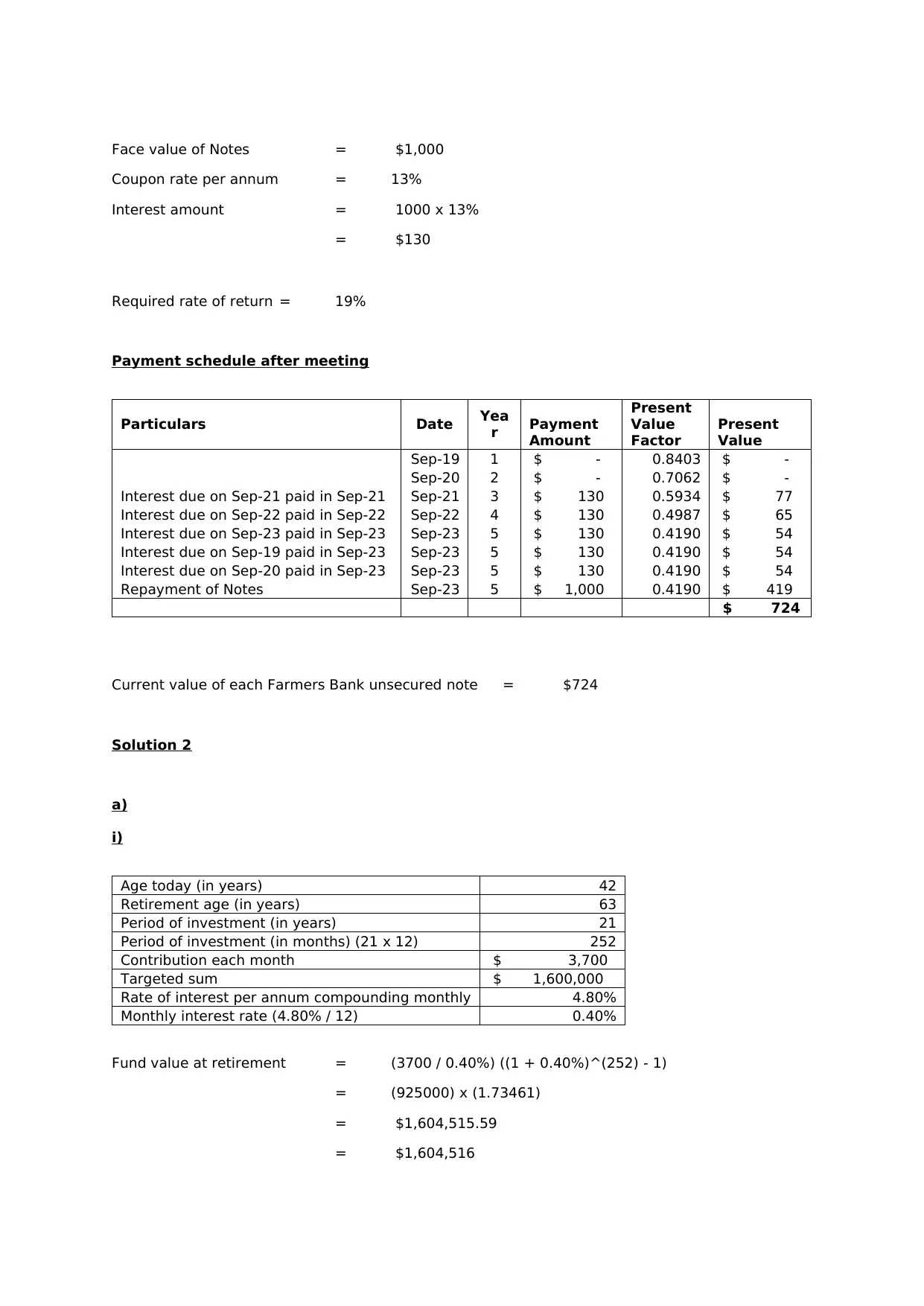
Face value of Notes = $1,000
Coupon rate per annum = 13%
Interest amount = 1000 x 13%
= $130
Required rate of return = 19%
Payment schedule after meeting
Particulars Date Yea
r Payment
Amount
Present
Value
Factor
Present
Value
Sep-19 1 $ - 0.8403 $ -
Sep-20 2 $ - 0.7062 $ -
Interest due on Sep-21 paid in Sep-21 Sep-21 3 $ 130 0.5934 $ 77
Interest due on Sep-22 paid in Sep-22 Sep-22 4 $ 130 0.4987 $ 65
Interest due on Sep-23 paid in Sep-23 Sep-23 5 $ 130 0.4190 $ 54
Interest due on Sep-19 paid in Sep-23 Sep-23 5 $ 130 0.4190 $ 54
Interest due on Sep-20 paid in Sep-23 Sep-23 5 $ 130 0.4190 $ 54
Repayment of Notes Sep-23 5 $ 1,000 0.4190 $ 419
$ 724
Current value of each Farmers Bank unsecured note = $724
Solution 2
a)
i)
Age today (in years) 42
Retirement age (in years) 63
Period of investment (in years) 21
Period of investment (in months) (21 x 12) 252
Contribution each month $ 3,700
Targeted sum $ 1,600,000
Rate of interest per annum compounding monthly 4.80%
Monthly interest rate (4.80% / 12) 0.40%
Fund value at retirement = (3700 / 0.40%) ((1 + 0.40%)^(252) - 1)
= (925000) x (1.73461)
= $1,604,515.59
= $1,604,516

Ruth Bray will have $1,604,516 at the age of retirement.
Yes, she will achieve the targeted sum.
She will have surplus = 1604516 - 1600000
= $4,516
ii)
Age today (in years) 63
Pension required till (in years) 87
Period of pension (in years) 24
Period of pension (in months) (24 x 12) 288
Rate of interest per annum compounding
monthly 4.80%
Monthly interest rate (4.80% / 12) 0.40%
Suppose the monthly pension amount be M.
(M / 0.40%)(1 - (1 + 0.40%)^(-288)) = $1,604,516
M (170.8172) = $1,604,516
M = 1604516 / 170.8172
M = $9,393
Monthly pension Joan will receive is $9,393.
b)
i)
Interest rate per annum compounding monthly = 4.50%
Monthly interest rate (4.50% / 12) = 0.375%
Effective annual interest rate = (1 + 0.375%)^12 - 1
= 4.594%
ii)
Interest rate per annum compounding monthly 4.50%
Monthly interest rate (4.50% / 12) 0.375%
Repayment period (in years) 25
Repayment period (in months) (25 x 12) 300
Amount of loan $ 750,000

Suppose month instalment size be M.
(M / 0.375%)(1 - (1 + 0.375%)^(-300)) = $750,000
M (179.9103) = $750,000
M = 750000 / 179.9103
M = $4,169
Amount of monthly repayment is $4,169.
iii)
Interest rate per annum compounding monthly 4.50%
Monthly interest rate (4.50% / 12) 0.375%
Repayment period (in years) 25
Repayment period (in months) (25 x 12) 300
Amount of loan $ 750,000
Future value of repayment of $3000 per month = (3000 / 0.375%)((1 + 0.375%)^(12) - 1)
= $36,751.86
Loan pending at the end of year 1 = 750000 (1 + 0.375%)^12 - 36,751.86
= $747,703.01
Future value of repayment of $3500 per month = (3500 / 0.375%)((1 + 0.375%)^(12) - 1)
= $42,877.17
Loan pending at the end of year 2 = 747703.01 (1 + 0.375%)^12 - 42877.17
= $739,175.19
Suppose month instalment size be M after two years.
(M / 0.375%)(1 - (1 + 0.375%)^(-23M12)) = $739,175.19
M (171.756) = $739,175.19
M = 739175.19 / 171.756

M = $4,303.64
M is $4303.64 per month.
iv)
Monthly repayment = $4,400
Suppose loan is repaid in n months.
$750,000 = (4400 / 0.375%) (1 - (1 + 0.375%)^(-n))
$750,000 = (1173333.33) (1 - (1 + 0.375%)^(-n))
750000 / (1173333.33) = (1 - (1 + 0.375%)^(-n))
0.6392 = (1 - (1 + 0.375%)^(-n))
(1 + 0.375%)^(-n) = 1 - 0.6392
(1.00375)^(-n) = 0.3608
Taking log on both sides
(-n) log 1.00375 = log 0.3608
(-n) 0.00162555828 = -0.442733471
(n) 0.00162555828 = 0.442733471
n = 0.44273347113 / 0.00162555828
n = 272.3577964
n = 272.36
Total months taken for loan repayment is 273 months (22 years 9 months).
Solution 3
i)
Yea
r
Investment P ($)
Cash flows
Cumulative Cash
Flows
0 - 60,000 - 60,000
1 20,000 - 40,000

2 30,000 - 10,000
3 44,000 34,000
34,000
Payback period (Investment P) = 2 + (10000/ 44000)
= 2.23 years
Yea
r
Investment Q ($)
Cash flows
Cumulative Cash
Flows
0 - 60,000 - 60,000
1 30,000 - 30,000
2 30,000 -
3 30,000 30,000
30,000
Payback period (Investment Q) = 2.00 years
On this basis, we should prefer Investment Q as its payback period is less than that of Investment
P.
ii)
Payback period will be different in this case.
Yea
r
Investment P ($)
Cash flows
Cumulative Cash
Flows
0 - 60,000 - 60,000
1 20,000 - 40,000
2 30,000 - 10,000
3 44,000 34,000
34,000
Payback period (Investment P) = 3.00 years
Yea
r
Investment Q ($)
Cash flows
Cumulative Cash
Flows
0 - 60,000 - 60,000
1 30,000 - 30,000
2 30,000 -
3 30,000 30,000

30,000
Payback period (Investment Q) = 2.00 years
iii)
Required rate of return = 8%
Yea
r PVF Investment P ($)
Cash flows Present Value
0 1.0000 - 60,000 - 60,000
1 0.9259 20,000 18,519
2 0.8573 30,000 25,720
3 0.7938 44,000 34,929
34,000 19,167
NPV of Investment P = $19,167.30
Profitability Index of Investment P = (18519+25720+34929) / 60000
= 1.32
Yea
r PVF Investment Q ($)
Cash flows Present Value
0 1.0000 - 60,000 - 60,000
1 0.9259 30,000 27,778
2 0.8573 30,000 25,720
3 0.7938 30,000 23,815
30,000 17,313
NPV of Investment Q = $17,312.91
Profitability Index of Investment Q = (27778 + 25720 + 23815) / 60000
= 1.29
iv)
An estimate of IRR can be made using NPV profiling of both the investments.

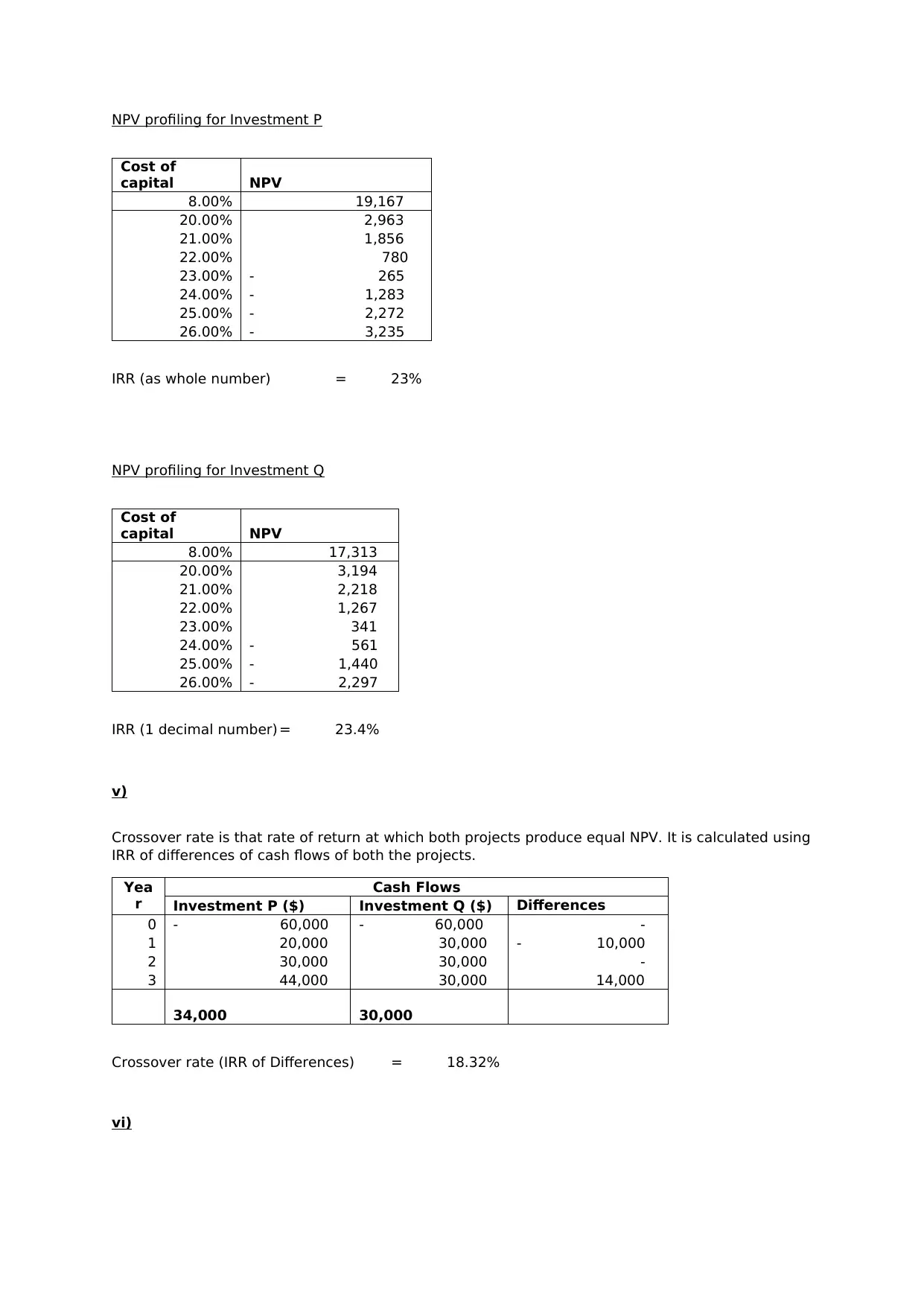
NPV profiling for Investment P
Cost of
capital NPV
8.00% 19,167
20.00% 2,963
21.00% 1,856
22.00% 780
23.00% - 265
24.00% - 1,283
25.00% - 2,272
26.00% - 3,235
IRR (as whole number) = 23%
NPV profiling for Investment Q
Cost of
capital NPV
8.00% 17,313
20.00% 3,194
21.00% 2,218
22.00% 1,267
23.00% 341
24.00% - 561
25.00% - 1,440
26.00% - 2,297
IRR (1 decimal number) = 23.4%
v)
Crossover rate is that rate of return at which both projects produce equal NPV. It is calculated using
IRR of differences of cash flows of both the projects.
Yea
r
Cash Flows
Investment P ($) Investment Q ($) Differences
0 - 60,000 - 60,000 -
1 20,000 30,000 - 10,000
2 30,000 30,000 -
3 44,000 30,000 14,000
34,000 30,000
Crossover rate (IRR of Differences) = 18.32%
vi)

Summary of results
Criteria
Payback
period NPV PI IRR
Investment P 2.23 $19,167.30 1.32 22.75%
Investment Q 2.00 $17,312.91 1.29 23.38%
The main objective of any organization is to maximize shareholders' wealth.
Payback period - As per payback period criteria, Project Q should be selected as Project Q has
lower payback period.
NPV (Net Present Value) - As per NPV criteria - Project P should be selected as Project P has higher
NPV.
PI (Profitability Index) - As per Profitability Index criteria - Project P should be select as Project P has
higher PI.
IRR (Internal Rate of Return) - As per IRR criteria, Project Q should be selected as Project Q has
higher IRR.
NPV is preferred over payback period because:
a) Payback period ignores time value of money and cash flows occurring after payback
period.
b) It ignores time value of money.
NPV will be preferred over the payback period and IRR because assumption of IRR that returns will
be reinvestment at the rate equal to IRR is not true in real world.
Generally NPV and PI both give same results.
Due to above reasons, we accept the recommendation of NPV and project P should be selected.
Solution 4
a)
Cost of each hydrofoils $ 480,000
Total cost of hydrofoils (480000 x 2) $ 960,000
Tax rate 30%
Cost of capital 11%
Savings in energy and labour costs $ 160,000
Useful life of new hydrofoils (in years) 4
Depreciation on each hydrofoils (480000 / 4) $ 120,000
Depreciation for both the hydrofoils (120000 x 2) $ 240,000

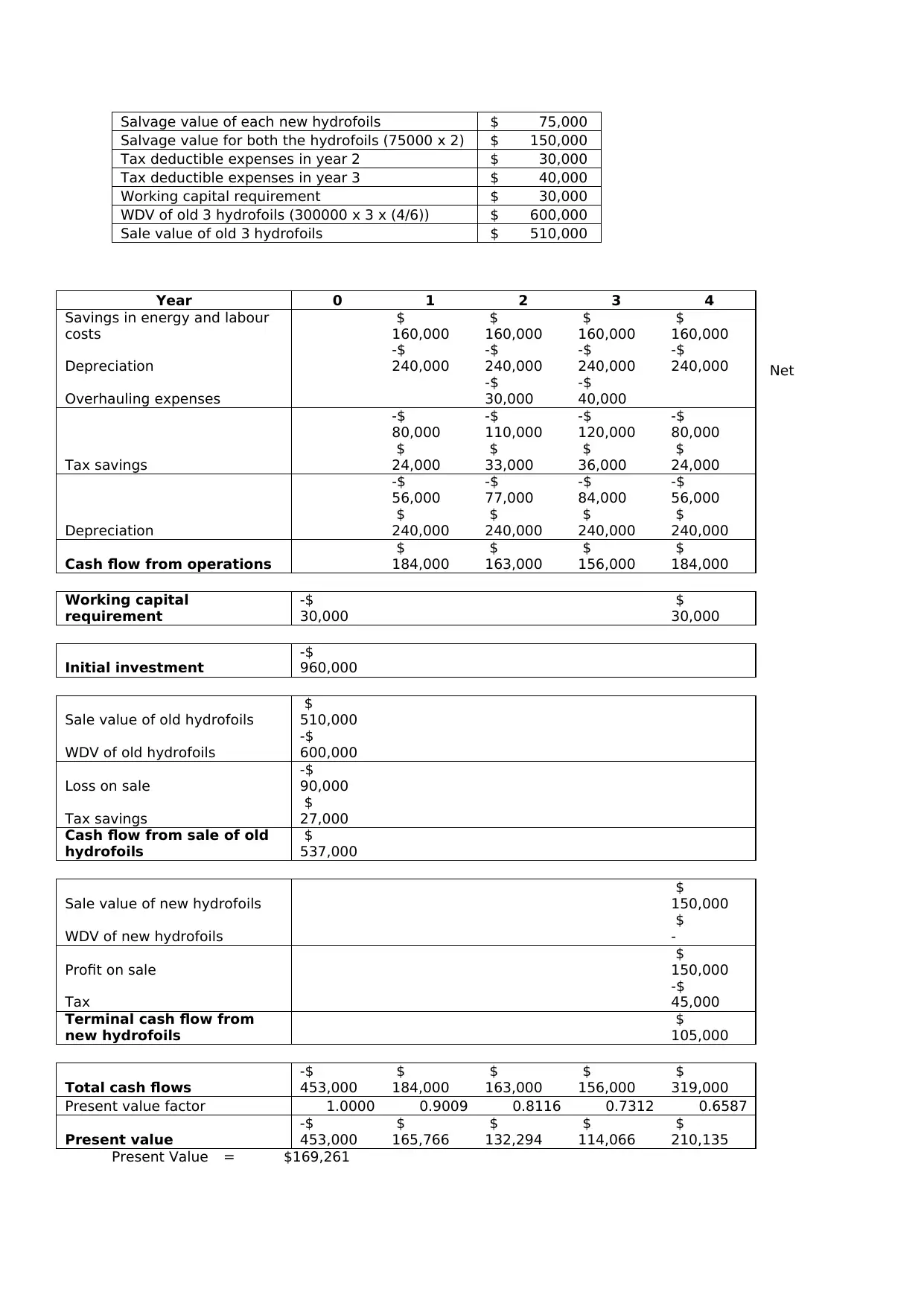
Salvage value of each new hydrofoils $ 75,000
Salvage value for both the hydrofoils (75000 x 2) $ 150,000
Tax deductible expenses in year 2 $ 30,000
Tax deductible expenses in year 3 $ 40,000
Working capital requirement $ 30,000
WDV of old 3 hydrofoils (300000 x 3 x (4/6)) $ 600,000
Sale value of old 3 hydrofoils $ 510,000
Net
Present Value = $169,261
Year 0 1 2 3 4
Savings in energy and labour
costs
$
160,000
$
160,000
$
160,000
$
160,000
Depreciation
-$
240,000
-$
240,000
-$
240,000
-$
240,000
Overhauling expenses
-$
30,000
-$
40,000
-$
80,000
-$
110,000
-$
120,000
-$
80,000
Tax savings
$
24,000
$
33,000
$
36,000
$
24,000
-$
56,000
-$
77,000
-$
84,000
-$
56,000
Depreciation
$
240,000
$
240,000
$
240,000
$
240,000
Cash flow from operations
$
184,000
$
163,000
$
156,000
$
184,000
Working capital
requirement
-$
30,000
$
30,000
Initial investment
-$
960,000
Sale value of old hydrofoils
$
510,000
WDV of old hydrofoils
-$
600,000
Loss on sale
-$
90,000
Tax savings
$
27,000
Cash flow from sale of old
hydrofoils
$
537,000
Sale value of new hydrofoils
$
150,000
WDV of new hydrofoils
$
-
Profit on sale
$
150,000
Tax
-$
45,000
Terminal cash flow from
new hydrofoils
$
105,000
Total cash flows
-$
453,000
$
184,000
$
163,000
$
156,000
$
319,000
Present value factor 1.0000 0.9009 0.8116 0.7312 0.6587
Present value
-$
453,000
$
165,766
$
132,294
$
114,066
$
210,135

b)
Company should buy new hydrofoils as Net Present Value (NPV) is positive.