Financial Calculations: Analysis of Time Value of Money and Loans

This assignment delves into various financial calculations, including the time value of money, compound interest, and depreciation. The introduction explains the core concept of time value of money and its impact on investment decisions. The main body of the assignment provides detailed solutions to several questions. Question 15 involves compound interest calculations, determining future values, interest rates, and time periods. Question 16 analyzes a disagreement between two individuals on the time required for an investment to grow, highlighting the importance of correct compounding frequency. Question 17 covers interest rate calculations, EMI calculations, and annuity calculations. Question 21 focuses on loan calculations, including EMI and total cost analysis under different repayment scenarios. Finally, question 23 demonstrates depreciation calculations using the reducing balance method. The conclusion summarizes the significance of the time value of money in evaluating investment opportunities and the impact of interest rates and compounding periods. The document references various books and journals to support its analysis.

FINANCIAL CALCULATIONS

TABLE OF CONTENTS
INTRODUCTION...........................................................................................................................1
MAIN BODY...................................................................................................................................1
QUESTION- 15...............................................................................................................................1
Compound interest calculations...................................................................................................1
QUESTION- 16...............................................................................................................................2
QUESTION- 17...............................................................................................................................3
QUESTION- 21...............................................................................................................................4
QUESTION- 23...............................................................................................................................4
Calculation of depreciation..........................................................................................................4
CONCLUSION................................................................................................................................4
REFERENCES................................................................................................................................5

INTRODUCTION
Time value of money is the crucial concept representing the fact that the money that is
now possessed with the person is of higher value comparatively as it has the better earning
capacity than the same amount possessed in the future. The time value of money shall be
decreasing its worth as it has opportunity cost that is being forgone in that case. The rate at
which the future value is discounted also depends on the opportunity cost that is attached with
the sum of money. In the current project the report shall be demonstrating the various
calculations pertaining to the time value of money and annuity calculations to develop the better
understanding of the project. Apart from that it shall also be representing the calculations related
to the compound of interest over yearly, quarterly, monthly and daily basis.
MAIN BODY
QUESTION- 15
Compound interest calculations
a) Present value= 5000
Rate of interest= 8%
Time period= 5 years
Future value= ?
Future value= Present value * (1 + r) t
= 5000 * (1 + 0.08) 5
= 7346.64
Future value= 7346.64
b) Present value= 7000
Future value= 14000
Time period= 8 years
Rate of interest= ?
Future value= Present value * (1 + r) t
14000= 7000 * (1 + x) 8
14000 / 7000= 2
In the future value factor table the value 2 is seen at the 8 years and so we get the interest rate to
be 9.22% which is rounded off to 9%.
Interest rate= 9%
1

c) Present value= 9000
Future value= 18000
Rate of interest= 6%
Time period= ?
Future value= Present value * (1 + r) t
18000 / 9000= 2
By referring to the future value factor table it can be assessed that at the interest rate of 6% the
value is at 12 years. The value is 2.012.
Time period= 12 years
QUESTION- 16
Present value= 1000
Future value= 1814.02
Rate of interest= 6%
Time period= ?
The interest rate is compounded quarterly
Effective interest rate= 6% / 4 = 1.5% per quarter
Time period= n*4
Correct calculation
As per Karen the calculation was undertaken by taking the effective interest rate and the time
period was calculated per quarter and then it was converted yearly.
Future value= Present value * (1 + r) t
1814.02= 1000 * (1 + 0.015) n*4
n= 10 years
This calculation can be considered correct as the rate of interest shall depend on the number of
compounding that are made yearly.
Incorrect calculation
As per Ben the calculation was made by directly undertaking the rate of the interest that is given
without changing as per number of compounding per quarter. This is taken by referring to the
future value factor table s given below :-
1814.02 / 1000= 1.81402
In the given table this value is found out at 6% per annum and the values assessed are
2

10 years- 1.791
11 years- 1.898
Difference= 1.898 – 1.791= 0.107
1 / 0.107 * (1.81402 – 1.791)
1 / 0.107 * 0.02302
= 0.22
Number of years= 10.22 years
This calculation is considered to be wrong since the interest rate is taken as a whole
rather than adjusting it according to the quarterly compounding that is been undertaken. If the
compounding is done quarterly then the interest rate is to be divided by 4, if it is undertaken
monthly then the interest rate is divided by 12 and if the same is undertaken daily then the
interest rate shall be multiplied by 365 (Clark and et.al., 2018). Similarly, in all these cases the
time period shall be multiplied with the same number accordingly. So it can be considered that
the calculation made by Karen are correct and verified as per the arithmetic accuracy.
QUESTION- 17
a) Present value= 2000
Future value= 2960.49
Time period= 5 years
Rate of interest= x
Since the compounding is done twice a year which is semi-annually so the time period will be
multiplied by 2 and the interest rate shall be divided by 2 (Shang and Haberman, 2020).
So,
Time period= 10 semesters
Rate of interest = x / 2
Future value= Present value * (1 + r) ^ t
2960.49= 2000 * (1 + x/2 ) ^ 10
2960.49 / 2000= 1.480
x / 2= 4%
x= 8%
b) EMI= [P * R * ( 1 + R ) ^ n] / ( 1 + R ) ^ n-1
p= principle amount
3

R= rate of interest
n= time period
EMI= 4000
Rate of interest= 9%
Compounded semi-annually= 9 / 2= 4.5%
Time period= 20 years
Compounded semi-annually= 20 * 2= 40 semesters
4000= [P * 0.045 * (1 + 0.045 ) ^ 40 / ( 1 + 0.045 ) ^ 40-1
P= 85061
The principle amount of loan borrowed= 85061
c) Future value= Total deposits * (1 + R / 12) ^ 120
57509.67= 250 *120 * ( 1 + R / 100 * 12) ^ 120
R= 6.5%
Effective rate of interest= 6.5 / 12= 0.5416%
d) Annuity= 10000
Rate of interest = 9%
Time period = 10 years
P = PMT x ((1 – (1 / (1 + r) ^ -n)) / r)
= 10000 * (( 1 – (1 / (1 + 0.09) ^ - 10)) / 0.09
= 64176.58
QUESTION- 21
Principle amount= 30000
Rate of interest = 12% pa
Effective rate = 1% monthly
Time period= 10 years
Effective time= 120 months
EMI= [P * R * ( 1 + R ) ^ n] / ( 1 + R ) ^ n-1
EMI= [(30000 * 1% (1 + 1%) ^ 120] / (1 + 1%) ^ 120 – 1
EMI= 430.41
4

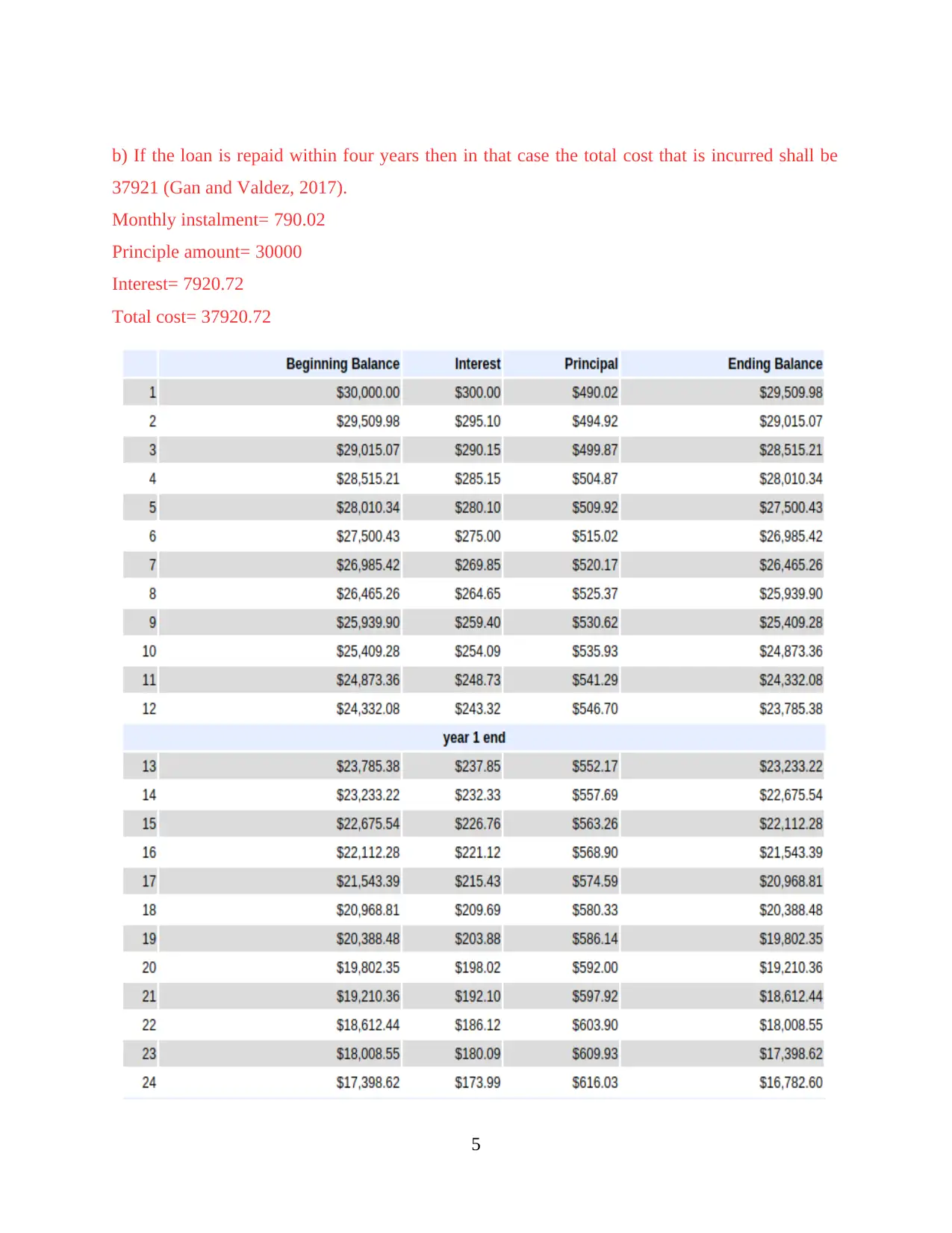
b) If the loan is repaid within four years then in that case the total cost that is incurred shall be
37921 (Gan and Valdez, 2017).
Monthly instalment= 790.02
Principle amount= 30000
Interest= 7920.72
Total cost= 37920.72
5

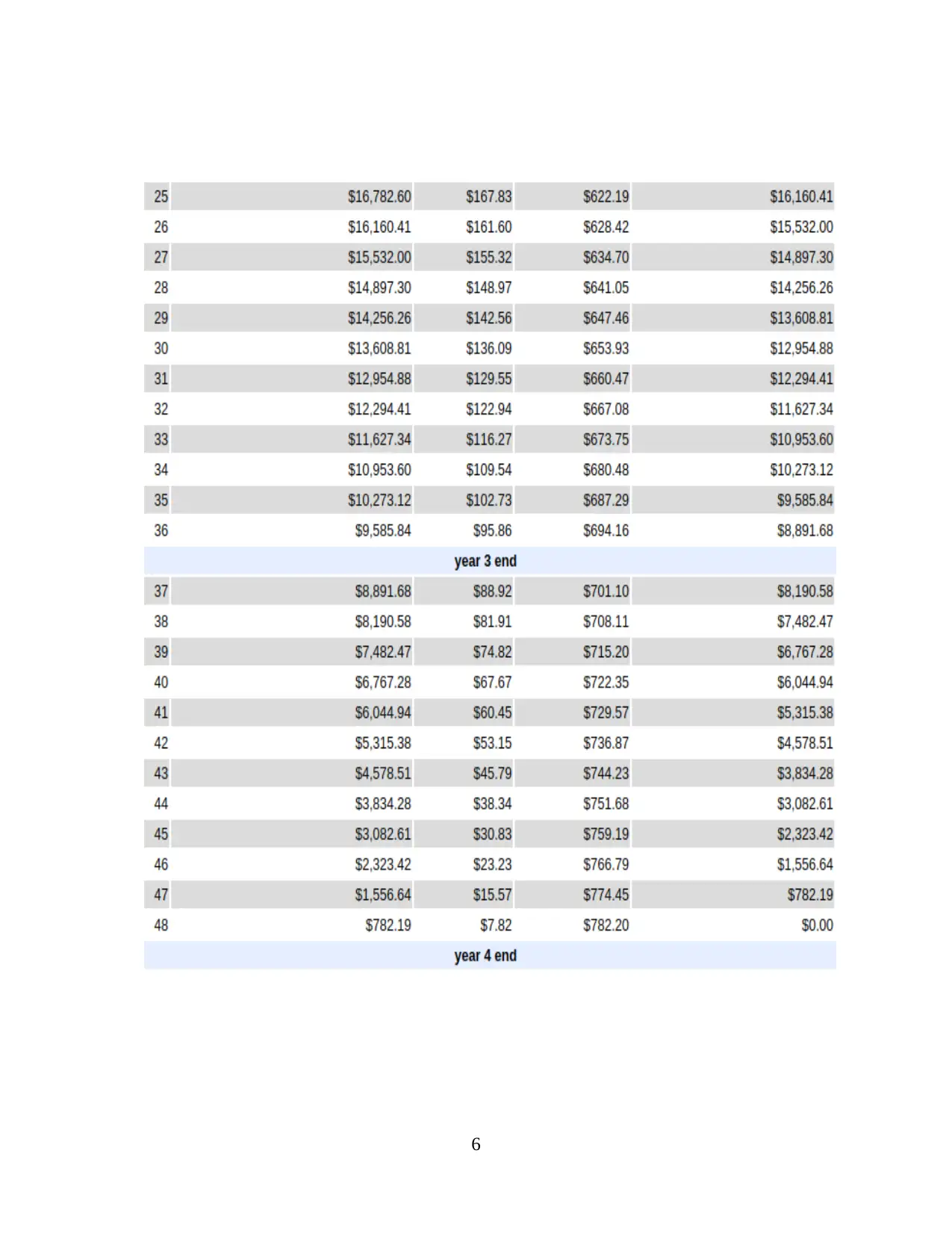
6

c) On the other hand there shall be saving in the amount of interest which shall be equal to
13728.
Interest if the loan was paid in 10 years= (430.41 * 120) – 30000
= 21649.2
Interest cost if the loan is repaid in 4 years= 7920.72
Net saving= 21649.2 – 7920.72
= 13728.48
QUESTION- 23
Calculation of depreciation
Cost of plant= 16000 on 1st July 2015
Depreciation method= Reducing balance method
Rate of depreciation= 25%
Depreciation for the period of 2015-16
16000 * 25%= 4000
Opening written down value on 30th June 2016
Cost of plant – Value of depreciation (Foster and Skoog, 2018)
16000 – 4000= 12000
Depreciation for the period of 2016-17
12000 * 25% = 3000
Opening written down value on 30th June 2017
Reduced cost of plant – Value of depreciation
12000 – 3000 = 9000
Year ending
Opening
Written Down
Value
Depreciation
Charge (for this
year)
Closing
Written Down Value
30 June 2016 $16000 4000 $16000 – 4000=
$12000
30 June 2017 $12000 3000 $12000 – 3000= $9000
7

CONCLUSION
It can be summarized from the above project that time value of money is very essential in
order to analyse an investment opportunity such that its opportunity cost can be evaluated. The
above project shows the absence of time value of money and that how a sum of amount values
higher in present due to the earning capacity as compared to the future value for the similar
amount. As the value of rupee shall be depreciating over the time that is the reason the present
value shall always be higher than the future value. The rate of interest Is also decided upon thee
discounting factor of time value of money.
8

REFERENCES
Books and Journals
Foster, E. and Skoog, G. R., 2018. Individual and Joint Life Annuities from 2014 Extended US
Life Tables. J. Legal Econ.. 24. p.107.
Gan, G. and Valdez, E. A., 2017. Valuation of large variable annuity portfolios: Monte Carlo
simulation and synthetic datasets. Dependence Modeling. 5(1). pp.354-374.
Shang, H. L. and Haberman, S., 2020. Forecasting age distribution of death counts: An
application to annuity pricing. Annals of Actuarial Science. 14(1). pp.150-169.
Shang, H. L. and Haberman, S., 2017. Grouped multivariate and functional time series
forecasting: An application to annuity pricing. Insurance: Mathematics and
Economics. 75. pp.166-179.
Clark, R. L. and et.al., 2018. Annuity options in public pension plans: the curious case of social
security leveling. The Journal of Retirement. 6(1). pp.33-44.
9