Financial Derivatives: Pricing ZCB, Forwards, Futures, Options

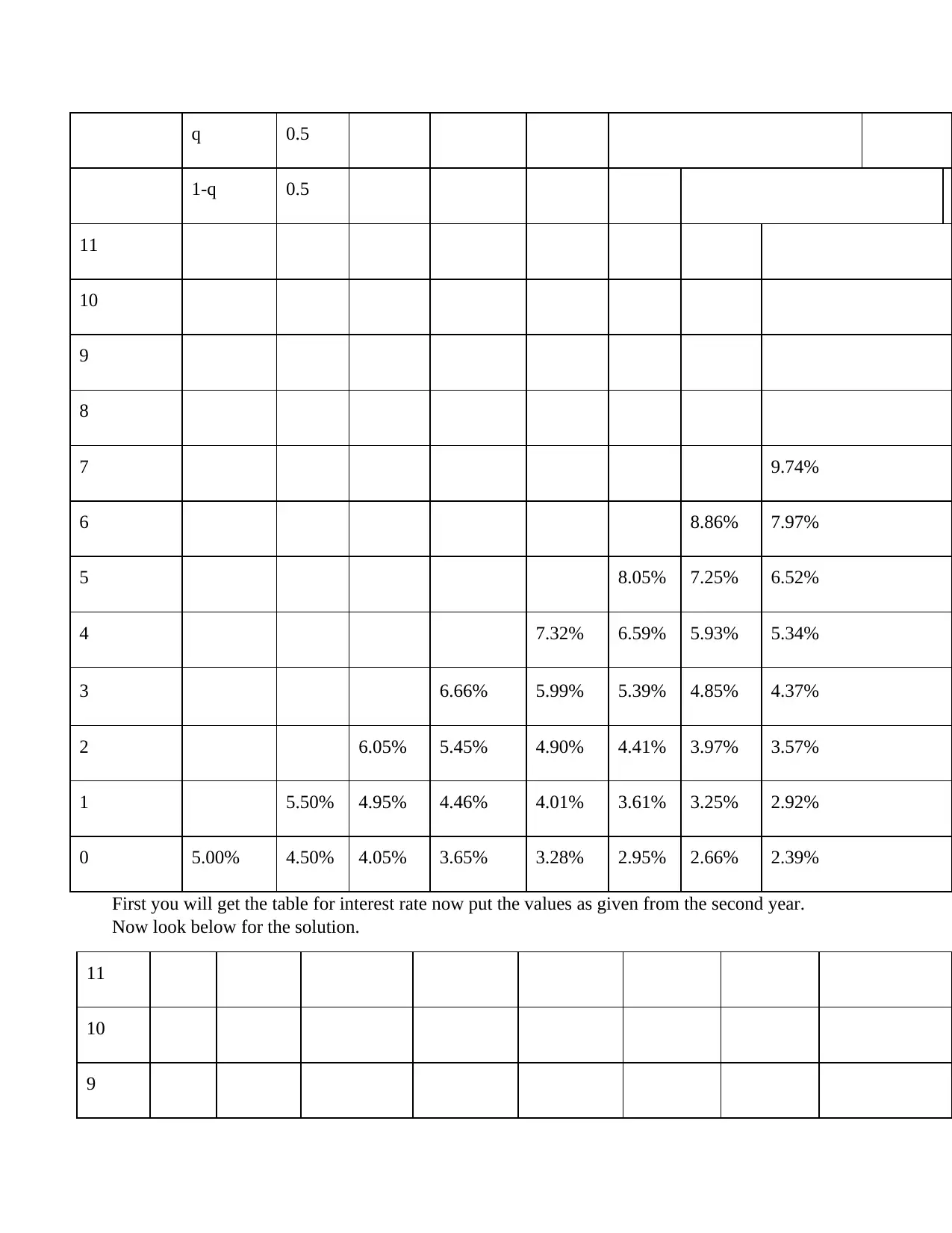
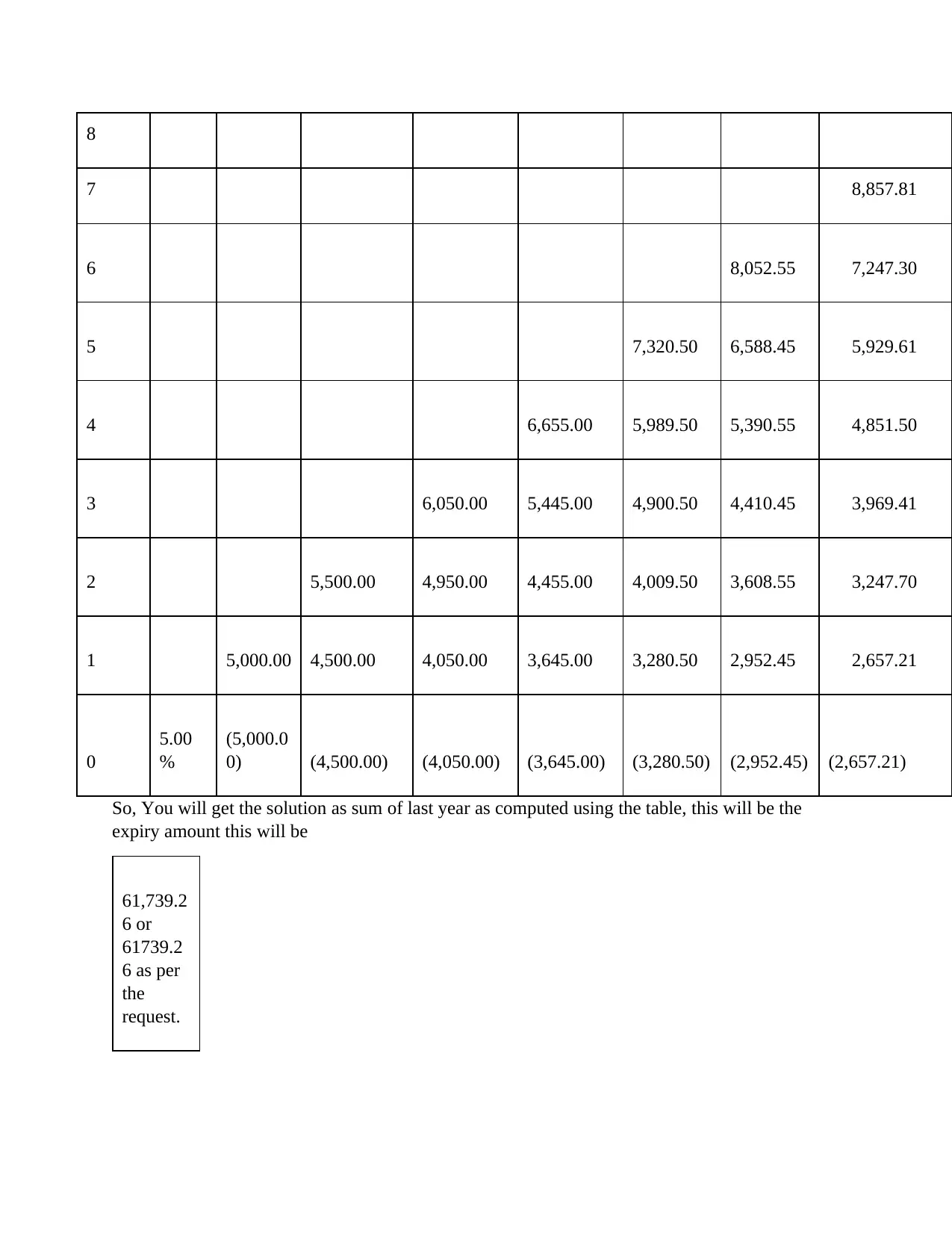
This document presents a comprehensive solution to a finance assignment focused on the valuation and pricing of various financial derivatives. The solution begins with the calculation of the price of a zero-coupon bond (ZCB) based on its face value, maturity time, and expected yield rate. It then proceeds to determine the forward price of an asset, considering spot price, maturity time, and interest rates. The assignment also explores the calculation of future prices, taking into account spot prices, carrying costs, and returns. Furthermore, the solution includes the valuation of options using the binomial option pricing model, demonstrating the calculation of option values based on up and down movements, probabilities, and risk-free rates. Finally, the assignment addresses the pricing of a fixed-rate swap using a binomial tree, providing a step-by-step approach to determine the swap's value and expiry amount. The solution incorporates the use of relevant formulas and calculations, providing a detailed and practical understanding of financial derivatives pricing.

1. Given
Face value of ZCB(F) = 100
Maturity time (t) = 10
Let we assume expected investor's required annual yield rate (r) = 10 %
price of a zero-coupon bond= P
P = F / [(1+r)^t]
hence
P=100/ [(1+.10)^10]
P= 38.55
2. Given
Spot price (P)= 38.55
Maturity time (t)= 4
(r)= 10%
So,
Forward price (A) = P*[(1+r)^t]
=38.55*[(1+.10)^4]
= 38.55*1.4641
= 56.44
3. Future price= spot price + carrying cost - returns
(a) spot price So=38.55
carring cost = So*[(1+r)^t] -- So
here r=10% and t=4
so carring cost = 17.89
returns =0 (in ZCB)

hence, initial Future price = 38.55+17.89
= 56.44
(b) spot price So=56.44
carring cost = So*[(1+r)^t] -- So
here r=10% and t=4
so carring cost = 26.19
returns =0 (in ZCB)
hence, initial Future price = 56.44+26.19
= 82.63
4. u = 1.1
d = .9
p of u = e^(r*t) - d / (u - d) = e^(.05*.5) - .9 / (1.1 - .9) = .6265
p of d = 1 - p of u = 1 - .6265 = .3734
Option value = Value of option on upside * p * e^(-r*t)
= 8*.6265 * e^(-.05*.5)
= 4.89
5. 676 answers
Fixed Rate 4.50%
Swap
expiration
Time
t=11
u 1.1
d 0.9

q 0.5
1-q 0.5
11
10
9
8
7 9.74%
6 8.86% 7.97%
5 8.05% 7.25% 6.52%
4 7.32% 6.59% 5.93% 5.34%
3 6.66% 5.99% 5.39% 4.85% 4.37%
2 6.05% 5.45% 4.90% 4.41% 3.97% 3.57%
1 5.50% 4.95% 4.46% 4.01% 3.61% 3.25% 2.92%
0 5.00% 4.50% 4.05% 3.65% 3.28% 2.95% 2.66% 2.39%
First you will get the table for interest rate now put the values as given from the second year.
Now look below for the solution.
11
10
9

8
7 8,857.81
6 8,052.55 7,247.30
5 7,320.50 6,588.45 5,929.61
4 6,655.00 5,989.50 5,390.55 4,851.50
3 6,050.00 5,445.00 4,900.50 4,410.45 3,969.41
2 5,500.00 4,950.00 4,455.00 4,009.50 3,608.55 3,247.70
1 5,000.00 4,500.00 4,050.00 3,645.00 3,280.50 2,952.45 2,657.21
0
5.00
%
(5,000.0
0) (4,500.00) (4,050.00) (3,645.00) (3,280.50) (2,952.45) (2,657.21)
So, You will get the solution as sum of last year as computed using the table, this will be the
expiry amount this will be
61,739.2
6 or
61739.2
6 as per
the
request.

6. Start at time i=10i=10.
For each node (10,j)(10,j) with j = 0,1,…,100,1,…,10, the forward price of the swap (ex
payments received at time 10) is a discounted, expected value:
S10,j=(1+r10,j)−1(12S11,j+12S11,j+1),S10,j=(1+r10,j)−1(12S11,j+12S11,j+1),
Where, for a receive fixed / pay float swap,
S10,j=1,000,000(0.045−f10,11,j)=1,000,000(0.045−r10,j).S10,j=1,000,000(0.045−f10,11,j)=1,00
0,000(0.045−r10,j).
Note that the forward rate f10,11,jf10,11,j equals r10,jr10,j on a tree where the time spacing
between the nodes matches the period for floating-rate resets and fixed rate payments.
Now find the forward swap price at each node (9,j)(9,j) with j = 0,1,…,90,1,…,9:
S9,j=(1+r9,j)−1(12S10,j+12S10,j+1+Q10,j),S9,j=(1+r9,j)−1(12S10,j+12S10,j+1+Q10,j),
Where the net payment received at time i=10i=10 is
Q10,j=1,000,000(0.045−f9,10,j)=1,000,000(0.045−r9,j).Q10,j=1,000,000(0.045−f9,10,j)=1,000,
000(0.045−r9,j).
Work your way back on the tree until you find the current swap price S0,0S0,0. Since this is a
forward starting swap beginning at time i=1i=1, do not include any net payments Q1,jQ1,j.
To price the swaption, set the terminal values at expiry i=5i=5 and j=0,1,…,5j=0,1,…,5 to
C5,j=max(S5,j,0).C5,j=max(S5,j,0).
Then work backwards from i=5i=5, calculating discounted expected values at each node until
you arrive at the current price C0,0C0,0.

References
Dai, Q., & Singleton, K. J. (2013). Specification analysis of affine term structure models. The
Journal of Finance, 55(5), 1943-1978.
Hull, J., & White, A. (2014). Numerical procedures for implementing term structure models I:
Single-factor models. Journal of derivatives, 2(1), 7-16.