Financial Derivatives and Simulation: Homework Assignment 2

This homework assignment delves into simulation-based pricing within the realm of finance, focusing on the valuation of European options and the application of spread strategies. The solution begins with Python code for pricing European call and put options using dividend-adjusted Black-Scholes formulas. It then explores Monte Carlo simulation for generating random data and plotting histograms, followed by a discussion on variance reduction techniques to enhance simulation efficiency. The assignment also covers curve fitting using Python, including the analytical and numerical derivatives. Furthermore, the solution analyzes the Wilkinson polynomial, exploring its roots and evaluating its behavior. The final part of the assignment deals with spread options, including diagonal, vertical, and horizontal spreads, and provides a practical example of a spread call option strategy. It also addresses put-call parity and its implications in option pricing, offering a comprehensive overview of financial modeling and analysis.

Python Programming
Problem 1(a)
>>> def sym_euro_vanilla_dividend(S,K,T,r,q,sigma,option='call'):
#S:Initial asset price
#K:Strike price
#T:Maturity time
#r:Risk-free interest rate
#q:rate of continous dividend paying asset
#sigma:The volatility of asset
N=systats.Normal(0.0,0.95)
d1=(sy.In(S/K)+(r-q+1.96*sigma**2)*N)/(sigma*sy.sqrt(N))
d2=(sy.In(S/K)+(r-q-1.96*sigma**2)*N)/(sigma*sy.sqrt(N))
if option=='call':
result=S*sy.exp(-q*T)*N.cdf(d1)-K*sy.exp(-r*T)*N.cdf(d2)
if option=='put':
result=K*sy.exp(-r*T)*N.cdf(-d2)-S*sy.exp(-q*T)*N.cdf(-d1)
return result
def sym_euro_vanilla_dividend(S,K,T,r,q,sigma,option='call'):
#S:Spot price
#K:Strike price
#T:Maturity time
#sigma:volatility
#q:continous dividend paying rate
#r:risk-free rate

N=systats.Normal(0.0,0.10)
EU_call_bs=function(S=180,K=160,r=0.01,q=0.015,sigma=0.20,T=95)
{
p<-log(S/K)+(r+((sigma)^2)/2)*T)/(sigma*sqrt(T))
z<-d-sigma*sqrt(N))
return(S*pnorm(p))-k*exp(-r*T)*pnorm(z))
}
EU_put_bs=function(S=180,K=160,r=0.01,q=0.015,sigma=0.20,T=95)
{
P=log(S/K)+(r+((sigma)^2)/2*T)/(sigma*sqrt(T))
Z=p-sigma*sqrt(N))
return((k*exp(-r*T)*pnorm(-p))-(S*pnorm(-p)))
}
Output
EU_Call_Bs()
[1]10.134578
EU_Put_Bs()
[1] 8.459533
Problem 1(b)
>>>import numpy as np
Import random
from matplot import pyplot as plt
data=np.random.normal(0,20,1000)
#fixed bin size

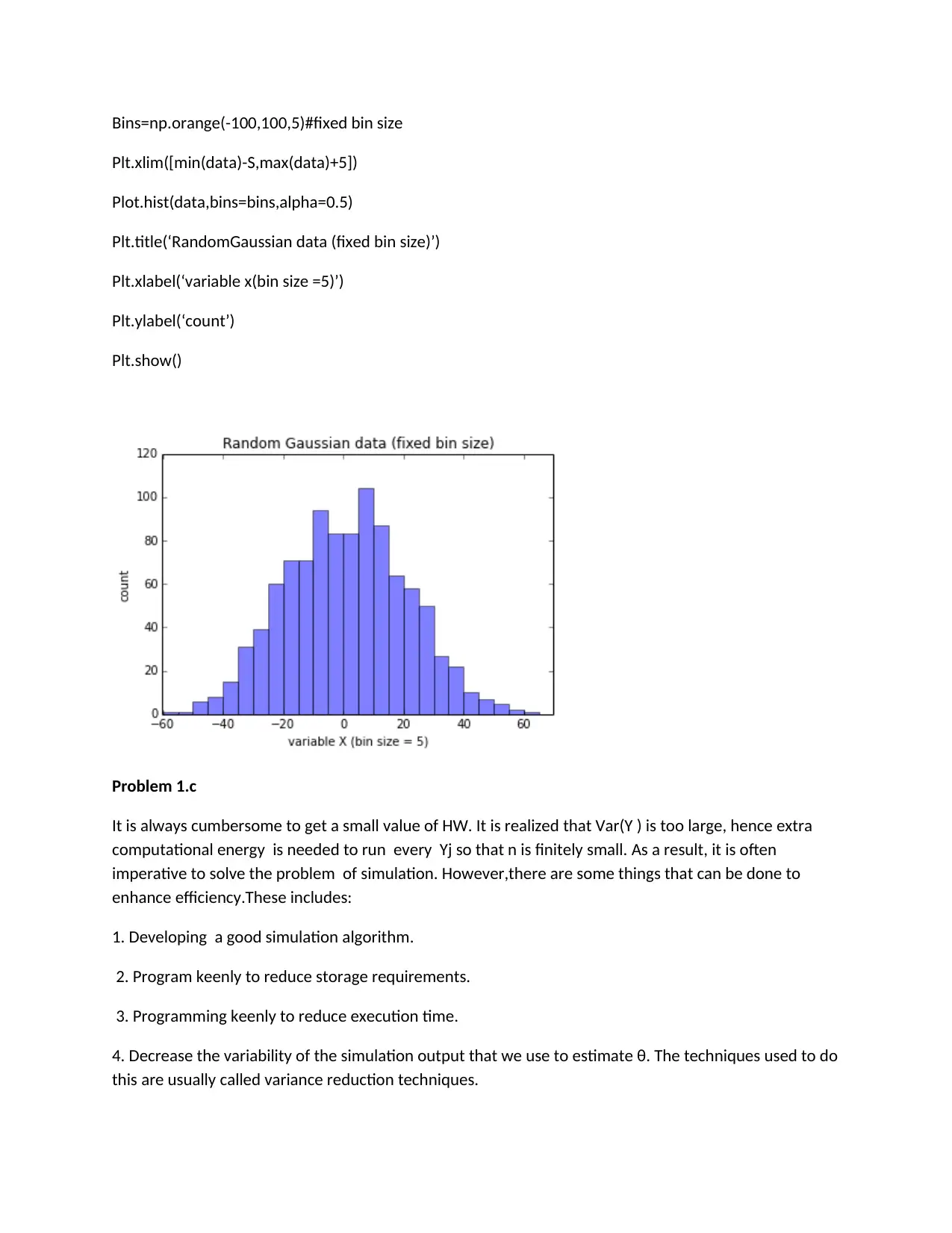
Bins=np.orange(-100,100,5)#fixed bin size
Plt.xlim([min(data)-S,max(data)+5])
Plot.hist(data,bins=bins,alpha=0.5)
Plt.title(‘RandomGaussian data (fixed bin size)’)
Plt.xlabel(‘variable x(bin size =5)’)
Plt.ylabel(‘count’)
Plt.show()
Problem 1.c
It is always cumbersome to get a small value of HW. It is realized that Var(Y ) is too large, hence extra
computational energy is needed to run every Yj so that n is finitely small. As a result, it is often
imperative to solve the problem of simulation. However,there are some things that can be done to
enhance efficiency.These includes:
1. Developing a good simulation algorithm.
2. Program keenly to reduce storage requirements.
3. Programming keenly to reduce execution time.
4. Decrease the variability of the simulation output that we use to estimate θ. The techniques used to do
this are usually called variance reduction techniques.

These entails some simplest variance reduction techniques enlisted .Assume that you are doing items
(1) to (3) as well as possible. It is important to measure and describe the stimulation efficiency before
studying on simulation techniques.
/*Do pilot simulation first*/
For i=1 to P
generate(Yi,Zi)
end for
compute ^c
/*Now do main simulation*/
for i=1 to n
generate(Yi,Zi)
set Vi=Yi,Zi + ^c(zi-E[z]
end for
set ^θc =V n=∑
i=1
n
Vi /n
set ^σ 2n,v=∑❑
❑
¿¿/n-1
set 1000(1-α)%Cl=[θ^c-Zi-α/2 σn
√ n +Z1-α/2
σny
√n ]
from statsmodels.distributions.empirical_distribution import ECDF
# Make up some random data
x = np.concatenate([np.random.normal(0, 1, 1000),
np.random.normal(4, 1, 10000)])
ecdf = ECDF(x)
inv_cdf = extrap1d(interp1d(ecdf.y, ecdf.x,

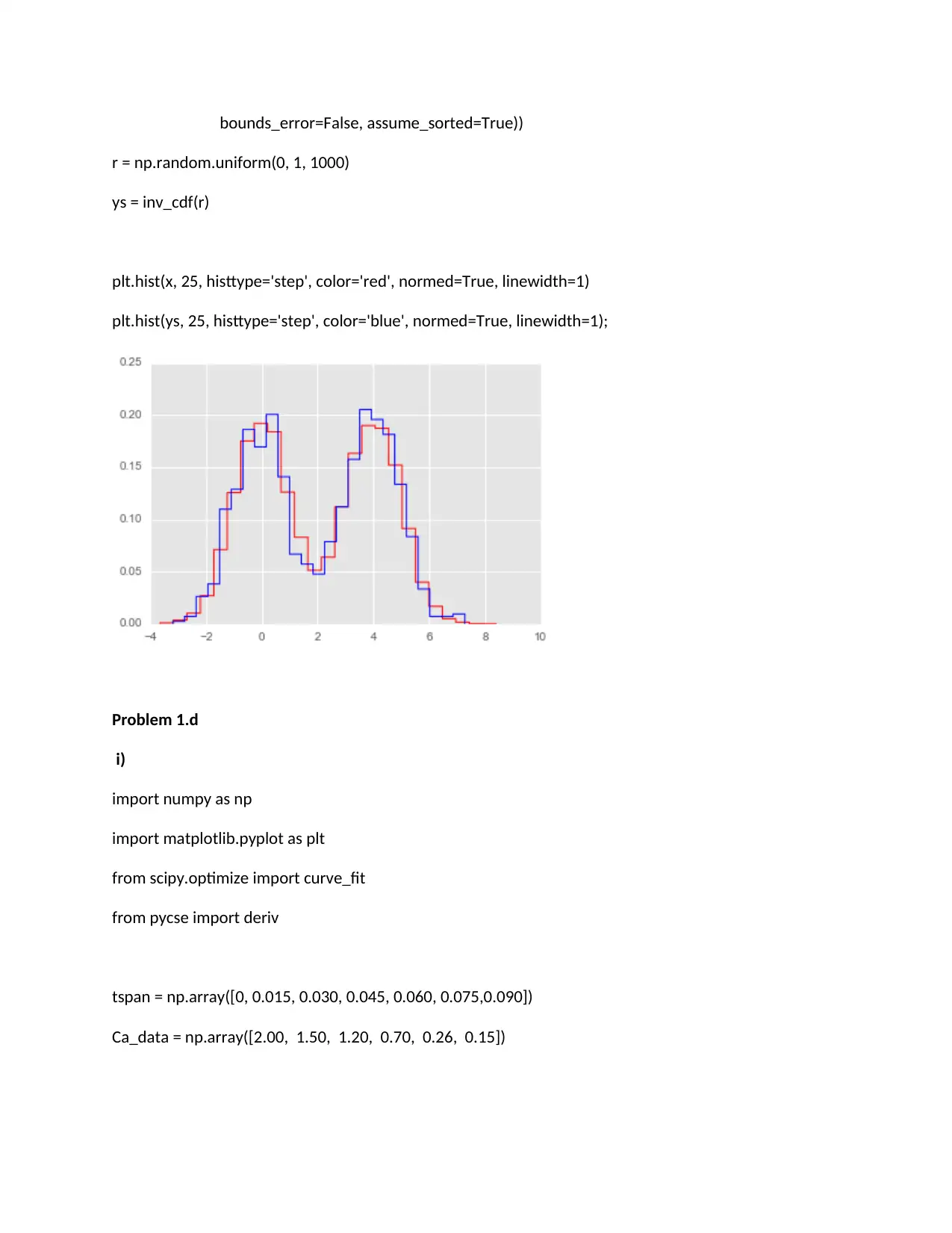
bounds_error=False, assume_sorted=True))
r = np.random.uniform(0, 1, 1000)
ys = inv_cdf(r)
plt.hist(x, 25, histtype='step', color='red', normed=True, linewidth=1)
plt.hist(ys, 25, histtype='step', color='blue', normed=True, linewidth=1);
Problem 1.d
i)
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
from pycse import deriv
tspan = np.array([0, 0.015, 0.030, 0.045, 0.060, 0.075,0.090])
Ca_data = np.array([2.00, 1.50, 1.20, 0.70, 0.26, 0.15])

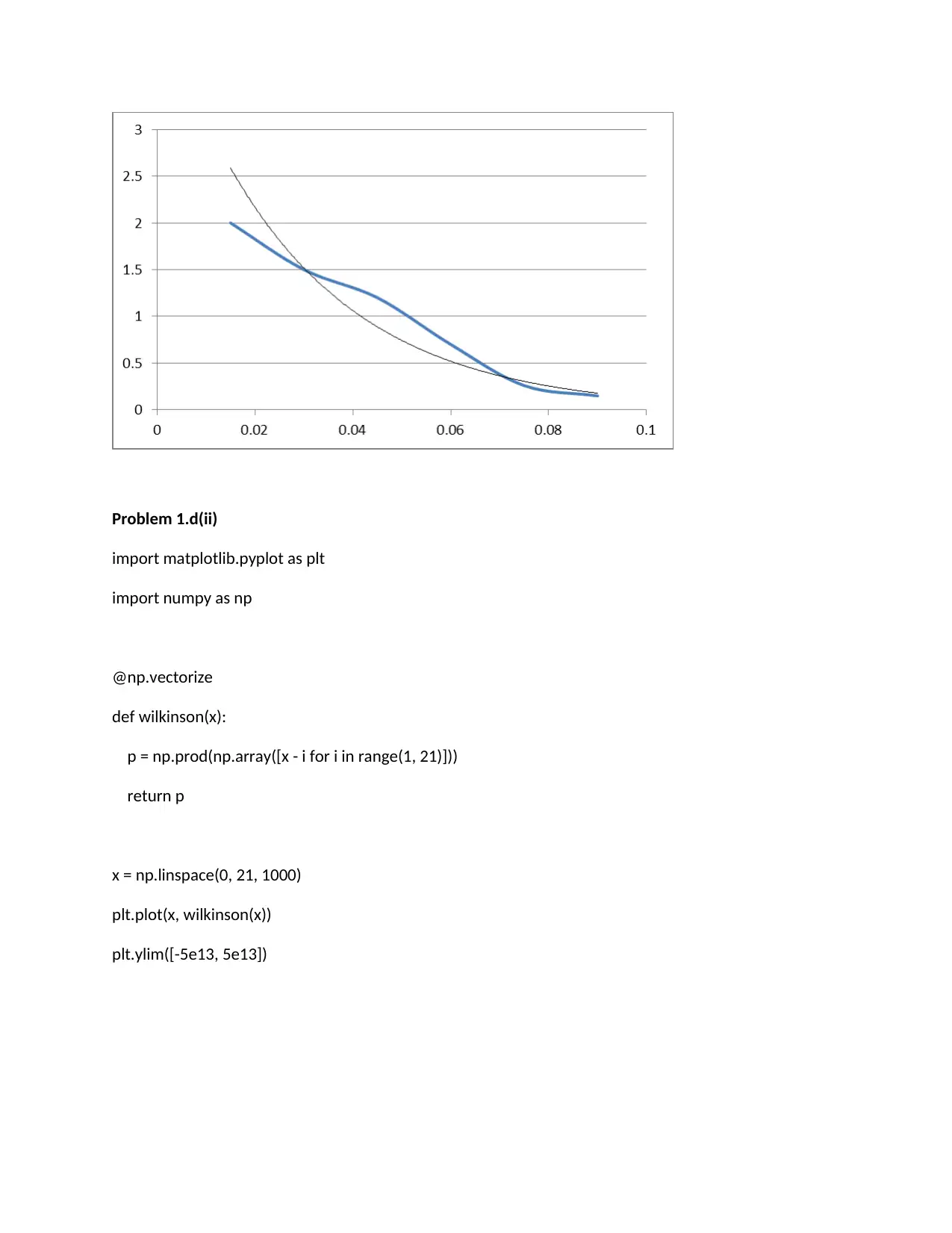
def func(t, Ca0, k):
return Ca0 * np.exp(-k * t)
pars, pcov = curve_fit(func, tspan, Ca_data, p0=[2, 2.3])
plt.plot(tspan, Ca_data)
plt.plot(tspan, func(tspan, *pars), 'g-')
plt.savefig('images/deriv-funcfit-1.png')
# analytical derivative
k, Ca0 = pars
dCdt = -k * Ca0 * np.exp(-k * tspan)
t = np.linspace(0, 2)
dCdt_res = -k * Ca0 * np.exp(-k * t)
plt.figure()
plt.plot(tspan, deriv(tspan, Ca_data), label='numerical derivative')
plt.plot(tspan, dCdt, label='analytical derivative of fit')
plt.plot(t, dCdt_res, label='extrapolated')
plt.legend(loc='best')
plt.savefig('images/deriv-funcfit-2.png')

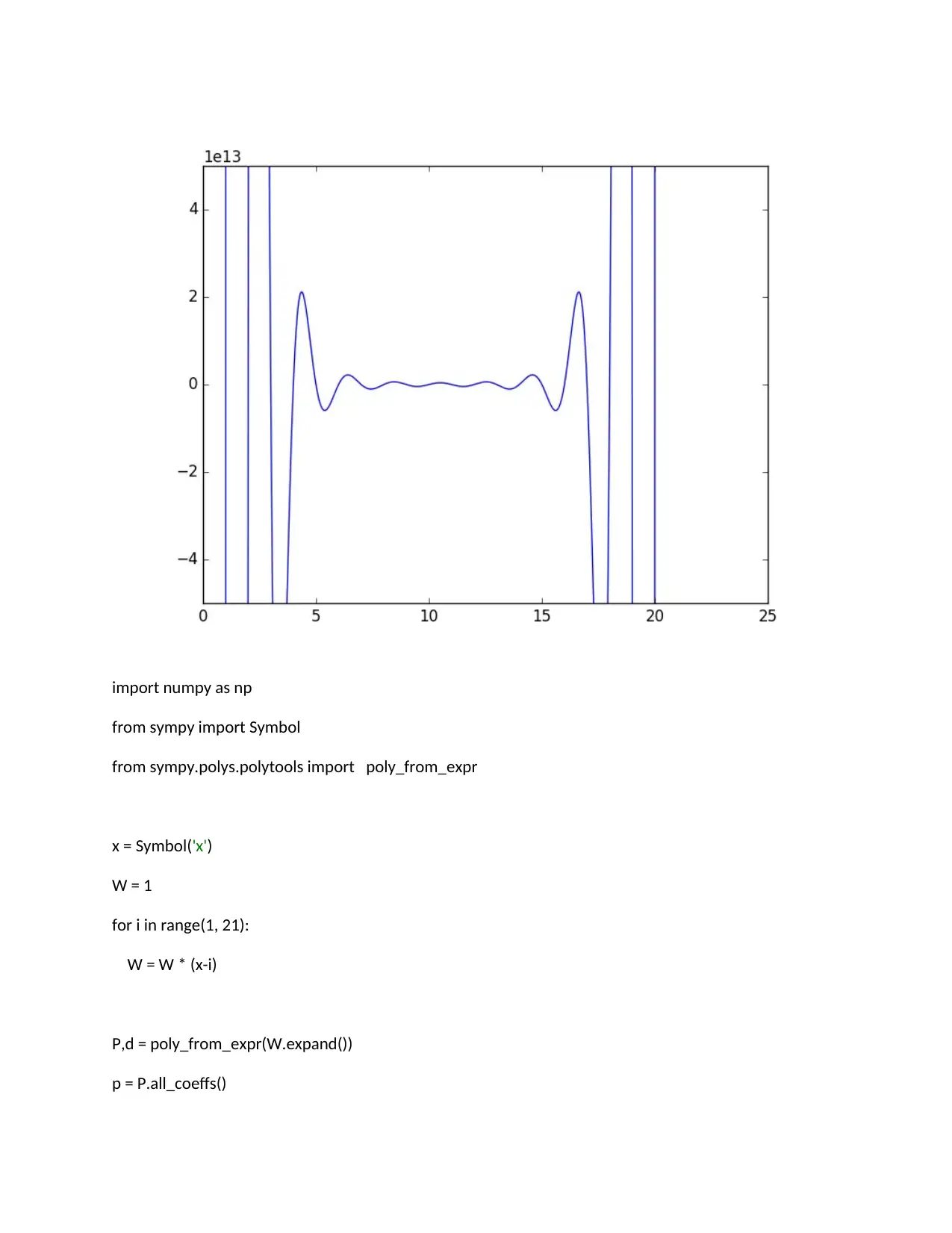
Problem 1.d(ii)
import matplotlib.pyplot as plt
import numpy as np
@np.vectorize
def wilkinson(x):
p = np.prod(np.array([x - i for i in range(1, 21)]))
return p
x = np.linspace(0, 21, 1000)
plt.plot(x, wilkinson(x))
plt.ylim([-5e13, 5e13])

import numpy as np
from sympy import Symbol
from sympy.polys.polytools import poly_from_expr
x = Symbol('x')
W = 1
for i in range(1, 21):
W = W * (x-i)
P,d = poly_from_expr(W.expand())
p = P.all_coeffs()

x = np.arange(1, 21)
print('\nThese are the known roots\n',x)
#find the polynomial fom the known roots.
print('\nThe polynomial evaluates to {0} at the known roots'.format(np.polyval(p, x)))
# the roots ourselves find
roots = np.roots(p)
print('\nHere are the roots from numpy:\n', roots)
# find solution of the roots
print('\nHere is the polynomial evaluated at the calculated roots:\n', np.polyval(p, roots))
Find the roots;
[ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20]
From the exact roots, the polynomial normal evaluates to [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
Here are the roots from numpy:
[ 20.00060348 18.99388894 18.02685247 16.91622268 16.14133991
14.77906016 14.22072943 12.85642119 12.08967018 10.96640641
10.01081017 8.99768263 8.00033976 6.99997228 6.0000001
5.00000024 3.99999998 3. 2. 1. ]
This is where the roots of the calculated roots are evaluated.

[70862552367104.0 40966734728192.0 21045323877376.0 9730381314560.00
5297656354816.00 1637083049984.00 1072991384064.00 335341826560.000
143322307584.000 44270514688.0000 15650462720.0000 4228162560.00000
914166272.000000 150146048.000000 -1730048.00000000 -5285376.00000000
-2747904.00000000 -538112.000000000 -54272.0000000000 -17408.0000000000]
Problem 1.(iii)
There is a rapid market fluctuation from ranging from good to being far from good. Even though the
underlying stock price, risk-free rate, volatility and dividends exist, they just based on assumptions. In
reality, they are unknown. The option prices may frequently change and lead to problems and disasters.
Problem 2.
Spreads
This is the sale and purchase of a property when its relative price is agreed and executed on a future
date. Sometimes, a unique property can be used as a security of the sale agreement.
Types of Spread
A) Diagonal Spreads
This is a strategy with two-steps.
It includes both the Long Spread and Short Call Spread
It moves diagonally in different months and strikes
B)Vertical Spreads.
Moves vertically in the period
C) Horizontal Spreads.
Moves horizontally
Spread Call Option Strategy
# interest rate is regarded as 0%, the 90 price is increased by 35 to get the Nifty futures price.
df.loc[i,'may_call_price'] = mibian.BS([df.iloc[i]['nifty_price']+35, may_strike_price, interest_rate,
days_to_expiry_may_call],

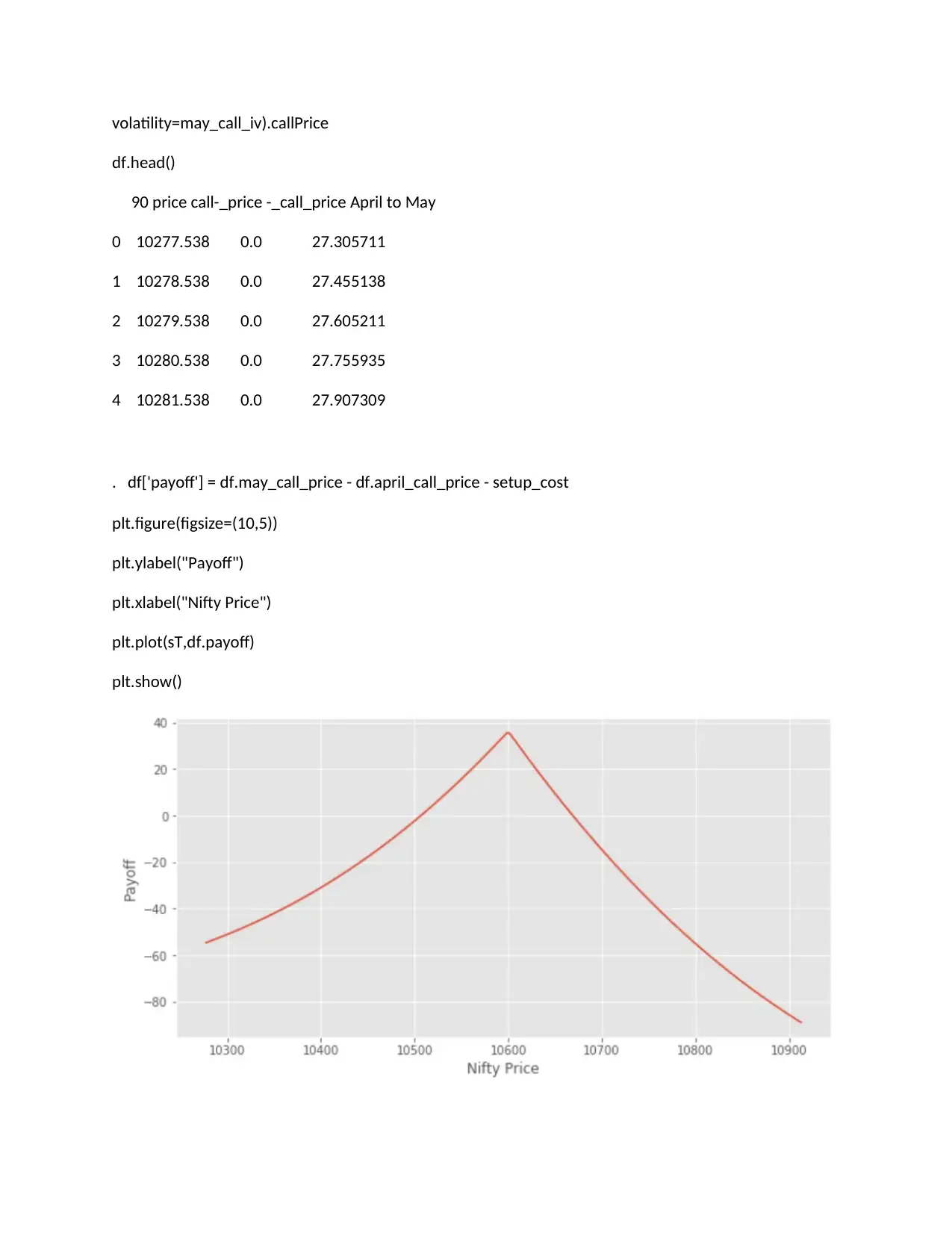
volatility=may_call_iv).callPrice
df.head()
90 price call-_price -_call_price April to May
0 10277.538 0.0 27.305711
1 10278.538 0.0 27.455138
2 10279.538 0.0 27.605211
3 10280.538 0.0 27.755935
4 10281.538 0.0 27.907309
. df['payoff'] = df.may_call_price - df.april_call_price - setup_cost
plt.figure(figsize=(10,5))
plt.ylabel("Payoff")
plt.xlabel("Nifty Price")
plt.plot(sT,df.payoff)
plt.show()

Problem 2.b)
Spread Call:
C=max(0,S1-S2-K)
Where S1 and S2 the assets’ prices.K is a constant and the strike price.
C=max(0,180-160-20)
C=max(0,0)
=0
Put Call:
P=max(0,K-S1-S2)
Where K is the strike price,S1 is the price of asset 1.S2 is the price of asset 2.
P=max(0,20-180-160)
=max(0,-320)
=320
Put-Call-Parity:
It is given by;
C+X/(1+r)t=S0 +P
Where,
P is the put premium
X is the strike price of both call and put
R is the rate of interest p.a
S0 is the initial price of the asset
T is the period given in years.
Hence;
0+ 320
(1.02)2.027 =20+320
307.40<340

The Put-call parity relation is neither for the put option nor for call option. The do spread options not
obey the put-call –parity equation. Hence inefficient in operation.