Maths Assignment: Financial Analysis, Equations and Calculations
VerifiedAdded on 2020/04/21
|11
|820
|106
Homework Assignment
AI Summary
This document presents a comprehensive solution to a finance-focused mathematics assignment. It begins by exploring market equilibrium, demand and supply functions, and calculating price elasticity of supply and consumer surplus. The assignment then delves into monopoly analysis, including total revenue, marginal revenue, profit maximization, and verifying the maximum profit using second-order conditions. Section B utilizes matrix algebra to solve systems of simultaneous equations, including finding determinants, cofactors, and inverses. The assignment also addresses financial concepts such as compound interest, calculating the annual equivalent rate (AER), net present value (NPV) analysis for investment decisions, loan calculations, and the maximum price for an annuity. The solutions provided demonstrate the application of mathematical principles to real-world financial scenarios.

Maths
Student Name:
Student Number:
Lecturer Name:
5th November 2017
Student Name:
Student Number:
Lecturer Name:
5th November 2017
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Section A:
1. The demand function in a competitive market is qD =22 – 0.2 p, while the supply is given
by qs=0.4 p – 8.
a) What is the inverse supply function?
Solution
0.4 p=qs+ 8
p= qs
0.4 + 8
0.4
p=2.5 qs +20
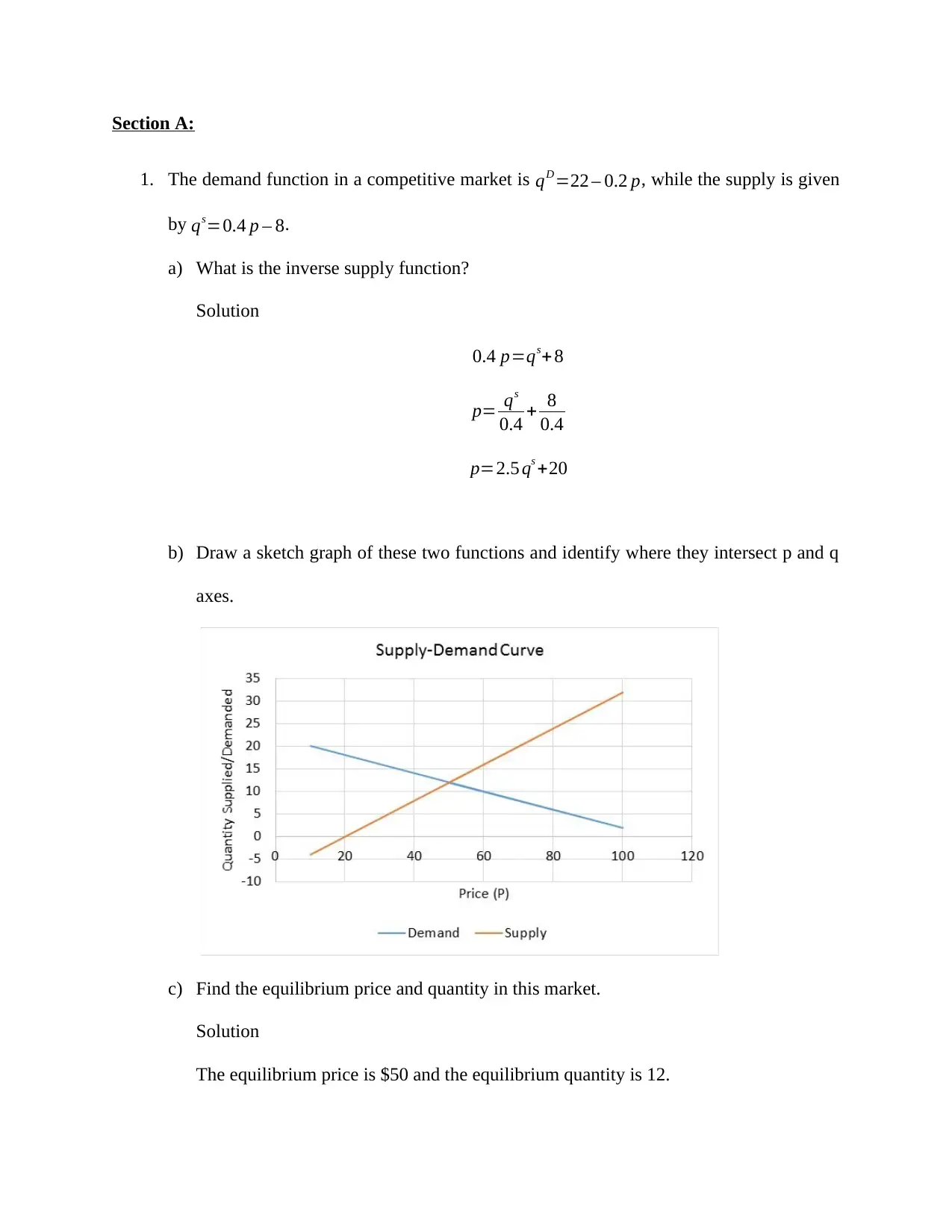
b) Draw a sketch graph of these two functions and identify where they intersect p and q
axes.
c) Find the equilibrium price and quantity in this market.
Solution
The equilibrium price is $50 and the equilibrium quantity is 12.
1. The demand function in a competitive market is qD =22 – 0.2 p, while the supply is given
by qs=0.4 p – 8.
a) What is the inverse supply function?
Solution
0.4 p=qs+ 8
p= qs
0.4 + 8
0.4
p=2.5 qs +20
b) Draw a sketch graph of these two functions and identify where they intersect p and q
axes.
c) Find the equilibrium price and quantity in this market.
Solution
The equilibrium price is $50 and the equilibrium quantity is 12.

d) Calculate the price elasticity of supply when quantity is 15. Interpret your result.
Solution
For supply we have: p=2.5Q+20
For demand we have: p=−5Q+110
From above ∆ Q
∆ P = 2.5; the gradient of p=2.5Q+20
The associated price when quantity is 15 is;
P=2.5*15+20=57.5
Point Price Elasticity of Quantity = (% change in Quantity)/(% change in Price)
Point Price Elasticity of Quantity = ( ∆ Q
Q ) / ( ∆ P
P )
Point Price Elasticity of Quantity = ( P
Q )( ∆ Q
∆ P )
Elasticity = 2.5 *(57.5/15) = 9.58
As can be seen, the elasticity is greater than 1; this means that a given percentage
change in price leads to a larger change in quantity supplied.
e) Calculate the consumer surplus at the equilibrium point.
Solution
Solution
For supply we have: p=2.5Q+20
For demand we have: p=−5Q+110
From above ∆ Q
∆ P = 2.5; the gradient of p=2.5Q+20
The associated price when quantity is 15 is;
P=2.5*15+20=57.5
Point Price Elasticity of Quantity = (% change in Quantity)/(% change in Price)
Point Price Elasticity of Quantity = ( ∆ Q
Q ) / ( ∆ P
P )
Point Price Elasticity of Quantity = ( P
Q )( ∆ Q
∆ P )
Elasticity = 2.5 *(57.5/15) = 9.58
As can be seen, the elasticity is greater than 1; this means that a given percentage
change in price leads to a larger change in quantity supplied.
e) Calculate the consumer surplus at the equilibrium point.
Solution
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
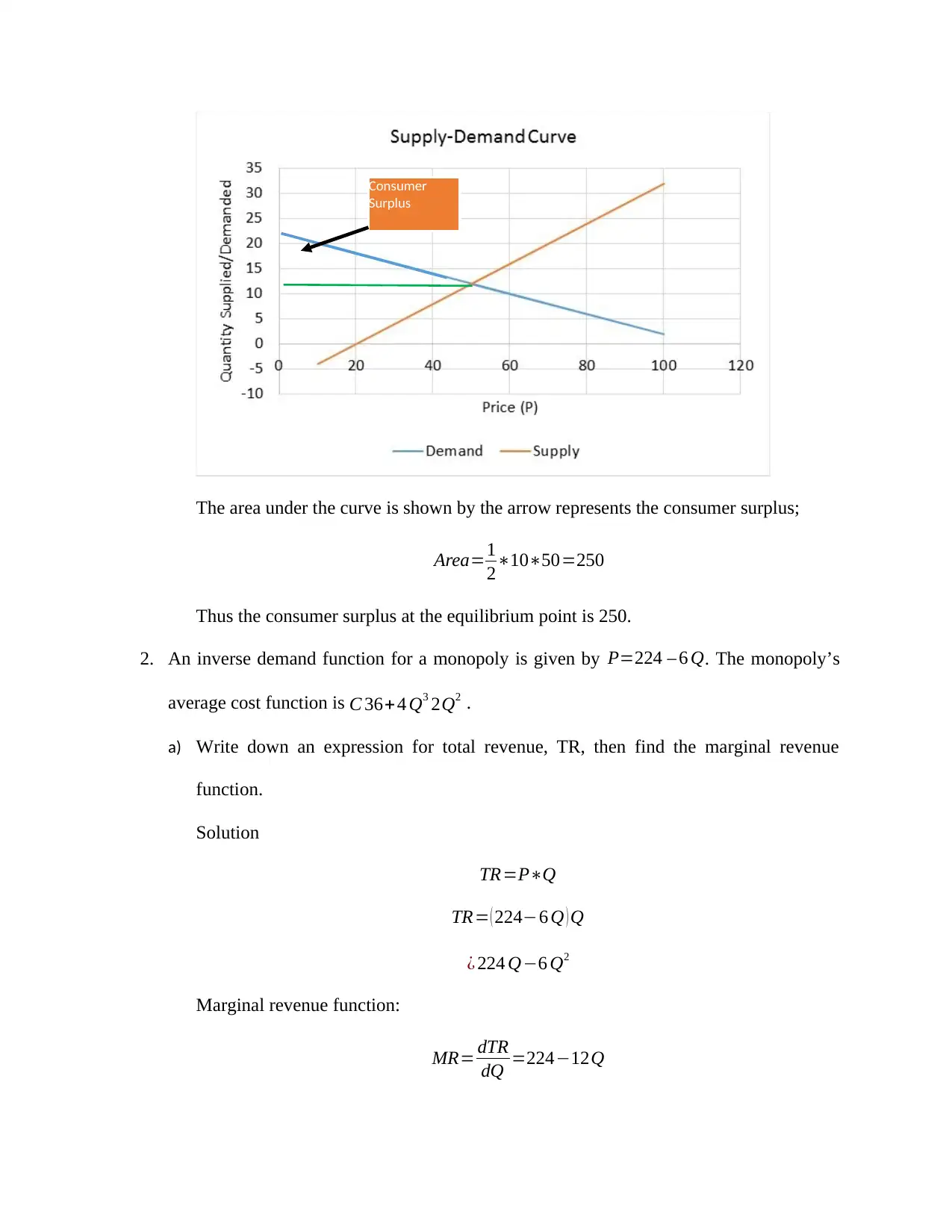
The area under the curve is shown by the arrow represents the consumer surplus;
Area=1
2∗10∗50=250
Thus the consumer surplus at the equilibrium point is 250.
2. An inverse demand function for a monopoly is given by P=224 – 6 Q. The monopoly’s
average cost function is C 36+4 Q3 2Q2 .
a) Write down an expression for total revenue, TR, then find the marginal revenue
function.
Solution
TR=P∗Q
TR= ( 224−6 Q ) Q
¿ 224 Q−6 Q2
Marginal revenue function:
MR= dTR
dQ =224−12Q
Consumer
Surplus
Area=1
2∗10∗50=250
Thus the consumer surplus at the equilibrium point is 250.
2. An inverse demand function for a monopoly is given by P=224 – 6 Q. The monopoly’s
average cost function is C 36+4 Q3 2Q2 .
a) Write down an expression for total revenue, TR, then find the marginal revenue
function.
Solution
TR=P∗Q
TR= ( 224−6 Q ) Q
¿ 224 Q−6 Q2
Marginal revenue function:
MR= dTR
dQ =224−12Q
Consumer
Surplus
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

b) Write down an expression for the monopoly’s profit, π.
Solution
π=P−TC
¿ ( 224−6 Q )−(36+ 4 Q3 2Q2 )
¿ 224−6 Q−36−4 Q3 +2Q2
¿ 188−6 Q−4 Q3+2Q2
c) Find the value of Q that maximizes the firm’s profit.
Solution
Max Profit:
MC= dTC
dQ =12Q2−4 Q
Using MC=MR
12 Q2−4 Q=224−12Q
12 Q2+ 8Q−224
3 Q2 +2Q−56=0
Solving yields;
Q=4
d) Use the second order condition to verify that the answer to part (c) represents a
maximum.
Solution
dπ
dQ =−6−12Q2 + 4 Q=0
12 Q2−4 Q+ 6=0
6 Q2−2 Q+3=0
Solution
π=P−TC
¿ ( 224−6 Q )−(36+ 4 Q3 2Q2 )
¿ 224−6 Q−36−4 Q3 +2Q2
¿ 188−6 Q−4 Q3+2Q2
c) Find the value of Q that maximizes the firm’s profit.
Solution
Max Profit:
MC= dTC
dQ =12Q2−4 Q
Using MC=MR
12 Q2−4 Q=224−12Q
12 Q2+ 8Q−224
3 Q2 +2Q−56=0
Solving yields;
Q=4
d) Use the second order condition to verify that the answer to part (c) represents a
maximum.
Solution
dπ
dQ =−6−12Q2 + 4 Q=0
12 Q2−4 Q+ 6=0
6 Q2−2 Q+3=0

d2 π
d Q2 =12 Q−2=0
e) Calculate the maximum value of profits that can be achieved by this monopoly. Is the
firm profitable?
Solution
π=188−6 Q−4 Q3 +2Q2
π=188−6∗4−4 ¿ ( 4 ) 3 +2∗( 4 ) 2
π=−$ 60
Yes the firm is not profitable.
Section B:
3. Use matrix algebra to solve the following system of equations:
x + y + z = 6
2y + 5z = -4
2x + 5y – z = 27
a) Write the above system of simultaneous equations in a matrix form.
Solution
[1 1 1
0 2 5
2 5 −1 ][ x
y
z ]=
[ 6
−4
27 ]
b) Find the determinant of matrix A.
Solution
A being a 3X3 matrix that is similar to;
For a 3×3 matrix (3 rows and 3 columns):
d Q2 =12 Q−2=0
e) Calculate the maximum value of profits that can be achieved by this monopoly. Is the
firm profitable?
Solution
π=188−6 Q−4 Q3 +2Q2
π=188−6∗4−4 ¿ ( 4 ) 3 +2∗( 4 ) 2
π=−$ 60
Yes the firm is not profitable.
Section B:
3. Use matrix algebra to solve the following system of equations:
x + y + z = 6
2y + 5z = -4
2x + 5y – z = 27
a) Write the above system of simultaneous equations in a matrix form.
Solution
[1 1 1
0 2 5
2 5 −1 ][ x
y
z ]=
[ 6
−4
27 ]
b) Find the determinant of matrix A.
Solution
A being a 3X3 matrix that is similar to;
For a 3×3 matrix (3 rows and 3 columns):
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

The determinant is:
¿ A∨¿ a( ei−fh)−b(di−fg)+c (dh−eg)
|A|=1 (−2−25 )−1 ( 0−10 ) +1 ( 0−4 )=−27+ 10−4=−21
c) Find the matrix of cofactors of matrix A.
Solution
A11=|2 5
5 −1|=−27 A12=−|0 5
2 −1|=10 A13=|0 2
2 5|=−4
A21=−|1 1
5 −1|=6 A22=|1 1
2 −1|=−3 A23=−|1 1
2 5|=−3
A31=|1 1
2 5|=3 A32=−|1 1
0 5|=−5 A33=|1 1
0 2|=2
The cofactor matrix is thus [−27 10 −4
6 −3 −3
3 −5 2 ]
d) Find the inverse of A, i.e. A-1.
Solution
A−1=−1
21 adj ( A )=−1
21 [−27 6 3
10 −3 −5
−4 −3 2 ]=
[ 9/7 −2/7 −1/ 7
−10/21 1/7 5 /21
4 / 21 1/7 −2 /21 ]
e) Using your answer to part (d), find the solution to the above system of simultaneous
equations.
Solution
¿ A∨¿ a( ei−fh)−b(di−fg)+c (dh−eg)
|A|=1 (−2−25 )−1 ( 0−10 ) +1 ( 0−4 )=−27+ 10−4=−21
c) Find the matrix of cofactors of matrix A.
Solution
A11=|2 5
5 −1|=−27 A12=−|0 5
2 −1|=10 A13=|0 2
2 5|=−4
A21=−|1 1
5 −1|=6 A22=|1 1
2 −1|=−3 A23=−|1 1
2 5|=−3
A31=|1 1
2 5|=3 A32=−|1 1
0 5|=−5 A33=|1 1
0 2|=2
The cofactor matrix is thus [−27 10 −4
6 −3 −3
3 −5 2 ]
d) Find the inverse of A, i.e. A-1.
Solution
A−1=−1
21 adj ( A )=−1
21 [−27 6 3
10 −3 −5
−4 −3 2 ]=
[ 9/7 −2/7 −1/ 7
−10/21 1/7 5 /21
4 / 21 1/7 −2 /21 ]
e) Using your answer to part (d), find the solution to the above system of simultaneous
equations.
Solution
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Multiply both sides of the matrix equations with the inverse;
[ 9/7 −2 /7 −1/7
−10/ 21 1/7 5/21
4 /21 1/7 −2/21 ][1 1 1
0 2 5
2 5 −1 ][ x
y
z ]= [ 9/7 −2 /7 −1/7
−10/21 1/7 5/21
4 /21 1/7 −2/21 ][ 6
−4
27 ]
[1 0 0
0 1 0
0 0 1 ][ x
y
z ]= [ 5
3
−2 ]
4. Answer the following questions:
a) If a saving account pays 4.5% nominal interest, how long would any given sum of
money take to quadruple its value? Assume monthly compounding.
Solution
A=p (1+ r
n )nt
4 p= p ( 1+ 0.045
12 )
12 t
4= (1+ 0.045
12 )12 t
4= (1.00375 )12t
12 t log 1.00375=log 4
12 t∗0.001626=0.60206
t= 0.60206
12∗0.001626 =30.86427
It will take about 30.86 years
b) If £2,000 is to accumulate to £2,125 after being invested for 5 months, what is the
corresponding AER? Assume monthly compounding.
Solution
[ 9/7 −2 /7 −1/7
−10/ 21 1/7 5/21
4 /21 1/7 −2/21 ][1 1 1
0 2 5
2 5 −1 ][ x
y
z ]= [ 9/7 −2 /7 −1/7
−10/21 1/7 5/21
4 /21 1/7 −2/21 ][ 6
−4
27 ]
[1 0 0
0 1 0
0 0 1 ][ x
y
z ]= [ 5
3
−2 ]
4. Answer the following questions:
a) If a saving account pays 4.5% nominal interest, how long would any given sum of
money take to quadruple its value? Assume monthly compounding.
Solution
A=p (1+ r
n )nt
4 p= p ( 1+ 0.045
12 )
12 t
4= (1+ 0.045
12 )12 t
4= (1.00375 )12t
12 t log 1.00375=log 4
12 t∗0.001626=0.60206
t= 0.60206
12∗0.001626 =30.86427
It will take about 30.86 years
b) If £2,000 is to accumulate to £2,125 after being invested for 5 months, what is the
corresponding AER? Assume monthly compounding.
Solution

A=p ( 1+ r
n )
nt
2125=2000 ( 1+ r
12 )
5
1.0625= ( 1+ r
12 )
5
From the above, we obtain the rate to be 14.638%
The AER that corresponds to a rate r added n times per year is given by AER ( 1+r ) n −1
AER= ( 1+r ) n−1
¿ ( 1+0.14638 ) 5 /12−1=0.058572
AER=5.8572 %
c) Assuming that the relevant interest rate is at 6%, use the NPV method to advise an
investor whether to commit to a project associated with the following money flows:
Year Project A
Initial Outlay £ 120,000
Return at end of year 1 £ 20,000
Return at end of year 2 £ 40,000
Return at end of year 3 £ 0
Return at end of year 4 £ 80,000
Year One: 20000
(1+0.06)1 =$ 18,867.92
Year Two: 40000
(1+0.06)2 =$ 35,599.86
Year Three: 0
(1+0.06)3 =$ 0
Year Four: 80000
(1+0.06)4 =$ 63,367.49
n )
nt
2125=2000 ( 1+ r
12 )
5
1.0625= ( 1+ r
12 )
5
From the above, we obtain the rate to be 14.638%
The AER that corresponds to a rate r added n times per year is given by AER ( 1+r ) n −1
AER= ( 1+r ) n−1
¿ ( 1+0.14638 ) 5 /12−1=0.058572
AER=5.8572 %
c) Assuming that the relevant interest rate is at 6%, use the NPV method to advise an
investor whether to commit to a project associated with the following money flows:
Year Project A
Initial Outlay £ 120,000
Return at end of year 1 £ 20,000
Return at end of year 2 £ 40,000
Return at end of year 3 £ 0
Return at end of year 4 £ 80,000
Year One: 20000
(1+0.06)1 =$ 18,867.92
Year Two: 40000
(1+0.06)2 =$ 35,599.86
Year Three: 0
(1+0.06)3 =$ 0
Year Four: 80000
(1+0.06)4 =$ 63,367.49
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

NPV=
( $ 18,867.92+ $ 35,599.86+ $ 0+ $ 63,367.49 ) −$ 120,000=$ 117,835.3−$ 120,000=−$ 2,164.72
The NPV is negative the investor should therefore not commit to a project associated
with the above money flows.
d) You wish to buy a car priced at £12,000 by putting down a cash deposit of £1,500 and
borrowing the remaining amount. The loan will be paid back in monthly instalments
over 4 years. How much will you have to budget to pay each month if the
corresponding APR is 6.8%?
Solution
Amount borrowed £12,000 - £1,500 =£10,500
P=R
[ 1− (1+ r
n )−nt
r
n ]
R=P
[ 1− ( 1+ r
n )
nt
r
n ]
R= 10,500
[ 1− (1+ 0.068
12 )− 48
0.068
12 ]=£ 250.4624
The monthly budget is £ 250.4624
e) What is a maximum price an investor should pay for an annuity that promises to
make payments of £4,000 a year, commencing in 12 months’ time, for the next 15
( $ 18,867.92+ $ 35,599.86+ $ 0+ $ 63,367.49 ) −$ 120,000=$ 117,835.3−$ 120,000=−$ 2,164.72
The NPV is negative the investor should therefore not commit to a project associated
with the above money flows.
d) You wish to buy a car priced at £12,000 by putting down a cash deposit of £1,500 and
borrowing the remaining amount. The loan will be paid back in monthly instalments
over 4 years. How much will you have to budget to pay each month if the
corresponding APR is 6.8%?
Solution
Amount borrowed £12,000 - £1,500 =£10,500
P=R
[ 1− (1+ r
n )−nt
r
n ]
R=P
[ 1− ( 1+ r
n )
nt
r
n ]
R= 10,500
[ 1− (1+ 0.068
12 )− 48
0.068
12 ]=£ 250.4624
The monthly budget is £ 250.4624
e) What is a maximum price an investor should pay for an annuity that promises to
make payments of £4,000 a year, commencing in 12 months’ time, for the next 15
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

years. Assume that money can be invested elsewhere at a nominal annual rate of
3.2%.
Solution
P=4000 [ 1− ( 1+0.032 )−15
0.032 ] =£ 47,068.23
Maximum price should be £ 47,068.23.
3.2%.
Solution
P=4000 [ 1− ( 1+0.032 )−15
0.032 ] =£ 47,068.23
Maximum price should be £ 47,068.23.
1 out of 11
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.



