CS 330: Language Theory, Finite Automata, and Grammar Homework

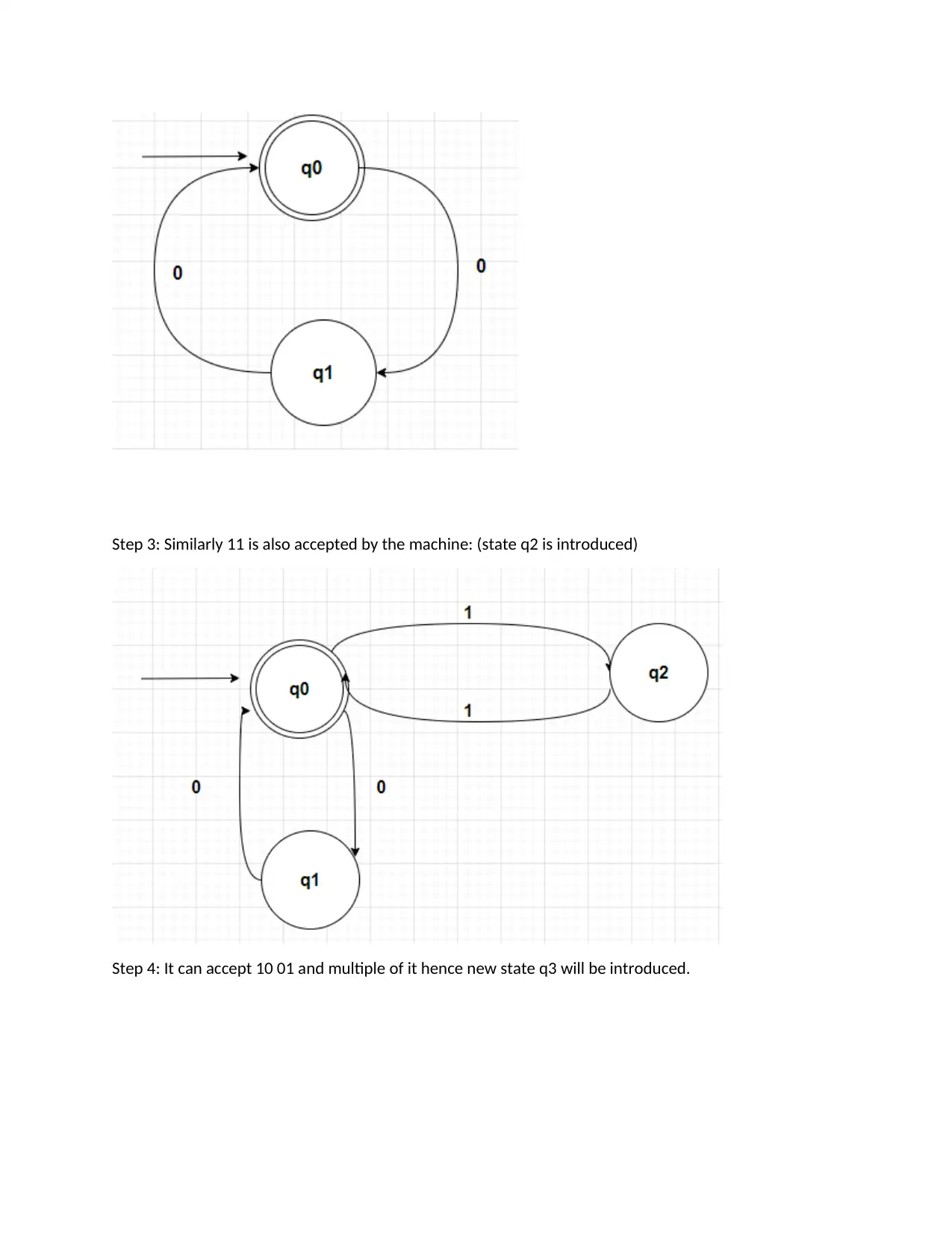
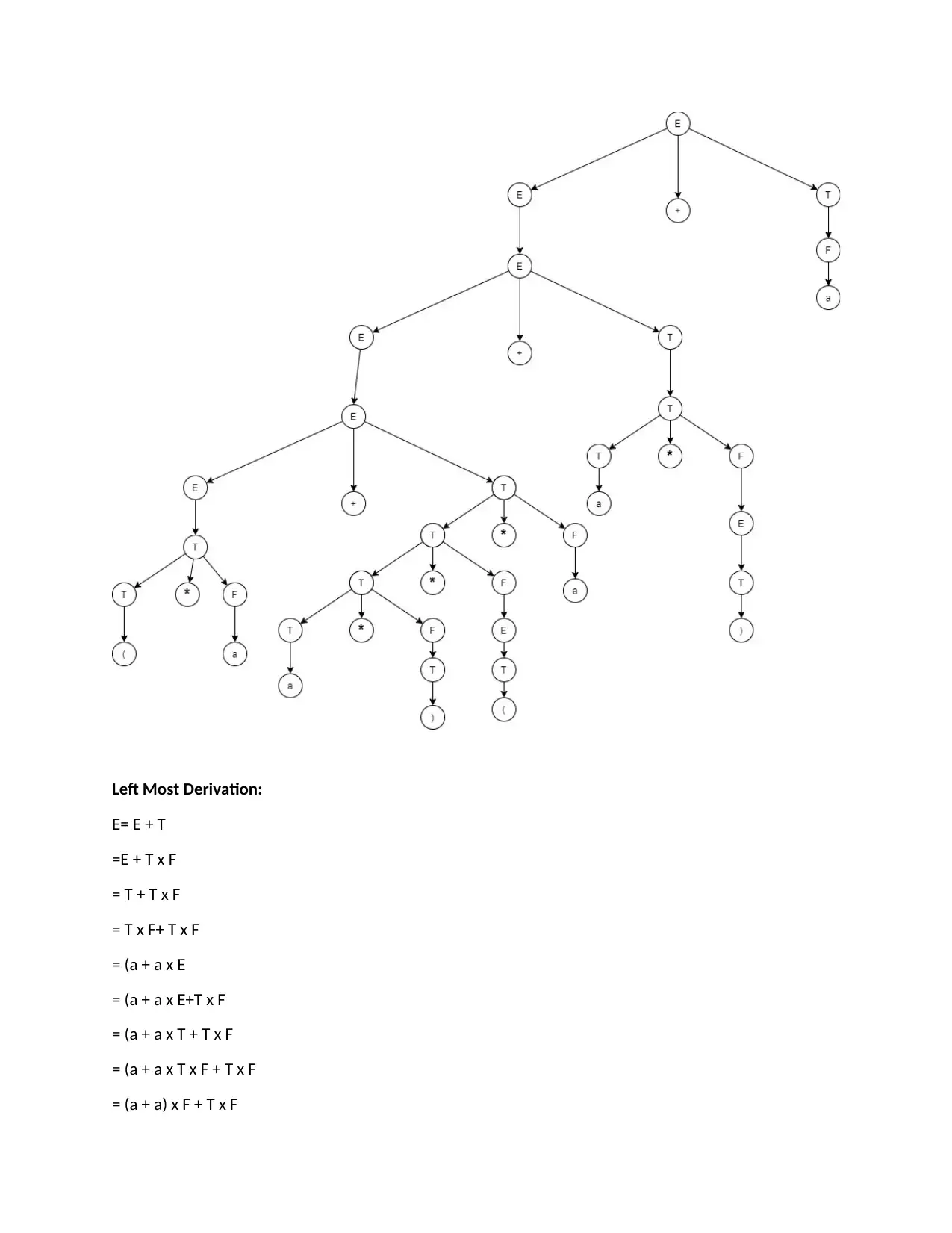
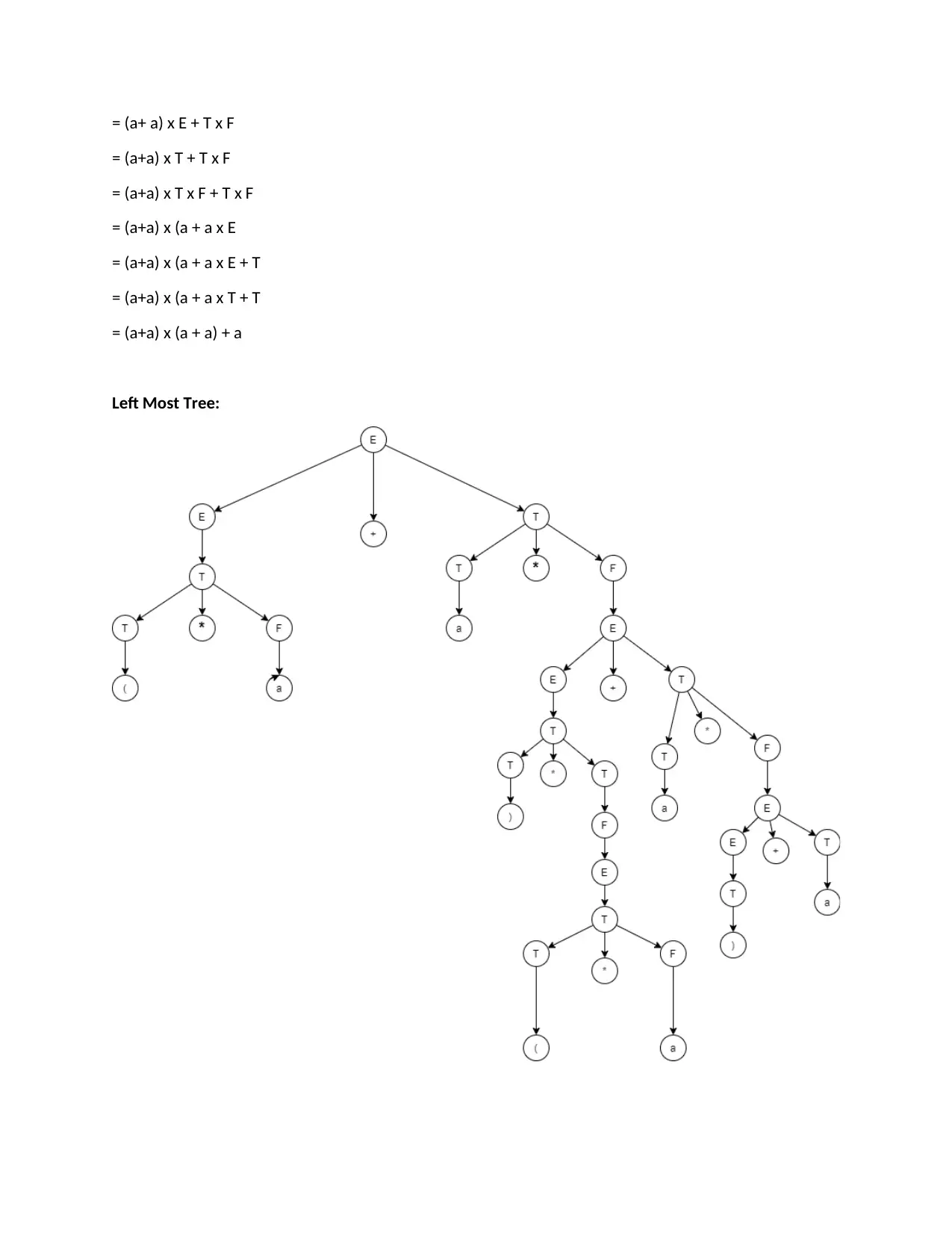
This document presents a comprehensive solution to a Language Theory and Finite Automata homework assignment. The solution begins by proving the closure of regular languages under the difference operation using the properties of Deterministic Finite Automata (DFA). It then provides a step-by-step conversion of a given regular expression into a Finite Automaton. The assignment also utilizes the Pumping Lemma to demonstrate that specific languages, namely {www | w is {a,b}*} and {0m1n0m | m, n >= 0}, are not regular. Furthermore, the solution includes the derivation of the expression (a + a) × (a + a) + a, using both leftmost and rightmost derivations, accompanied by the respective derivation trees. Finally, it analyzes and compares the two derivation methods and their corresponding trees, highlighting their similarities and differences in terms of structure and complexity. This resource is designed to aid students in understanding and solving similar problems in language theory and automata.

Question 1: L1 – L2 is regular.
Proof: We here knows that L1-L2= L1∩L2
Given in the question that L1 and L2 are regular.
Consider, for regular expression L1, AL1 is the DFA and for regular expression L2, AL2 is the DFA
respectively.
This follows,
AL1 = (Q, Σ, δ, q0, F) is represented by L1.
And, AL2 = (Q, Σ, δ, q0, Q − F) is represented by L1.
We know that under union and complement regular languages are closed it implies that L 1U L 2= L1 ∩
L2 is a regular language.
Question 2: Convert Regular Expression to Finite
Automata:
Here provided regular expression is:
RE = (00 + 11 + (01 + 10)(00 + 11)*(01 + 10))*
The above Regular Expression is of EVEN- EVEN Language Regular expression.
It can accepts only even number of 0’s and 1’s: 00, 11, 0101, 1100, 0011, 1010, 100001..
Step 1 – If no 0 and 1 is present (empty) then also it is accepted, hence the first state is q0 :
Step 2: Based on the above example provided it can also accept 00: (state q1 is introduced)

Step 3: Similarly 11 is also accepted by the machine: (state q2 is introduced)
Step 4: It can accept 10 01 and multiple of it hence new state q3 will be introduced.

Hence the above figure is the finite automata for the given Regular expression - (00 + 11 + (01 + 10)(00 +
11)*(01 + 10))*.
Question 3:
a. {www | w is {a,b}*}
Here to prove that provided expression is not regular, we use the proof of contradiction. We will assume
the language provided is regular.
Let the L = {www | w is {a,b}*} and also L is regular. Hence L is regular than there is a pumping length
exists for it “p” (such that string s ∈ L when |s| ≥ p). Below are the conditions which s=xyz need to
follow:
Let’s consider string s= apbbapb, as it is Regular expression hence all the above conditions are fulfilled in
it:
As per the 1st condition, it is concluded that y=0k for value of k>0, and as per 2nd condition it can be
concluded that s is composed of x and y and as per condition 3 it can take any value of i. Let’s take i=2
and resulting string will be in expression L.
Hence xy2z should be in L and xy2z = xyyz = a(p+k)bbapb.

But we can see that above string cannot be split into www to be in L as required.
This implies, xy2z ∉ L. Hence the provide language is not regular, L= {www | w is {a,b}*}
b. {0m1n0m | m, n >= 0}
Again, here to prove that provided expression is not regular, we will utilize proof of contradiction. We
will assume provided language is regular.
Let the L = {0m1n0m | m, n >= 0}, and L is regular. Hence L is regular than there is a pumping length exists
for it “p” (such that string s ∈ L when |s| ≥ p). Below are the conditions which s=xyz need to follow:
Let’s consider string s= 0p10p, As it is Regular expression hence all the above conditions are fulfilled in it:
As per 1st condition, it follows that y=0k for value of k>0, and as per 2nd condition it follows that s is
composed of x and y and as per 3rd condition it can accept value of i=0 and resulting string will be in L.
Hence xy0z should be in L and xy0z = xz = 0(p−k)10p.
But we can see that above string is not in L and it is contradiction with Pumping lemma hence
{0m1n0m | m, n >= 0} is not Regular.
Question 4:
EXPR  EXPR + TERM | TERM
TERM  TERM × FACTOR | FACTOR
FACTOR  ( EXPR ) | a
(a + a) × (a + a) + a
Right most derivation:
E = EXPR
F = FACTOR

T = TERM
E= E + T
= E + F
= E + a
= E + T + a
= E + T + a
= E + T X F + a
= E + T x E + a
= E + T x T +a
= E + T x ) + a
= E + a) + a
= E + T + a ) + a
= E + T x F + a)+a
= E + T x a + a) + a
= E + T x F x a + a) +a
= E + T x E x a + a) + a
=E + T x E x a + a) +a
=E + T x T x a + a) + a
=E + T x (a+a) +a
= E + T x F x (a+a) +a
= E + T x T x (a+a) + a
= E + T ) x (a+a) +a
= E + a) x (a+a) + a
= T x F + a) x (a + a) + a
= (a + a) x (a+a) + a
Right Most Tree:

Left Most Derivation:
E= E + T
=E + T x F
= T + T x F
= T x F+ T x F
= (a + a x E
= (a + a x E+T x F
= (a + a x T + T x F
= (a + a x T x F + T x F
= (a + a) x F + T x F

= (a+ a) x E + T x F
= (a+a) x T + T x F
= (a+a) x T x F + T x F
= (a+a) x (a + a x E
= (a+a) x (a + a x E + T
= (a+a) x (a + a x T + T
= (a+a) x (a + a) + a
Left Most Tree:

The two derivation (left most and right most) variance in the order in which they replace the variable
but overall structure is similar and result is similar. Both the derivations indicates unambiguous grammar
and no possibility to of other derivation of it.
The two derivation tree are similar in the result but varies in the length, the left most tree is smaller in
length as compared to Right most. The Right most tree is bit complex as compared to left most. The left
most tree specifies the result in similar and efficient manner.