Finite Automata Solution

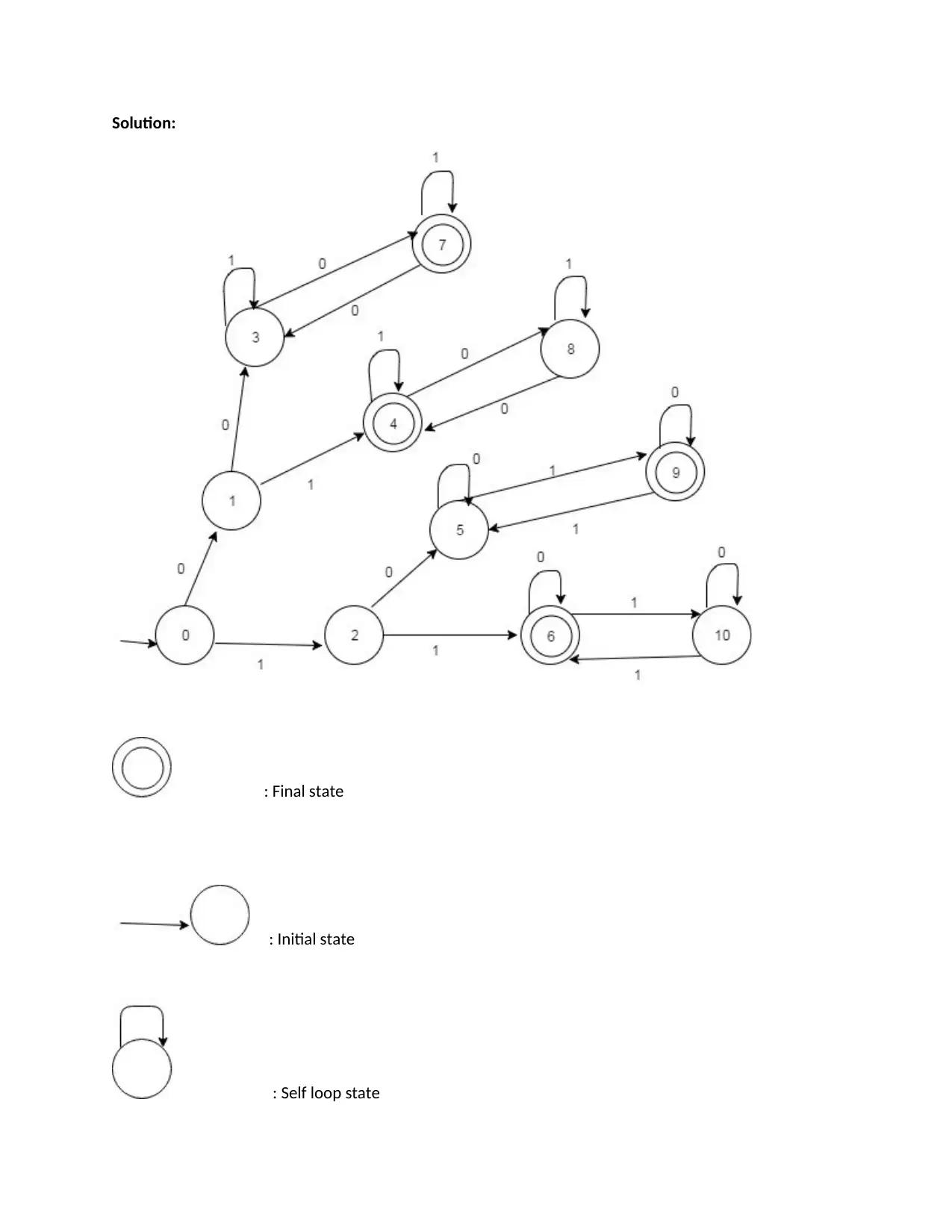
This document presents a solved practical assignment focusing on finite automata. The solution details the design and operation of a finite state machine that handles message encoding based on parity. Two test cases are included, demonstrating how the machine transitions between states based on input bits and parity checks. The solution explains the state transitions, parity calculations, and the final encoded message for each case. The assignment showcases a practical application of automata theory in data processing and encoding.

Solution:
: Final state
: Initial state
: Self loop state

STATE 0 TRANSITION 1 TRANSITION ACCEPTING
0 1 2 
1 3 4 
2 5 6 
3 7 3 
4 8 4 
5 5 9 
6 6 10 
7 3 7 
8 4 8 
9 9 5 
10 10 6 
Here we are assuming that 0 is the Initial state then based on parity we will proceed further
 suppose if the parity is 0 then we move to the 1 state but if the parity bit is 1 then we move to
the 2 state
 suppose if the parity is odd 0 then we move to the state 3 from the state 1 but if the parity is
odd 1 then we move to the state 4 from state 1
 suppose if the parity is even 0 then we move to the state 5 from the state 2 but if the parity is
even 1 then we move to the state 6 from the state 2
 once the parity is completed then we can proceed for the message and if it reaches the final
state then we need to append 1 otherwise append 0

Machine Testing:
A B C Parity
0010 1101 001 Odd0
Case 1: ABCB is the message whose binary value is 001011010011101
So initially we are in state 0, so first we look for the parity right now the parity is 0, so we move to the
state 1 further the parity is odd, so we move to the state 3 now we start our message so initial bit is 0 so
it move to the next state which is 7 now the next bit is 0 so it again move to the state number 3, next bit
is 1, and it is self-loop so it remains on same state i.e. 3 now next bit is 0 so it again move to the state 7
now again it receive next bit as 1 so again it is self-loop for two times then next bit is 1 so it move to the
state 3, next bit is 0 so move to state 7 again next bit is 0 move to the state 3 now there is three
continuous but it is self-loop so it does not affect and remains in the same state 3 now next bit is 0 so
move to the state 7 then final bit is 1 so remains in 7 states which is accepting state
So the encoded message is 0010110100111011
Case 2: BCB is the message whose binary value is 11010011101
So initially we are in state 0, so first we look for the parity right now the parity is 0 so we move to the
state 1 further the parity is odd, so we move to the state 3 now we start our message so initial bit is 1 so
we remains in the same state 3 next bit is also 1 so no need to move now the next bit is 0 so we need to
move the state 7 next bit is again 0 so move to the state 3 now there is three continuous 1 bit, so we
remain in the same state and further next is 0 so move to the state 3 and final bit is 1 so remains in the
same state, our string is over and right now we are in non-final state, so it is non-accepting
So the encoded message is 110100111010