49325 CAMD Assignment 1: Finite Element Analysis of Truss, UTS

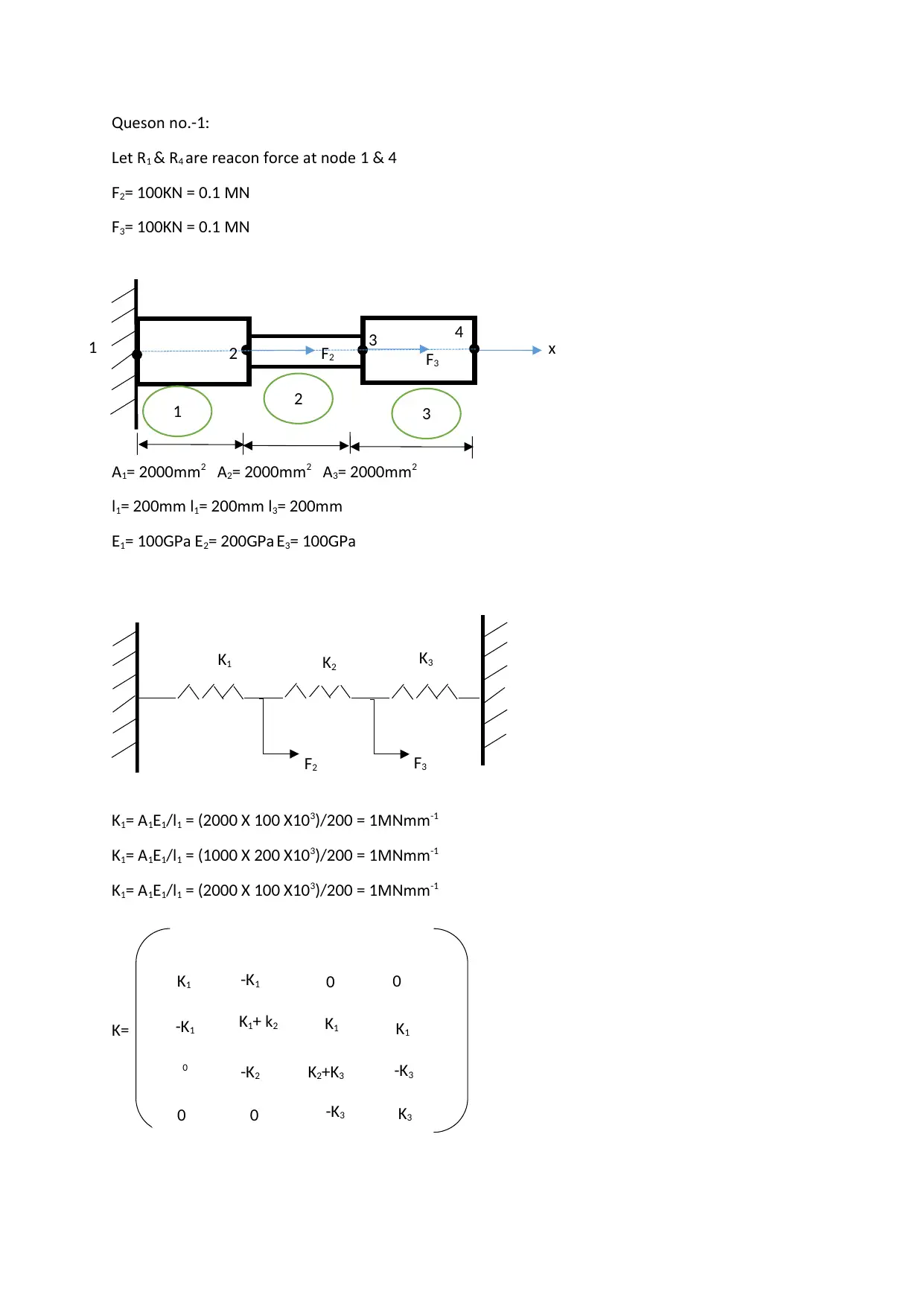
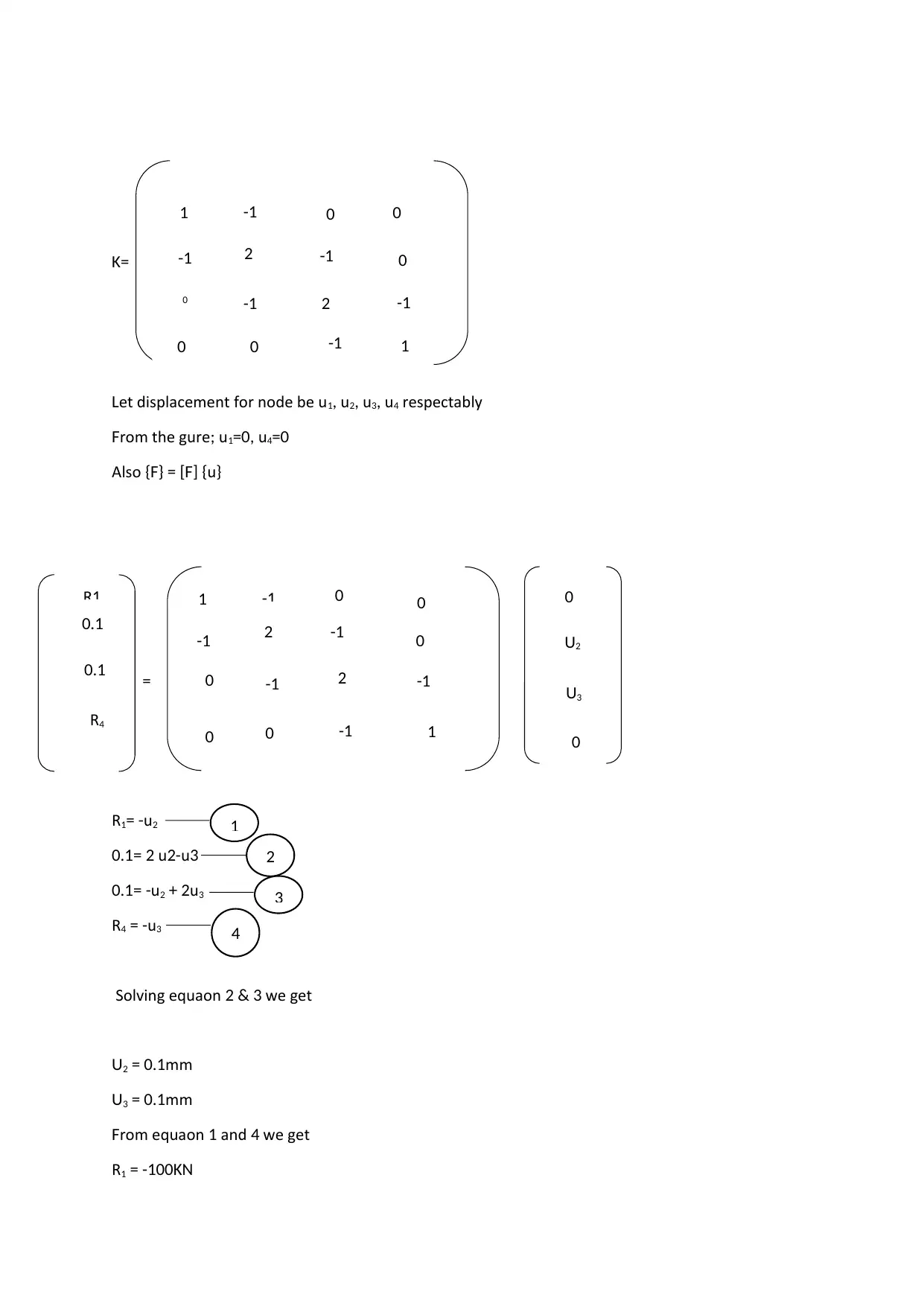
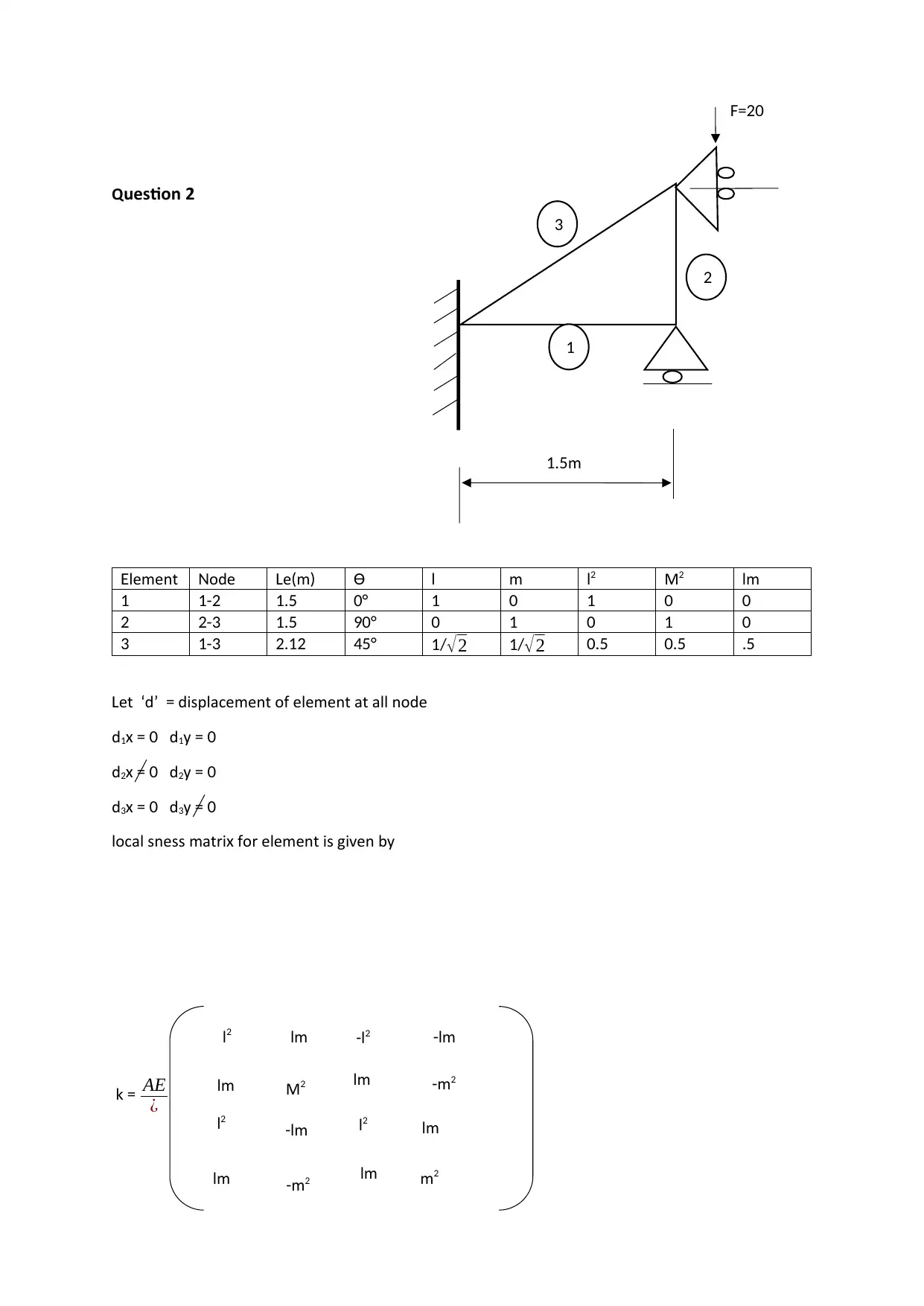
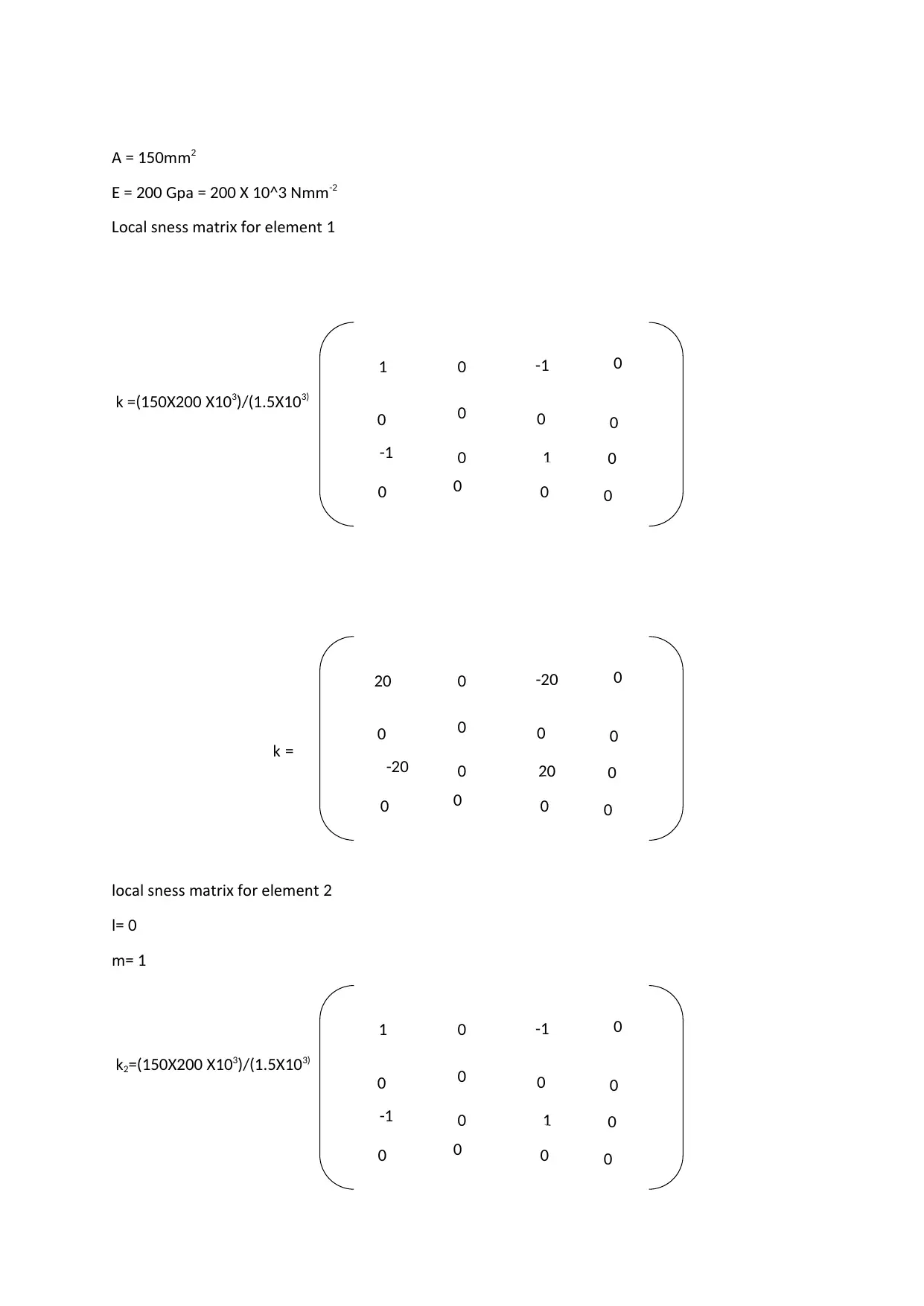
This document presents the solution to a Computer-Aided Mechanical Design (CAMD) assignment involving the analysis of truss structures using the Finite Element Method (FEM). The assignment includes two questions: the first involves a two-bar structural assemblage subjected to forces, requiring the determination of displacements, reaction forces, and normal stresses within the elements; the second question focuses on a plane truss structure, requiring the calculation of nodal displacements and stresses. The solution provides detailed hand calculations, stiffness matrices, and stress analysis for each element, with reference to established FEM principles. The analysis is based on the course 49325 Computer-Aided Mechanical Design at UTS.

CAMD
Document subtitle[ ]
DA[ TE]
Company name[ ]
Company address[ ]

uestion noQ .-1:
et RL 1 R& 4 are reaction force at node 1 & 4
F2 M= 100KN = 0.1 N
F3 M= 100KN = 0.1 N
A1 mm= 2000 2 A2 mm= 2000 2 A3 mm= 2000 2
l1 mm l= 200 1 mm l= 200 3 mm= 200
E1 a= 100GP E2 a= 200GP E3 a= 100GP
K1 A= 1E1 l/ 1 = (2000 X 100 X103 M mm)/200 = 1 N -1
K1 A= 1E1 l/ 1 = (1000 X 200 X103 M mm)/200 = 1 N -1
K1 A= 1E1 l/ 1 = (2000 X 100 X103 M mm)/200 = 1 N -1
K=
1 2 3 4
F2 F3
x
1 2 3
F3F2
K1 K2 K3
K1 -K1 0 0
-K1 K1 k+ 2 K1 K1
-K3K2+K3-K2
0
0 0 -K3 K3

K=
et displacement for node be uL 1 u, 2 u, 3 u, 4 respectably
rom the fi gure uF ; 1 u=0, 4=0
Also u{F} = [F] { }
=
R1 u= - 2
u u0.1= 2 2- 3
u0.1= - 2 u+ 2 3
R4 u= - 3
Solving equation we get2 & 3
U2 mm= 0.1
U3 mm= 0.1
rom equation and we getF 1 4
R1 = -100KN
1 -1 0 0
-1 2 -1 0
-12-10
0 0 -1 1
1 -1 0 0
-1 2 -1 0
-12-1
0 0 -1 1
R1
0.1
0.1
R4
0
0
U2
U3
0
1
2
3
4

R4 = -100KN
ormal stress in elementN 1
[ϵ1]= 1
l 1 [-1 1]
[ϵ1]= 1
l 1 [-1 1]
[ϵ1]= .1
200 = 0.0005
𝛔1= E1 ϵ1
𝛔1 pa M a= 100 X 0.0005 = 0.05 G = 50 P
ormal stress in elementN 2
[ϵ2]= 1
200 [-1 1]]
[ϵ2]= 0
𝛔2= 0
ormal stress in elementN 3
[ϵ3]= 1
200 [-1 1]
[ϵ3]= −0.0005
𝛔3= E3 ϵ3 a= 100 X (-0.0005) = -0.05GP
𝛔3 Mpa= -50
U1
U2
0
.1
0
.1
0.1
0

Question 2
lementE odeN e mL ( ) Ɵ l m l2 M2 lm
1 1-2 1.5 0° 1 0 1 0 0
2 2-3 1.5 90° 0 1 0 1 0
3 1-3 2.12 45° 1/√2 1/√2 0.5 0.5 .5
et d displacement of element at all nodeL ‘ ’ =
d1 dx = 0 1y = 0
d2 dx = 0 2y = 0
d3 dx = 0 3y = 0
local stiffness matri for element is given byx
k = AE
¿
3
2
1
F=20
m1.5
l2 lm l- 2 lm-
lm M2 lm m- 2
lml2
lm-l2
lm m- 2 lm m2

A mm= 150 2
pa mmE = 200 G = 200 X 10^3 N -2
ocal stiffness matri for elementL x 1
k =(150X200 X103)/(1.5X103)
k =
local stiffness matri for elementx 2
l= 0
m= 1
k2=(150X200 X103)/(1.5X103)
0
0 -1 01
0 0 0
010-1
0 0 0 0
0
0 -20 020
0 0 0
0200-20
0 0 0 0
0
0 -1 01
0 0 0
010-1
0 0 0 0

then
k2 =
local stiffness matri for elementx 3
k3=(150X200 X103)/(1.5X103)
then
k3 =
e know thatW
d{F} = [K]{ }
0
0 0 00
20 0 -20
0000
0 -20 0 20
.5
.5 -.5 -.5.5
0.5 -.5 -.5
.5.5-.5-.5
-.5 -.5 0.5 0.5
7.08
7.08 -20 027.08
7.08 0 -20
0200-20
0 0 0 20
-7.08 -7.08
-7.08
0
-7.08
0
0
-7.08
-7.08
-7.08
-7.08
0
0
0
-20
7.08
7.08
-20
7.08
7.08

F1x = 0 F1y = 0
F2x = 0 F2y = 0
F3x = 0 F3y = -20KN
then
=
rom the above matri we getF x
d2x = 0
d3y = 20/7.08
mm= 2.825
odal displacement for stress element is given byN 2
d2 dx = 0 2y = 0
d3 dx = 0 3y mm= 2.825
Stress 𝛔= E
Lc m l m d[-1 - ]{ }
𝛔2= 200 X 103
1.5 X 103 [0 -1 0 1 ]
𝛔2= 400
3 [0 -1 0 1 ]
7.08
7.08 -20 027.08
7.08 0 -20
0200-20
0 0 0 20
-7.08 -7.08
-7.08
0
-7.08
0
0
-7.08
-7.08
-7.08
-7.08
0
0
0
-20
7.08
7.08
-20
7.08
7.08
0
0
0
-20
0
0
0
0
0
d2x
0
0
d3x
d2x
d2y
d3x
d3y
0
0
0

𝛔2= (400X2.825)/3
M a=376.67 P R et al( ., ., 2014)
References
R Chandrupatla D A elegundu., T., , ., . & B , 2014. ntroduction to inite Elements in EngineeringI F :
nternational EditionI . ew ork City earson ducation imitedN Y : P E L .
2.85