Finite Math - University Project: Cookie Production Optimization

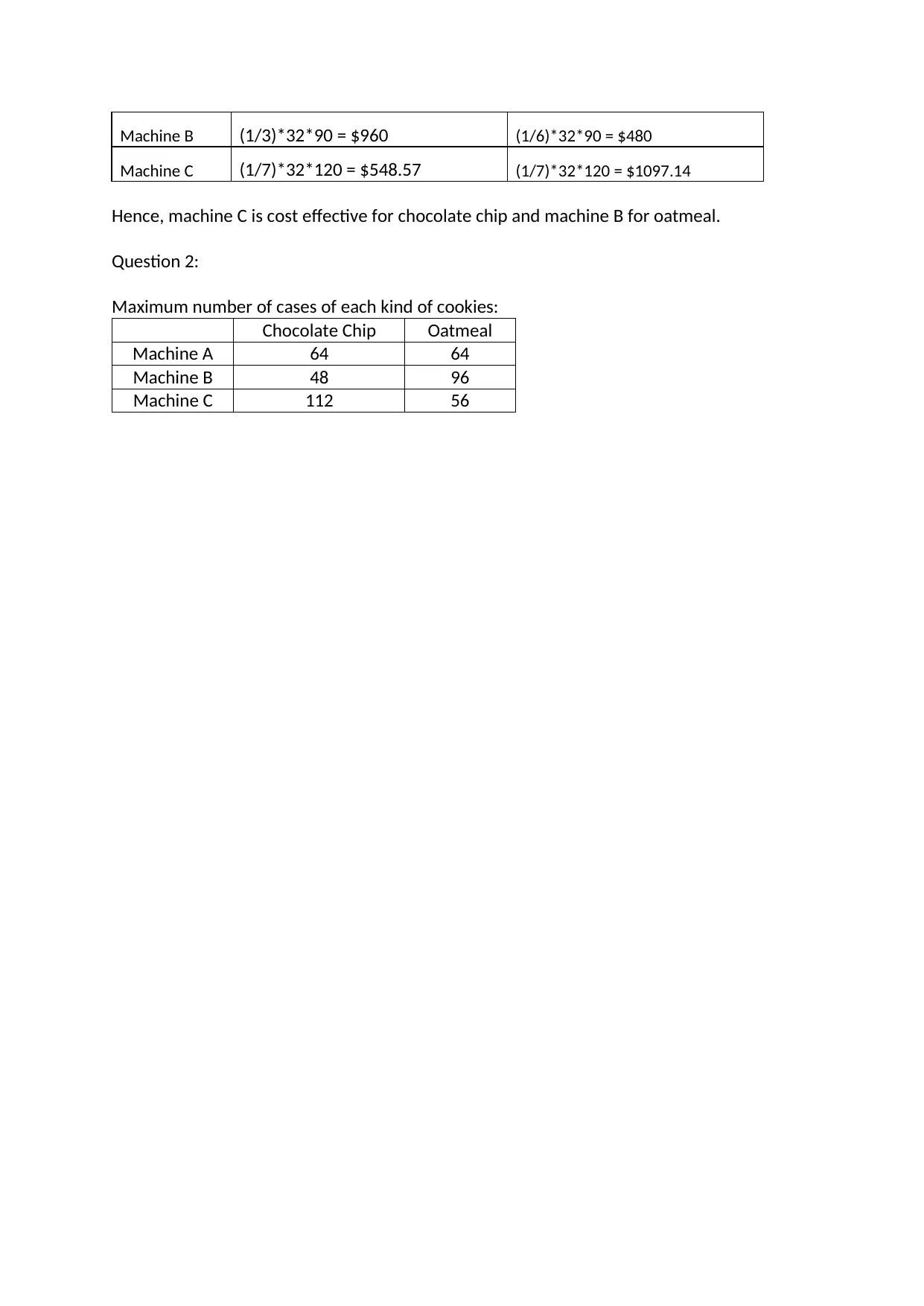
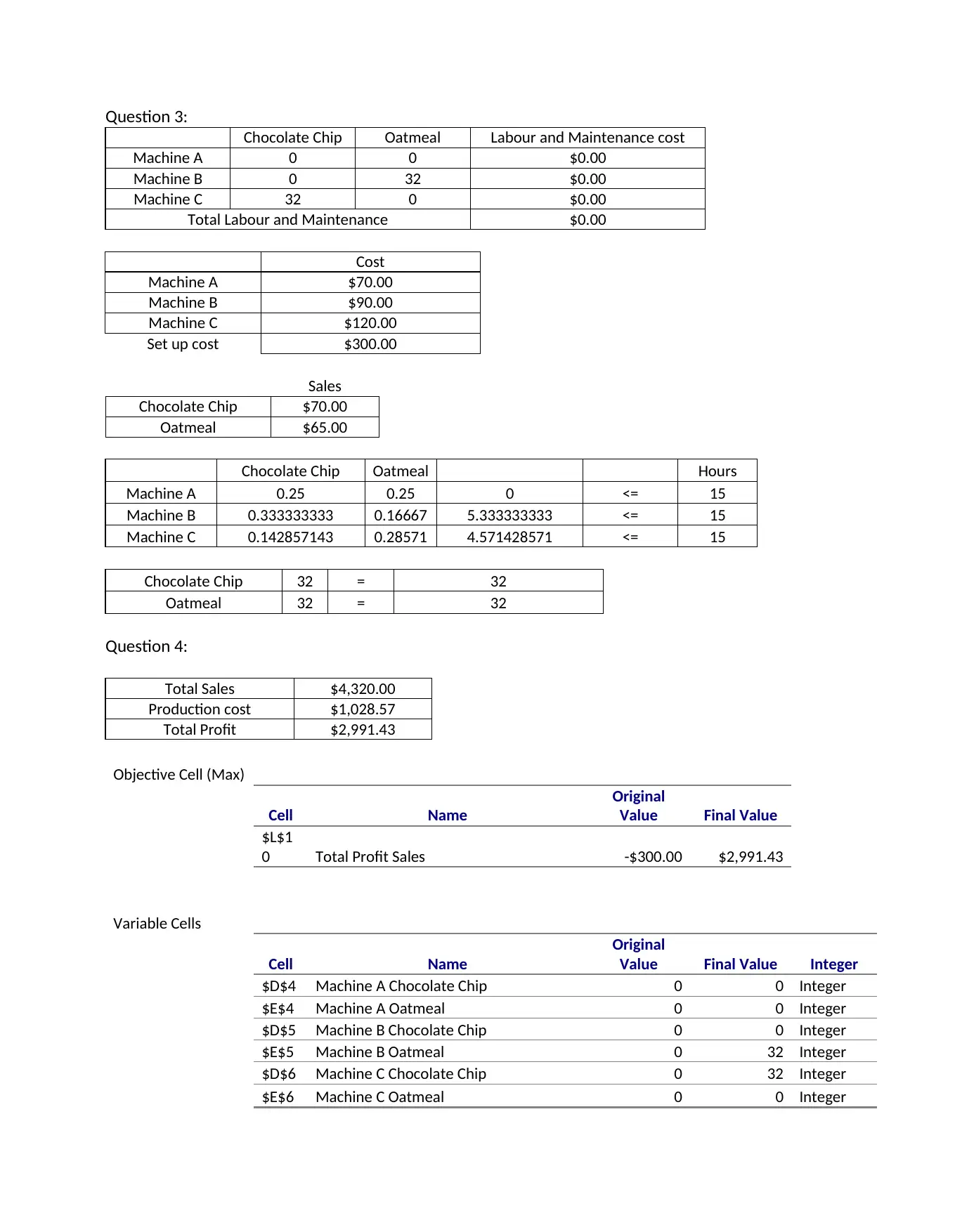
This Finite Math project uses linear programming to optimize cookie production. The student formulates an objective function to maximize profit based on the sales revenue of chocolate chip and oatmeal raisin cookies, considering production constraints for three machines (A, B, and C). The project employs a graphical method to solve the linear programming problem, identifying the feasible region and optimal solution. The analysis determines the optimal combination of cookie types (32 cases each) to maximize profit. Part B of the project delves deeper, analyzing machine effectiveness for each cookie type, determining maximum production limits, calculating labor and maintenance costs, and evaluating total profit using solver tools. The project concludes with a summary of the optimal production plan and relevant bibliography.

Finite Math – Unit 3 Project
Name of the Student
Name of the University
Author Note

Part A:
Here, CC denotes the chocolate chip and OR denotes oatmeal raisin.
Also, per case CC = $70 and per case OR = $65.
Hence, total sales revenue is 70*CC + 65*OR
Therefore, the objective function will be
Max Z = 70*CC + 65*OR
All three machines, Machine A, Machine B and Machine C can be used for production.
However, there are few constraints as mentioned below:
For machine A: (1/4)*CC + (1/4)*OR <= 16
Or, CC + OR <= 64 ……… (1)
For machine B: (1/3)*CC + (1/6)*OR <= 16
Or, 2CC + OR <= 96 …….. (2)
For machine C: (1/7)*CC + (2/7)*OR <= 16
Or, CC + 2OR <= 112 ……. (3)
Therefore, in summary the problem will be
Max Z = 70CC + 65OR
Subject to
CC + OR <= 64 ……… (1)
2CC + OR <= 96 …….. (2)
CC + 2OR <= 112 ……. (3)
CC, OR >= 0
Here graphical method has been used to solve this problem:
Step 1: converting inequalities into equations
From (1), we have
CC + OR = 64 …….. (4)
Putting, CC = 0, we have OR = 64; similarly putting OR = 0, we have CC = 64
Hence, equation (4) will intersect y-axis and x-axis at (0, 64) and (64, 0) respectively.
From (2), we have
2CC + OR = 96 …….. (5)
Putting, CC = 0, we have OR = 96; similarly putting OR = 0, we have CC = 48
Hence, equation (5) will intersect y-axis and x-axis at (0, 96) and (48, 0) respectively.
From (3), we have
CC + 2OR = 112 …….. (6)
Putting, CC = 0, we have OR = 56; similarly putting OR = 0, we have CC = 112
Hence, equation (6) will intersect y-axis and x-axis at (0, 56) and (112, 0) respectively.
Now, plotting these equations into graph, we have the feasible region as OXYZAO

Now, the vertices can be find out considering the intersection theory
Here, X is (0, 56); A is (48, 0), O is (0, 0)
B is intersection point of (4) and (6)
Applying intersection theory, we have y = 48 and x = 16
That is Y is (16, 48)
Similarly, Z is the intersection point of (4) and (5)
Applying intersection theory, we have x = 32 and y = 32
That is, Z is (32, 32)
Now, at O, Z = 0
At X, Z = 0*70 + 56*65 = 3640
At Y, Z = 16*70 + 48*65 = 4240
At Z, Z = 32*70 + 32*65 = 4320
At A = 48*70 + 0*65 = 3360
Hence, Z is the optimal point. In other words, the optimum combination of chocolate chip
and oatmeal raisin is 32 cases each.
Part B:
Question 1:
Chocolate Chip Oatmeal
Machine A (1/4)*32*70 = $560 (1/4)*32*70 = $560

Machine B (1/3)*32*90 = $960 (1/6)*32*90 = $480
Machine C (1/7)*32*120 = $548.57 (1/7)*32*120 = $1097.14
Hence, machine C is cost effective for chocolate chip and machine B for oatmeal.
Question 2:
Maximum number of cases of each kind of cookies:
Chocolate Chip Oatmeal
Machine A 64 64
Machine B 48 96
Machine C 112 56

Question 3:
Chocolate Chip Oatmeal Labour and Maintenance cost
Machine A 0 0 $0.00
Machine B 0 32 $0.00
Machine C 32 0 $0.00
Total Labour and Maintenance $0.00
Cost
Machine A $70.00
Machine B $90.00
Machine C $120.00
Set up cost $300.00
Sales
Chocolate Chip $70.00
Oatmeal $65.00
Chocolate Chip Oatmeal Hours
Machine A 0.25 0.25 0 <= 15
Machine B 0.333333333 0.16667 5.333333333 <= 15
Machine C 0.142857143 0.28571 4.571428571 <= 15
Chocolate Chip 32 = 32
Oatmeal 32 = 32
Question 4:
Total Sales $4,320.00
Production cost $1,028.57
Total Profit $2,991.43
Objective Cell (Max)
Cell Name
Original
Value Final Value
$L$1
0 Total Profit Sales -$300.00 $2,991.43
Variable Cells
Cell Name
Original
Value Final Value Integer
$D$4 Machine A Chocolate Chip 0 0 Integer
$E$4 Machine A Oatmeal 0 0 Integer
$D$5 Machine B Chocolate Chip 0 0 Integer
$E$5 Machine B Oatmeal 0 32 Integer
$D$6 Machine C Chocolate Chip 0 32 Integer
$E$6 Machine C Oatmeal 0 0 Integer

From the above calculations, it can be said that the company can earn $2,991.43 as profit
Question 5:
The maximum limit of chocolate chips can be produced is 60 units and in such case there will be no additional
profit as the number of cases of Oatmeal chips will be reduced to attain maximum profit.

Bibliography
Paris, Q., 2016. An economic interpretation of linear programming. Springer.
Sanchez, L.C. and Herrera, J., 2016. Solution to the multiple products transportation problem: linear
programming optimization with Excel Solver. IEEE Latin America Transactions, 14(2), pp.1018-1023.
Uko, L.U., Lutz, R.J. and Weisel, J.A., 2017. An Application of Linear Programming in Performance
Evaluation. Academy of Educational Leadership Journal.
Wisniewski, M. and Klein, J.H., 2017. Critical Path Analysis and Linear Programming. Macmillan
International Higher Education.