Analysis of London Temperature Data and Forecasting (Numeracy & Data)

This assignment analyzes temperature data collected in London from March 10th to March 19th, 2022. The solution begins by organizing the temperature readings into a table format, followed by visual representations using column and line charts. The core of the assignment involves the application of statistical tools and techniques to analyze the data, including calculating the mean, median, mode, range, and standard deviation. A linear forecasting model is then employed to predict future temperatures, specifically forecasting the temperatures for the 11th and 14th days. The solution concludes with a list of references to support the methods and concepts used in the analysis.

NUMERACY & DATA
ANALYSIS

Table of Contents
Collection of data pertaining to the temperature of London for the ten consecutive days..........3
1. Arrangement of data in a table format.....................................................................................3
2. Presenting the data through charts...........................................................................................3
3. Analysis of data through statistical tools & techniques...........................................................4
4. Linear Forecasting model to forecast future Temperature within the London City................8
REFERENCES..............................................................................................................................10
Books and Journals....................................................................................................................10

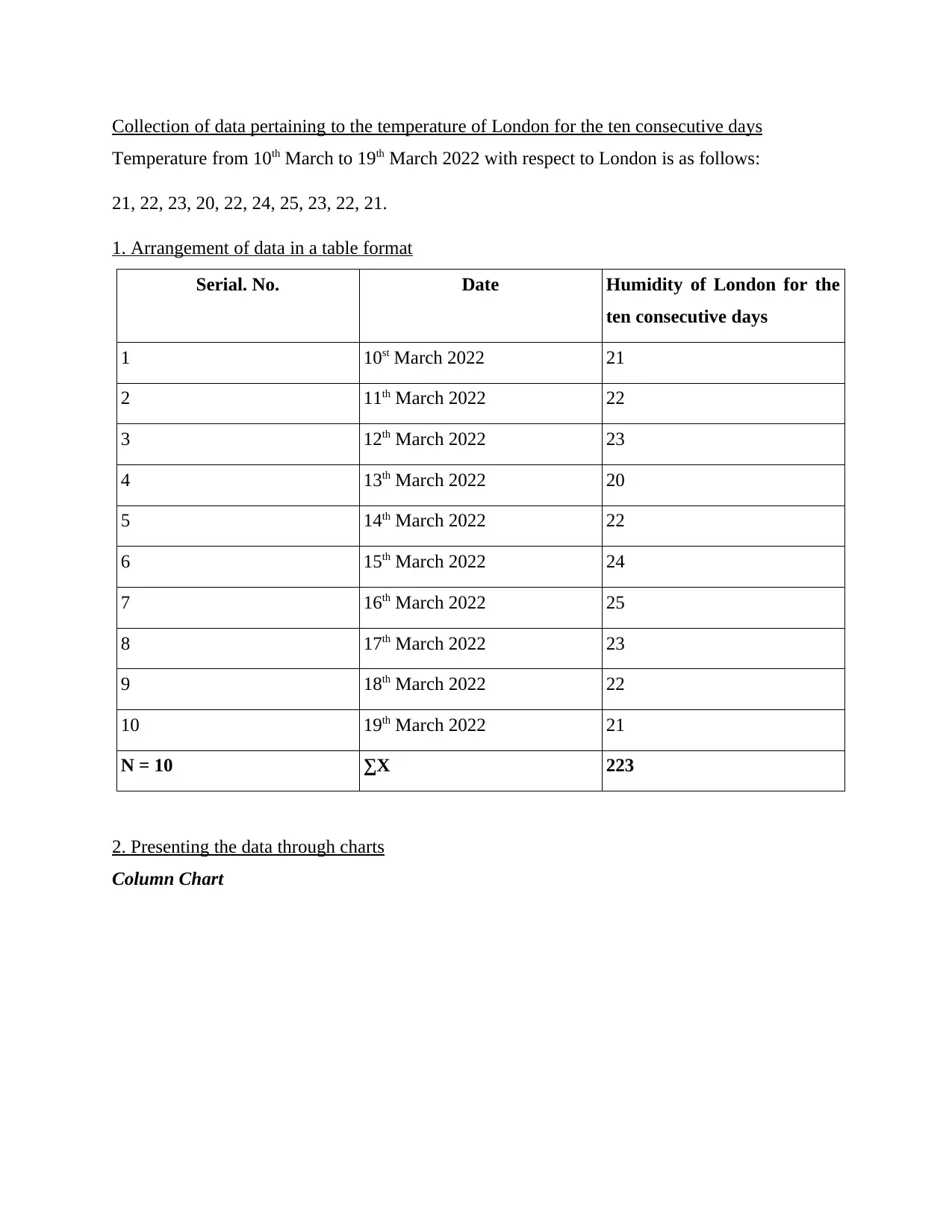
Collection of data pertaining to the temperature of London for the ten consecutive days
Temperature from 10th March to 19th March 2022 with respect to London is as follows:
21, 22, 23, 20, 22, 24, 25, 23, 22, 21.
1. Arrangement of data in a table format
Serial. No. Date Humidity of London for the
ten consecutive days
1 10st March 2022 21
2 11th March 2022 22
3 12th March 2022 23
4 13th March 2022 20
5 14th March 2022 22
6 15th March 2022 24
7 16th March 2022 25
8 17th March 2022 23
9 18th March 2022 22
10 19th March 2022 21
N = 10 ∑X 223
2. Presenting the data through charts
Column Chart

10st March
2022
11th
March
2022
12th
March
2022
13th
March
2022
14th
March
2022
15th
March
2022
16th
March
2022
17th
March
2022
18th
March
2022
19th
March
2022
21 22 23
20
22
24 25
23 22 21
Humidity of London for the ten consecutive days
Line Chart
10st March
2022
11th
March
2022
12th
March
2022
13th
March
2022
14th
March
2022
15th
March
2022
16th
March
2022
17th
March
2022
18th
March
2022
19th
March
2022
21 22 23
20
22
24 25
23 22 21
Humidity of London for the ten consecutive days
3. Analysis of data through statistical tools & techniques
Mean: It refers to the average value representing the observations forming part of the data set. It
is calculated by summing up the value of all observation and dividing the resulting sum with the
number of observations in a data set (Chakrabarty, 2021). In this way, mean is determined as a
single value which represents the entire set of data. The symbol of mean is known as x bar
indicated as x̄.
Formula for mean = x̄ = ∑X / n

∑X = 21 + 22 + 23 + 20 + 22 + 24 + 25 + 23 + 22 + 21 = 223
n = 10
x̄ = 223 / 10 = 22.3
Median: It refers to the middle value of the data set which can be obtained through arranging the
data in either descending or ascending order. Median value is the one where 50% values are both
above & below it (Black and Masten, 2020).
For the data set containing even number of observations, the median can be determined
through summing up the two numbers lying in the middle & dividing the same by 2.
Median for the data set concerning the temperature of ten consecutive days has been determined
as follows:
Serial No. Temperature data arranged in
ascending order
1 20
2 21
3 21
4 22
5 22
6 22
7 23
8 23
9 24
10 25

The above data set consists of even number of observation that is, 10 and the two numbers lying
in the middle are 22 and 22. Therefore, by adding them together and dividing the resulting sum
by two will give the median for this data.
Median = 22 + 22 / 2 = 44 / 2 = 22.
Mode: It is that value of the data set which have appeared most frequently. Also, the modal
value can be defined as the the value which have occurred for most of the time within the data
set. Accordingly, 22 is identified as the mode for the data concerning the temperature of
London city as it is the most frequently appearing value of the data series.
Range: It is the basic measure of dispersion among the data set. Range can be obtained through
subtracting the lowest value from the highest value within the data set (Beyer, 2021). The highest
value in the temperature data is identified as 25 and the lowest value identified is 20.
Accordingly, the range of this data set is 25 – 20 = 5.
Standard deviation: It is the another measure of dispersion with the help of which the variation
between the mean value and all the data points with the data set are determined (Kaur, Stoltzfus
and Yellapu, 2018). When the data points are situated closer to the mean, then the value of
standard deviation would be small or vice. Also, the small value of standard deviation indicates
that the mean value is representing the data set well.
The steps that are useful in determining the standard deviation are as follows:
 Calculation of mean value for the data set.
 Subtracting the mean value from all the individual values of the series and squaring the
result.
 Summing up the squared value along with dividing it with the number of observations.
 Placing the result obtained in step 3 under the square root will give the standard deviation
of the data set.
Formula
σ =

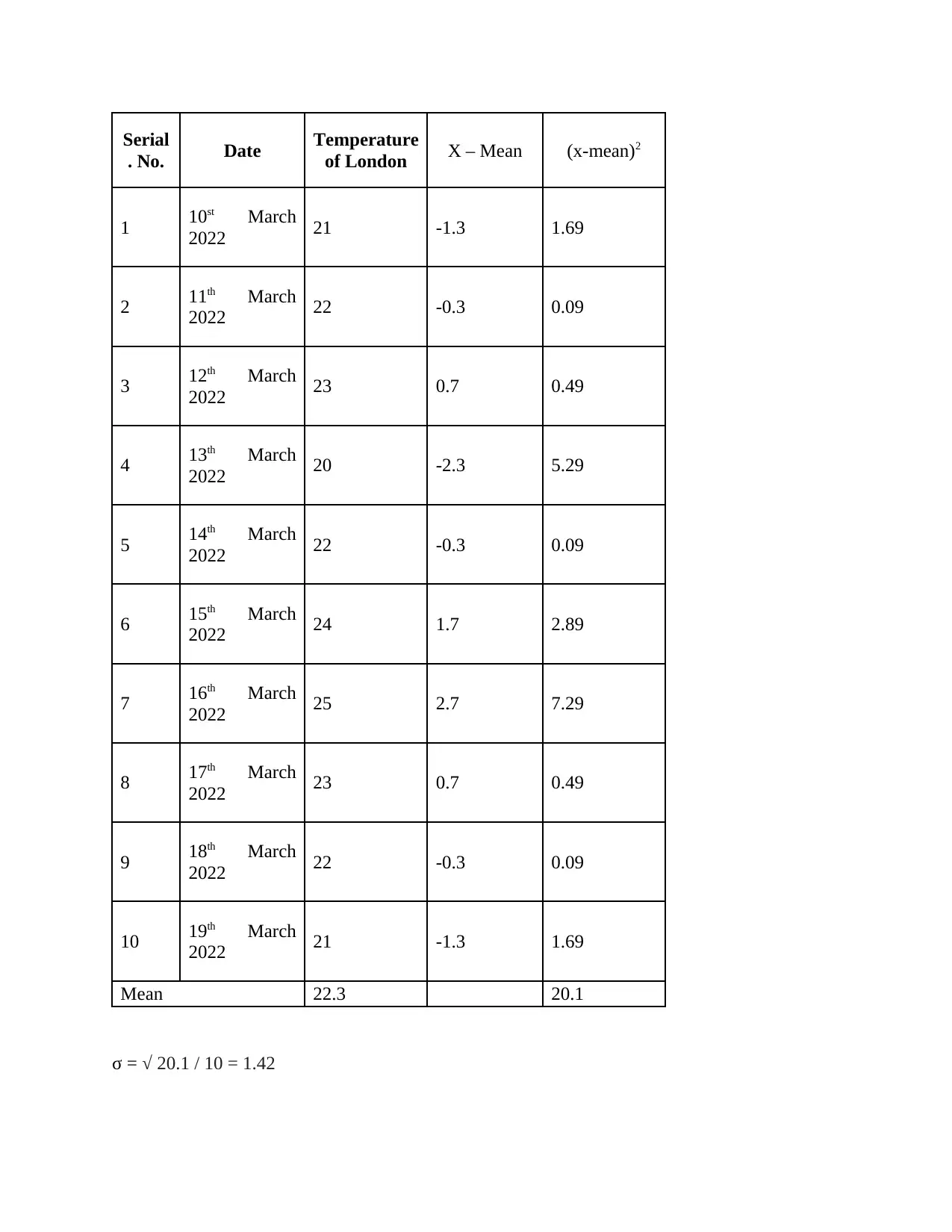
Serial
. No. Date Temperature
of London X – Mean (x-mean)2
1 10st March
2022 21 -1.3 1.69
2 11th March
2022 22 -0.3 0.09
3 12th March
2022 23 0.7 0.49
4 13th March
2022 20 -2.3 5.29
5 14th March
2022 22 -0.3 0.09
6 15th March
2022 24 1.7 2.89
7 16th March
2022 25 2.7 7.29
8 17th March
2022 23 0.7 0.49
9 18th March
2022 22 -0.3 0.09
10 19th March
2022 21 -1.3 1.69
Mean 22.3 20.1
σ = √ 20.1 / 10 = 1.42

4. Linear Forecasting model to forecast future Temperature within the London City
Linear forecasting model = y = mx + c
Serial.
No.
X
Temperature
of London Y
xy x2
1 21 21 1
2 22 44 4
3 23 69 9
4 20 80 16
5 22 110 25
6 24 144 36
7 25 175 49
8 23 184 64
9 22 198 81
10 21 210 100
55 223 1235 385
I. Calculation of the value of m – Steps
m =
m = (10 * 1235) – (55 * 223) / (10 * 385) – (55)2
m = 12350 – 12265 / 3850 – 3025
m = 85 / 825 = 0.10
m is the indicator of steepness within the linear model. Accordingly, indicates the regression
line’s direction (Farebrother, 2020).
II. Calculation of the value of c – Steps
c=
c = 223 – (0.10 * 55) / 10

c = 223 – 5.5 / 10
c = 217.5 / 10 = 21.75
C is the constant value of the linear forecasting model and shows the distance between starting
point of y-axis and origin.
 Forecasting Temperature for 11th and 14th day
x = 11th day
y = mx +c
y = 0.1 * 11 + 21.75
y = 1.1 + 21.75 = 22.85
x = 14th day
y = 0.1 * 14 + 21.75
y = 1.4 + 21.75 = 23.15
Therefore, temperature in London on 11th & 14th day would be 22.85 and 23.15 respectively.

REFERENCES
Books and Journals
Beyer, A., 2021. Measures of Central Tendency. Introduction to Statistics for Psychology.
Black, W. H. and Masten, L. B., 2020. Empirical Investigation of Alternative Measures of
Central Tendency. Journal of Forensic Accounting Research, 5(1), pp.216-256.
Chakrabarty, D., 2021. Measuremental Data: Seven Measures of Central
Tendency. International Journal of Electronics, 8(1).
Farebrother, R. W., 2020. Neopythagorean approaches to measures of central tendency and
dispersion. Chance, 33(1), pp.26-29.
Kaur, P., Stoltzfus, J. and Yellapu, V., 2018. Descriptive statistics. International Journal of
Academic Medicine, 4(1), p.60.