Frequency Response & Bode Plots Analysis - Electrical Engineering

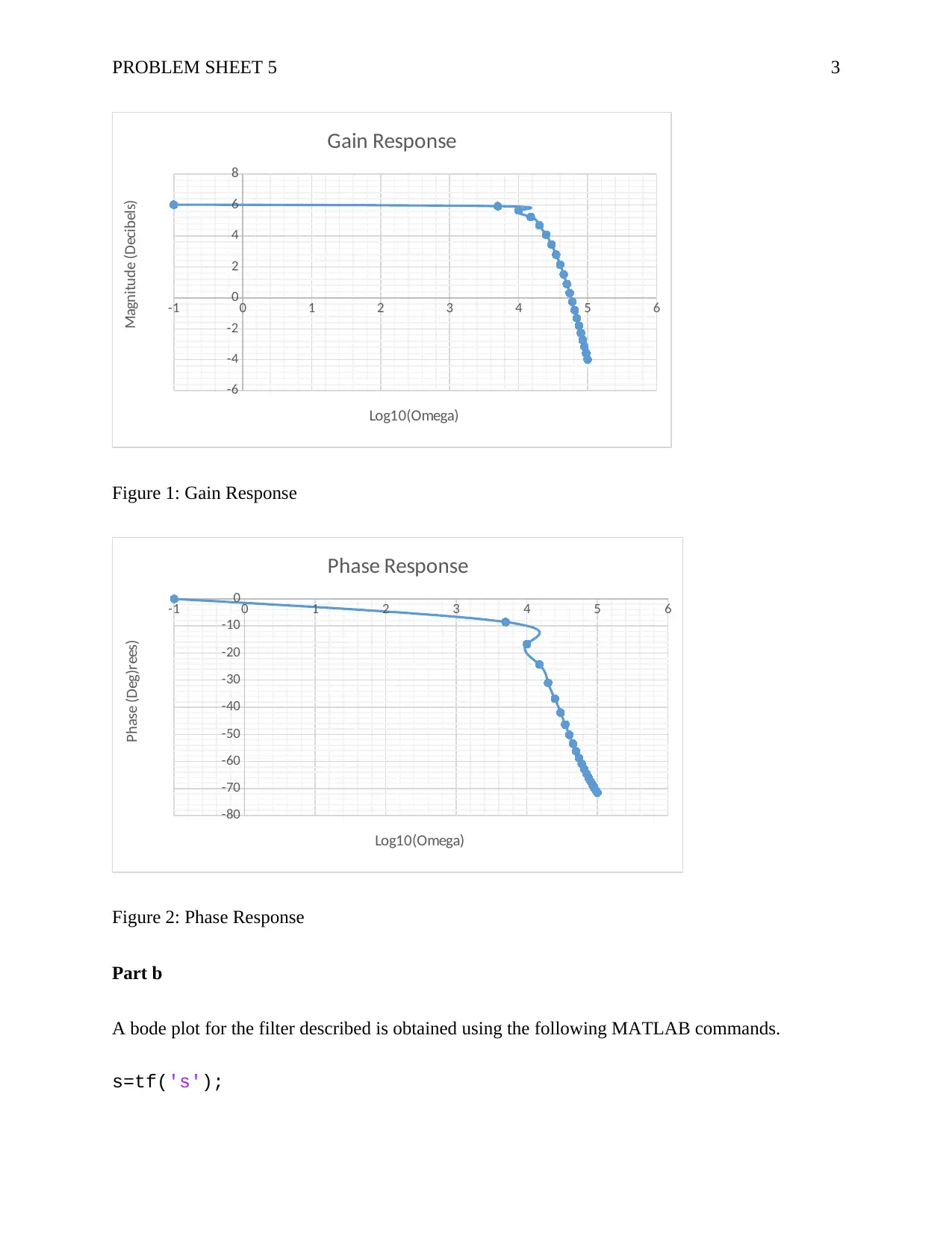
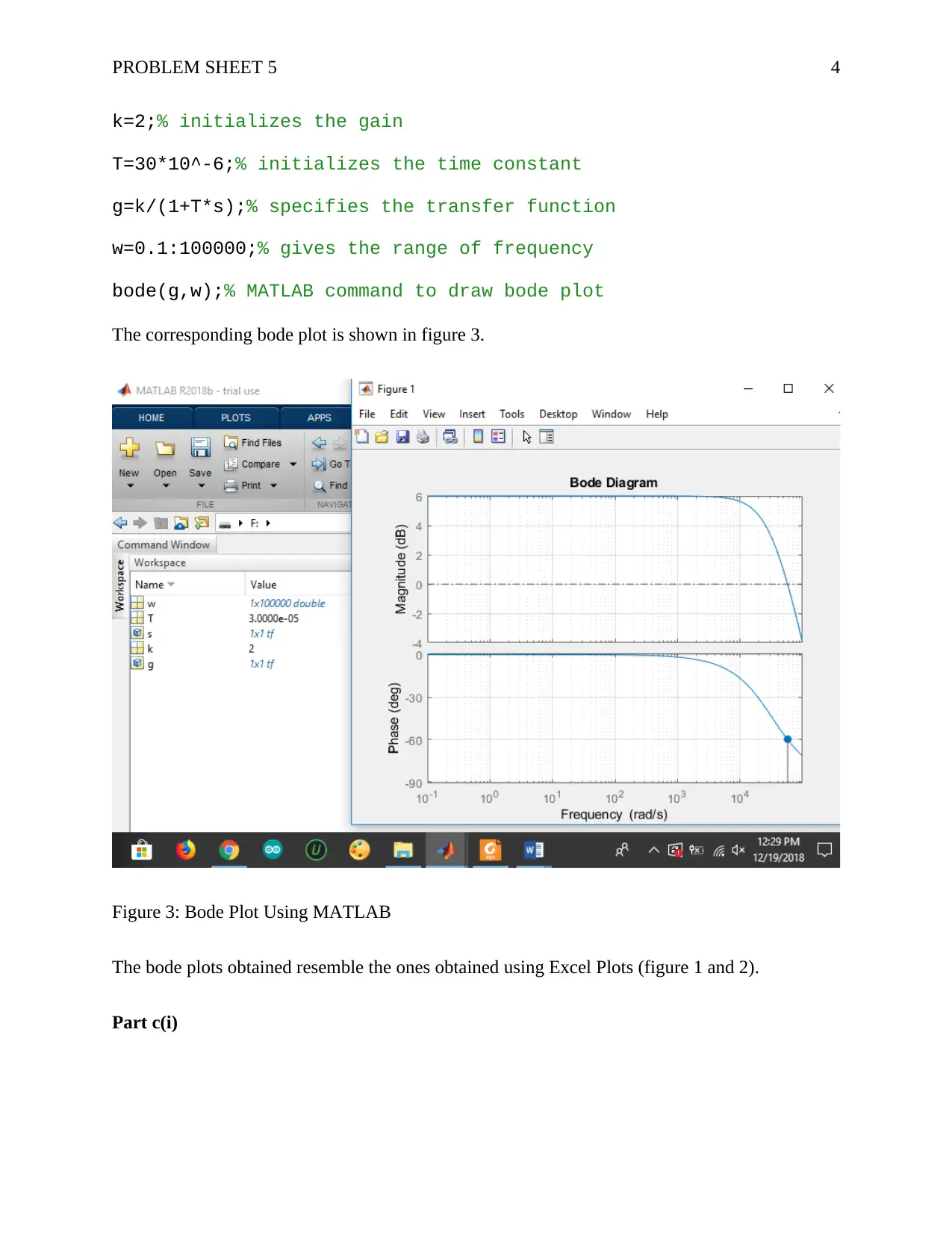
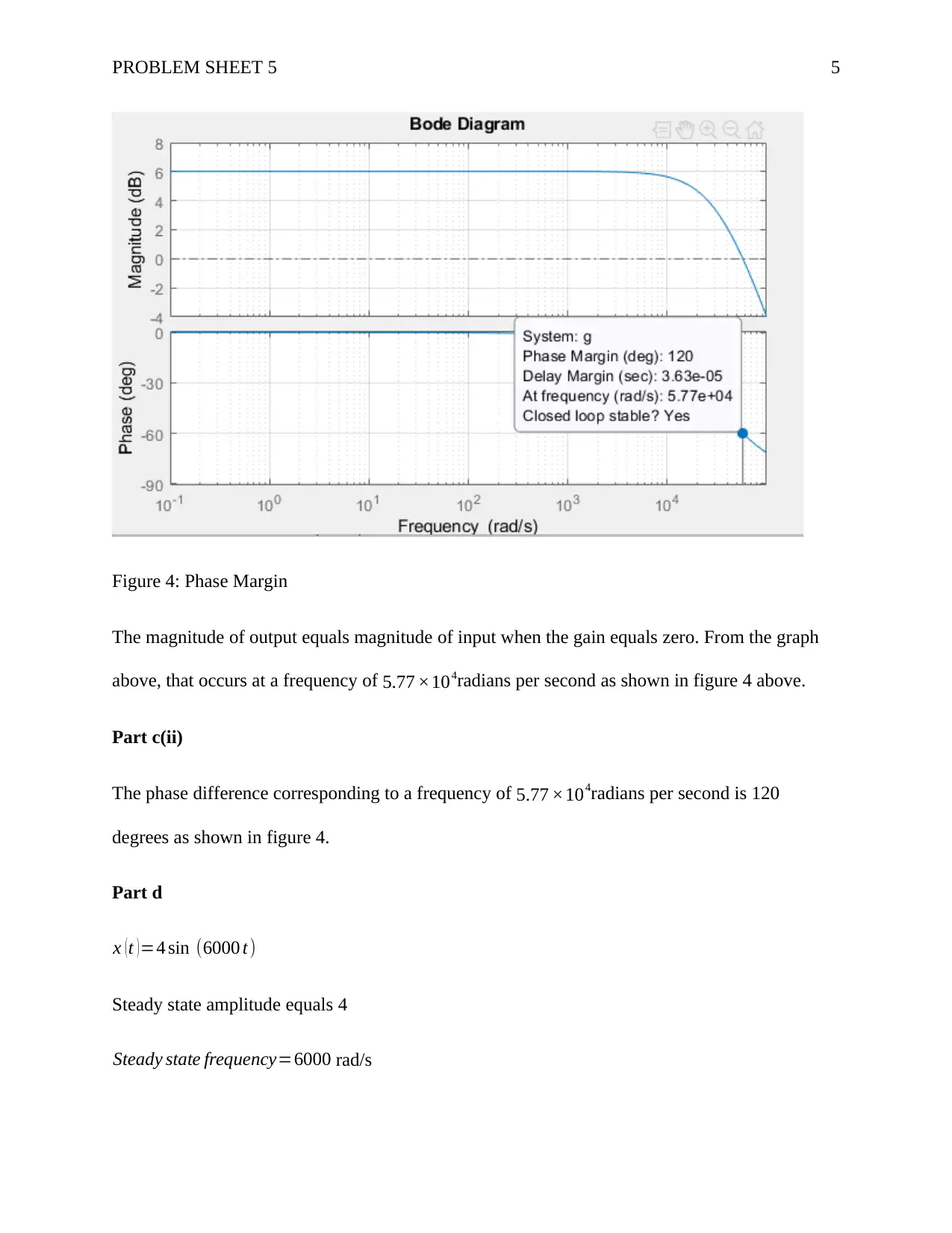
This assignment solution addresses Problem Sheet 5, focusing on the frequency response of a first-order filter with a gain of 2 and a time constant of 30μs. The solution involves using the Frequency Response Theorem to compute the gain and phase response, generating Bode plots using both Excel and MATLAB, determining the frequency at which the output magnitude equals the input magnitude, and calculating the corresponding phase difference. Additionally, the response to a sinusoidal input signal is analyzed, and the steady-state amplitude and frequency are determined. The solution includes MATLAB code, plots, and detailed mathematical derivations, providing a comprehensive analysis of the filter's behavior. Desklib provides a platform for students to access such solved assignments and study materials.

Running head: PROBLEM SHEET 5 1
Problem Sheet 5
Name
Institution

PROBLEM SHEET 5 2
Part a
Gain , k=2
Time Constant ,T =30 μs
G(s)= k
1+Ts = 2
1+30 ×10−6 s
Applying the frequency response theorem to the above equation yields:
G ( jω ) = K
1+ω2 T 2 − j ωKT
1+ω2 T 2 = 2
1+ω2 ( 30 ×10−6 ) 2 − j ω(2 ×30 ×10−6)
1+ ω2 ( 30× 10−6 ) 2
¿ 2
1+ 9× 10−10 ω2 − j 6 ×10−5 ω
1+ 9 ×10−10 ω2
|G ( jω )|= K
√1+ω2 T 2 = 2
√1+9 ×10−10 ω2 =20 log 2
√1+ 9 ×10−10 ω2 decibels
arg ( G ( jω ) )=tan−1 {−30 ×10−6 ω }= 180
π tan−1 {−30 ×10−6 ω } degrees
The gain and Phase response plots are shown in figure 1 and figure 2 below.

PROBLEM SHEET 5 3
-1 0 1 2 3 4 5 6
-6
-4
-2
0
2
4
6
8
Gain Response
Log10(Omega)
Magnitude (Decibels)
Figure 1: Gain Response
-1 0 1 2 3 4 5 6
-80
-70
-60
-50
-40
-30
-20
-10
0
Phase Response
Log10(Omega)
Phase (Deg)rees)
Figure 2: Phase Response
Part b
A bode plot for the filter described is obtained using the following MATLAB commands.
s=tf('s');

PROBLEM SHEET 5 4
k=2;% initializes the gain
T=30*10^-6;% initializes the time constant
g=k/(1+T*s);% specifies the transfer function
w=0.1:100000;% gives the range of frequency
bode(g,w);% MATLAB command to draw bode plot
The corresponding bode plot is shown in figure 3.
Figure 3: Bode Plot Using MATLAB
The bode plots obtained resemble the ones obtained using Excel Plots (figure 1 and 2).
Part c(i)

PROBLEM SHEET 5 5
Figure 4: Phase Margin
The magnitude of output equals magnitude of input when the gain equals zero. From the graph
above, that occurs at a frequency of 5.77 ×104radians per second as shown in figure 4 above.
Part c(ii)
The phase difference corresponding to a frequency of 5.77 ×104radians per second is 120
degrees as shown in figure 4.
Part d
x (t )=4 sin (6000 t)
Steady state amplitude equals 4
Steady state frequency=6000 rad/s

PROBLEM SHEET 5 6
Part e
x ( t ) =4 sin (6000 t)
X ( s ) =4. 6000
s2 [phone] = 24000
s2 [phone]
Y ( s )= 2
1+30 ×10−6 s X ( s )= 2
1+30 ×10−6 s × 24000
s2 [phone]
Y ( s ) = 48000
( s¿ ¿ 2+36 × 10−6 )(1+30 ×10−6 s)¿
y ( t )
x(t)=2 L−1
{ 1
1+30 ×10−6 s }= 2
30× 10−6 e
−t
30 ×10−6
y ( t ) = 2 x (t)
30 ×10−6 e
−t
30 ×10−6
y ( t ) =2 × 4 sin (6000 t)
30× 10−6 e
−t
30× 10−6
y ( t ) =8 sin (6000 t)
30 ×10−6 e
−t
30 ×10−6