Comprehensive Solutions: Functions, Modeling, and Asymptotes

This assignment solution covers various aspects of mathematical functions and modeling, including the identification of linear, cubic, and quadratic functions based on their rates of change. It includes the application of cubic regression models to analyze trends, such as cigarette use, and determines extreme values. The solution also explores power regression models to understand the relationship between animal mass and relative speed, along with calculations for specific scenarios like zebra mass. Furthermore, it addresses the concepts of vertical and horizontal asymptotes and provides a detailed analysis of drug concentration in the bloodstream, including maximum concentration, time to reach maximum concentration, and asymptote equations. Desklib offers a wide array of solved assignments and past papers for students seeking academic assistance.

Question 1
f(x) is a linear function since the rate of change remains same for all the values. For every 1 unit
increase in the value of x, f(x) tends to increase by 2 units.
g(x) is a cubic function with two roots as -1 and 0. Also, the rate of change does not tend to
follow any uniform pattern with the values first decreasing and then increasing. Further, the rate
of change also provides indication of concavity in the function.
h(x) is a quadratic function since rate of change while not being constant follows a pattern
whereby it continues to decrease by 2 units. For instance, as x increases from -5 to -4, h(x)
decreases by 14 units. Further increase in x decreases h(x) by 12 units, then 10 units and so on.
Question 2
a. Scatter plot
1

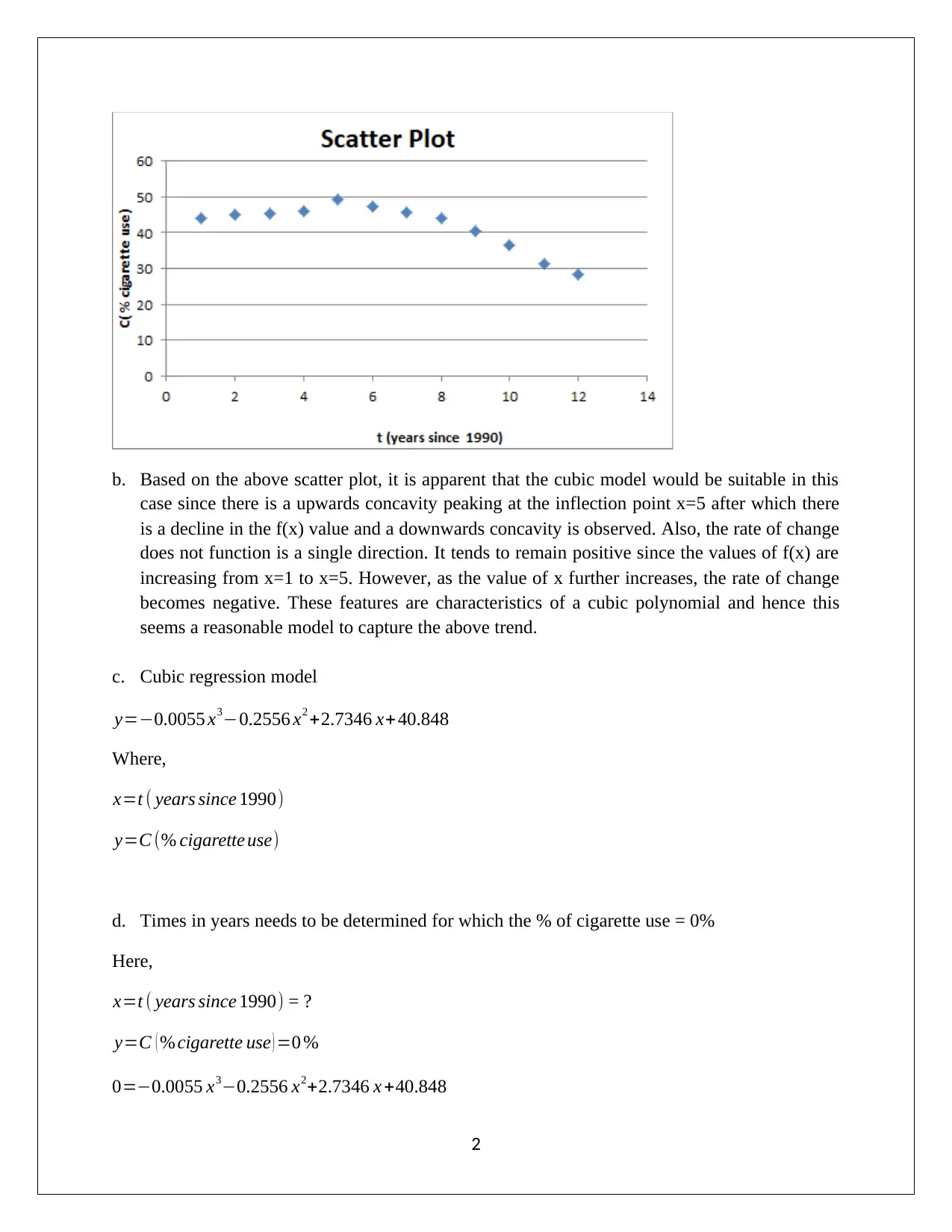
b. Based on the above scatter plot, it is apparent that the cubic model would be suitable in this
case since there is a upwards concavity peaking at the inflection point x=5 after which there
is a decline in the f(x) value and a downwards concavity is observed. Also, the rate of change
does not function is a single direction. It tends to remain positive since the values of f(x) are
increasing from x=1 to x=5. However, as the value of x further increases, the rate of change
becomes negative. These features are characteristics of a cubic polynomial and hence this
seems a reasonable model to capture the above trend.
c. Cubic regression model
y=−0.0055 x3−0.2556 x2 +2.7346 x+40.848
Where,
x=t ( years since 1990)
y=C (% cigarette use)
d. Times in years needs to be determined for which the % of cigarette use = 0%
Here,
x=t ( years since 1990) = ?
y=C ( %cigarette use ) =0 %
0=−0.0055 x3−0.2556 x2+2.7346 x +40.848
2

0.0055 x3+ 0.2556 x2−2.7346 x−40.848=0
x=−53.19 ,−8.92 ,15.64
The acceptable value is 15.64 years.
Hence, 15.64 year is the times for which the % of cigarette use by 8th graders would be 0%.
e. Local extreme values (maximum and minimum) is shown below:
Let f ( x ) =0.0055 x3 +0.2556 x2−2.7346 x−40.848
f ' ( x ) =0.0165 x2+0.51124 x−2.7346
f ' ( x )=0
0.0165 x2+ 0.51124 x−2.7346=0
x=−0.51124 ± √ 0.441849
0.033
Maximum ¿ −0.51124− √ 0.441849
0.033 =132.32
Minimum ¿ −0.51124+ √0.441849
0.033 =−47.48
Question 3
3

a. On examining the above data, it is apparent that the animals that are heavy in weight such as
elephant, hippopotamus and rhinoceros tend to have a lower relative speed in comparison to
deer, antelope and goat which are all light in weight. Hence based on the given data, it
seems that there is an inverse relationship between mass and relative speed. Also, it makes
sense that the relationship between the given variables is inversely proportional as the
amount of energy required to run at a given speed would be lesser for a lighter weighed
animal in comparison to a heavier counterpart.
b. Power regression model
y=98.309 x−0.493
c. Mass of a zebra x =?
Relative running speed y = 8.16 m/sec
y=98.309 x−0.493
8.16=98.309 x−0.493
x−0.493=0.083004
x=0.083004 ( 1
−0.493 )
x=155.78
4

Therefore, the mass of zebra is 155.78 kg whose relative running speed is 8.16 m/sec.
Question 4
The vertical asymptote equation is x=7 since at this value, the denominator in the function
becomes 0 and the function approaches a value of infinity.
Question 5
The horizontal asymptote equation is y=1 since in the given case, the degree of numerator and
denominator seem to be same.
Question 6
The required sketch is as indicated below.
5

Question 7
C ( t )= 5 t
0.01 t2 +3.3
t=¿ ( minutes )
C=Concentration of a drug ∈blood stream μg
ml
a. Maximum amount of drug in the body would be determined when C' ( t )=0
d
dt C ( t ) = d
dt ( 5 t
0.01 t2 +3.3 )
C' ( t )=5 ¿
C' ( t )=5 ¿
C' ( t )=5 ¿
C' ( t )=5 ¿
C' ( t )=0
Now,
5 ¿
−0.01 t2 +3.3=0
−0.01 t2 =−3.3
t2=330
tmax=18.17 Minutes (Maximum time)
Further,
Cmax would be the concentration at tmax .
C ( t )= 5 t
0.01 t2 +3.3
6

Cmax ( t ) = 5 tmax
0.01tmax
2 +3.3 = (5∗18.17)
0.01(18.17)2+ 3.3 =13.76
Hence, the maximum amount of drug in the body would be 13.76 μg
ml and the maximum time
would be 18.17 minutes.
b. It is apparent that the shape of the graph in the given context from t=0 to t =18.17 minutes is
exponential since there is surge in the concentration which tends to peak out by the 19th
minute. Clearly there is exponential trend especially at the beginning even though later the
trend is quite linear.
c. The slope from the maximum point to two hours after the drug indicates that there is a
gradual decay as the concentration of the drug tends to first decay at a faster pace and then
the pace of decay tends to slow down. The shape of this slope would be termed as broadly
logarithmic except the starting period when the slope is quite steep.
d. Equation of asymptotes C (t)
 Check for horizontal asymptotes
Here,
Degree of numerator = 1
Degree of denominator = 2
As the denominator’s degree is higher than the numerator’s degree then the horizontal
asymptotes is the x axis and y = 0.
Therefore, the equation of horizontal asymptotes is y = 0.
 Check for vertical asymptotes
Vertical asymptotes are undefined points and also the zeroes of the denominator.
As per the given function, 5t
0.01t2 +3.3, there is no undefined points. Therefore, no vertical
asymptotes.
7