Major Assignment: MAF101 Fundamentals of Finance - Trimester 1, 2019
VerifiedAdded on 2023/03/17
|14
|2639
|90
Homework Assignment
AI Summary
This assignment solution for MAF101, Fundamentals of Finance, covers several key financial concepts. Part 1 includes calculations for net present value, lump sum investments, bond pricing, and share valuation using the dividend growth model. Part 2 focuses on portfolio analysis, exploring the returns and risks associated with different investment strategies. It analyzes portfolio alpha, beta, and gamma, using historical data to assess risk and return profiles. The solution also addresses risk management principles, including diversifiable and non-diversifiable risks, the use of beta and standard deviation, and the implications of risk aversion. Finally, the assignment provides investment recommendations for different customer profiles based on their time horizons and risk tolerance.

Part 1
Question 1
Answer
The policy is not worth it.
The table below summarizes the policy cash inflows and outflows
Time Cash flow
1 $ 500.00
2 $ 600.00
3 $ 700.00
4 $ 800.00
5 $ 900.00
6 $ 1,100.00
65 $ (275,000.00)
Interest rate of 11% is applicable for time 1 to 6 and 7% is applicable for time 7 to 65
To determine if the policy worth buying or not, the Net Present Value of the cash flows should
be greater than zero.
The Net present value is calculated using the formula below:
NPV= Present value of cash inflows plus present value out outflows
NPV= ∑
i=1
6
CF t∗(1+11 %)−t + CF65*(1+7%)-65
The table below summarizes the present values of cash flows
Question 1
Answer
The policy is not worth it.
The table below summarizes the policy cash inflows and outflows
Time Cash flow
1 $ 500.00
2 $ 600.00
3 $ 700.00
4 $ 800.00
5 $ 900.00
6 $ 1,100.00
65 $ (275,000.00)
Interest rate of 11% is applicable for time 1 to 6 and 7% is applicable for time 7 to 65
To determine if the policy worth buying or not, the Net Present Value of the cash flows should
be greater than zero.
The Net present value is calculated using the formula below:
NPV= Present value of cash inflows plus present value out outflows
NPV= ∑
i=1
6
CF t∗(1+11 %)−t + CF65*(1+7%)-65
The table below summarizes the present values of cash flows
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
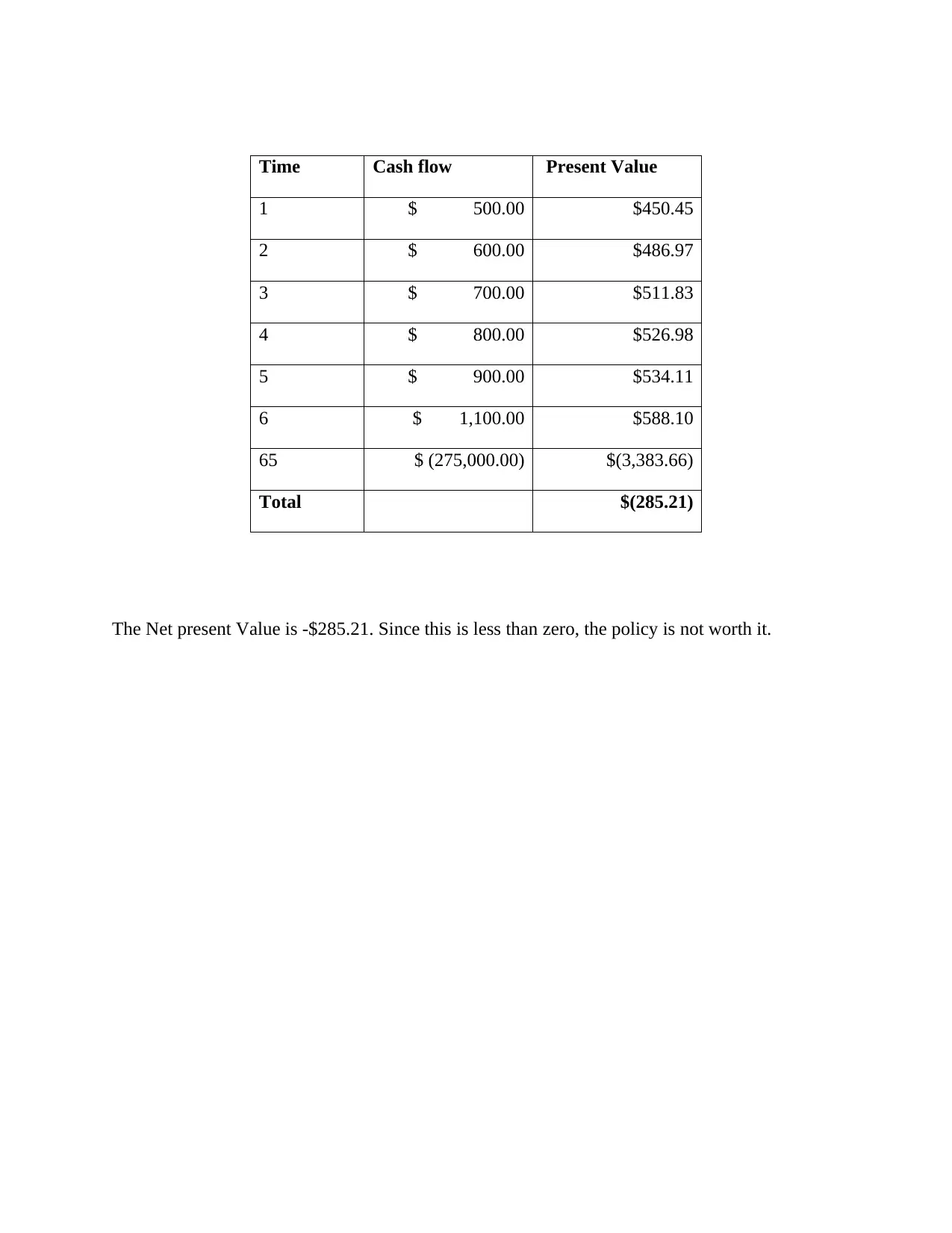
Time Cash flow Present Value
1 $ 500.00 $450.45
2 $ 600.00 $486.97
3 $ 700.00 $511.83
4 $ 800.00 $526.98
5 $ 900.00 $534.11
6 $ 1,100.00 $588.10
65 $ (275,000.00) $(3,383.66)
Total $(285.21)
The Net present Value is -$285.21. Since this is less than zero, the policy is not worth it.
1 $ 500.00 $450.45
2 $ 600.00 $486.97
3 $ 700.00 $511.83
4 $ 800.00 $526.98
5 $ 900.00 $534.11
6 $ 1,100.00 $588.10
65 $ (275,000.00) $(3,383.66)
Total $(285.21)
The Net present Value is -$285.21. Since this is less than zero, the policy is not worth it.

Question 2
Answer
A lump sum of $13,335.22 should be invested in B today.
To find the lump sum, we need to solve the equation:
Future Value of Investment B = Future Value of Investment A
Investment A
n =15-year annuity
PMT= $1,500
i(12) =interest rate of 8.7 percent compounded monthly
Investment B
n =15-year Lump sum
i(52) = interest 8 percent compounded weekly
Step 1: Find annual effective rate of interest, i for both investments
1+i = (1+ j
n)n (Madura, 2009)
Where i is the effective rate and j is the nominal rate of interest
Investment A
i = (1+i(12)/12)12 -1
=(1+0.087/12)^12-1
Answer
A lump sum of $13,335.22 should be invested in B today.
To find the lump sum, we need to solve the equation:
Future Value of Investment B = Future Value of Investment A
Investment A
n =15-year annuity
PMT= $1,500
i(12) =interest rate of 8.7 percent compounded monthly
Investment B
n =15-year Lump sum
i(52) = interest 8 percent compounded weekly
Step 1: Find annual effective rate of interest, i for both investments
1+i = (1+ j
n)n (Madura, 2009)
Where i is the effective rate and j is the nominal rate of interest
Investment A
i = (1+i(12)/12)12 -1
=(1+0.087/12)^12-1
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

=9.0554%
Investment B
i = (1+i(52)/52)52 -1
=(1+0.08/52)^52-1
=8.3220%
Step 2: Find Future Value of Investment A
Future Value of Annuity = PMT * [ (1+ i)15−1 ¿¿¿ i ]
= 1500 * [ (1+9.0554 %)15−1
9.0554 % ]
= $44,233.69
Step 3: Solve the equation: Future Value of Investment B = Future Value of Investment A
Future Value of Investment B= Future Value of Investment A
Lump sum*(1+8.3220%)15 =$44,233.69
Lump sum =44233.69/(1+8.3220%)15
Lump sum = $13,335.22
Investment B
i = (1+i(52)/52)52 -1
=(1+0.08/52)^52-1
=8.3220%
Step 2: Find Future Value of Investment A
Future Value of Annuity = PMT * [ (1+ i)15−1 ¿¿¿ i ]
= 1500 * [ (1+9.0554 %)15−1
9.0554 % ]
= $44,233.69
Step 3: Solve the equation: Future Value of Investment B = Future Value of Investment A
Future Value of Investment B= Future Value of Investment A
Lump sum*(1+8.3220%)15 =$44,233.69
Lump sum =44233.69/(1+8.3220%)15
Lump sum = $13,335.22
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
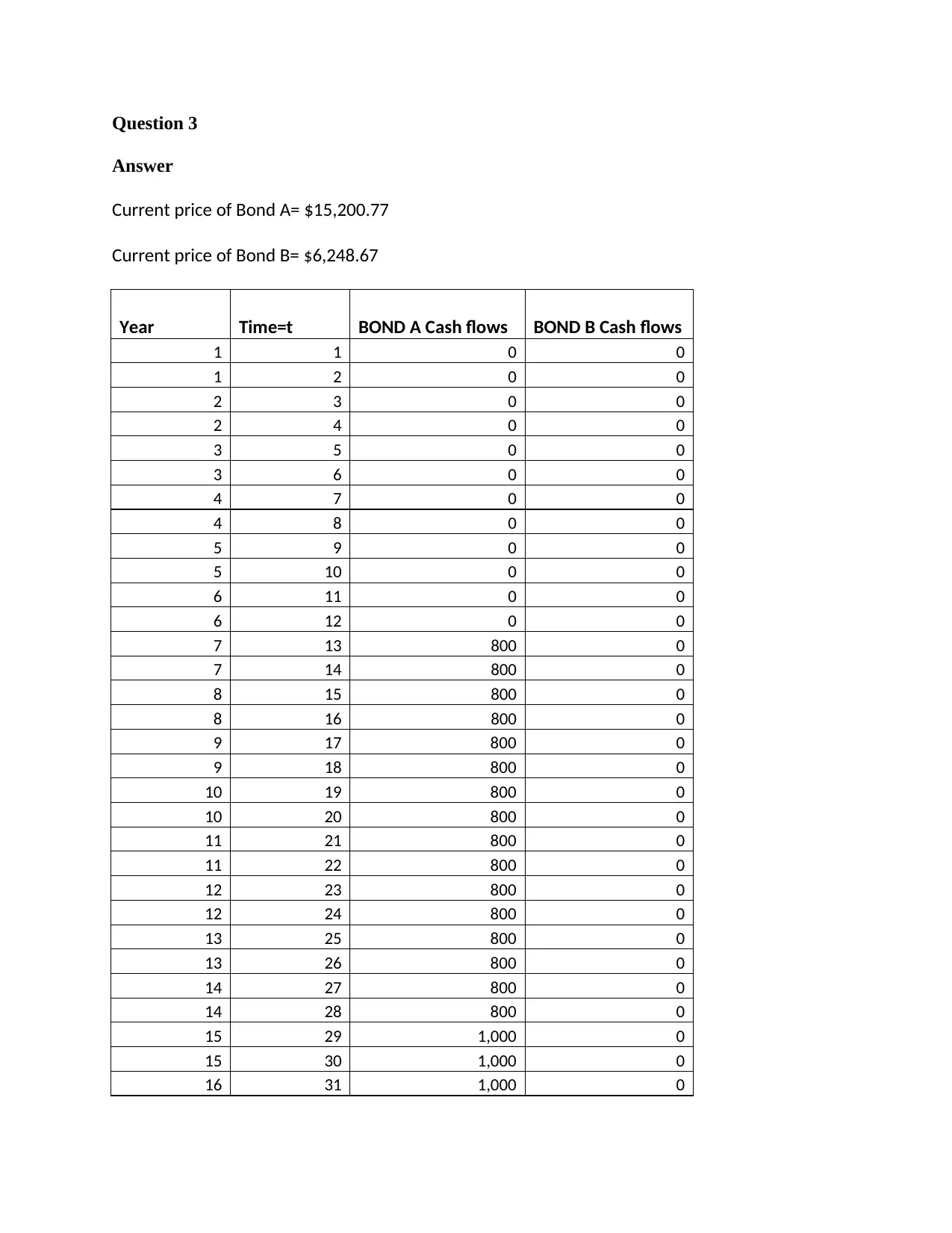
Question 3
Answer
Current price of Bond A= $15,200.77
Current price of Bond B= $6,248.67
Year Time=t BOND A Cash flows BOND B Cash flows
1 1 0 0
1 2 0 0
2 3 0 0
2 4 0 0
3 5 0 0
3 6 0 0
4 7 0 0
4 8 0 0
5 9 0 0
5 10 0 0
6 11 0 0
6 12 0 0
7 13 800 0
7 14 800 0
8 15 800 0
8 16 800 0
9 17 800 0
9 18 800 0
10 19 800 0
10 20 800 0
11 21 800 0
11 22 800 0
12 23 800 0
12 24 800 0
13 25 800 0
13 26 800 0
14 27 800 0
14 28 800 0
15 29 1,000 0
15 30 1,000 0
16 31 1,000 0
Answer
Current price of Bond A= $15,200.77
Current price of Bond B= $6,248.67
Year Time=t BOND A Cash flows BOND B Cash flows
1 1 0 0
1 2 0 0
2 3 0 0
2 4 0 0
3 5 0 0
3 6 0 0
4 7 0 0
4 8 0 0
5 9 0 0
5 10 0 0
6 11 0 0
6 12 0 0
7 13 800 0
7 14 800 0
8 15 800 0
8 16 800 0
9 17 800 0
9 18 800 0
10 19 800 0
10 20 800 0
11 21 800 0
11 22 800 0
12 23 800 0
12 24 800 0
13 25 800 0
13 26 800 0
14 27 800 0
14 28 800 0
15 29 1,000 0
15 30 1,000 0
16 31 1,000 0

16 32 1,000 0
17 33 1,000 0
17 34 1,000 0
18 35 1,000 0
18 36 1,000 0
19 37 1,000 0
19 38 1,000 0
20 39 1,000 0
20 40 31,000 30,000
Current price of Bond A
Face value = $30,000
n= 20 years.
PMT= $800 every six months for eight years after year 6, and finally pays $1,000 every six
months over the last six year
i(2)=8 percent compounded semiannually
Effective semiannual interest rate = i(2)/2= 4%
PV= 800 *[ 1−(1+4 %)−16 ¿¿¿ i ]∗(1+ 4 %)−12+ 1,000 * [ 1−(1+4 %)−12 ¿ ¿¿ i ]∗(1+ 4 % )−28+ ¿
30,000 * (1+4%)-40
= $15,200.77
Current price of Bond B
Face value =$30,000
n= 20 years
Nill coupon payments
17 33 1,000 0
17 34 1,000 0
18 35 1,000 0
18 36 1,000 0
19 37 1,000 0
19 38 1,000 0
20 39 1,000 0
20 40 31,000 30,000
Current price of Bond A
Face value = $30,000
n= 20 years.
PMT= $800 every six months for eight years after year 6, and finally pays $1,000 every six
months over the last six year
i(2)=8 percent compounded semiannually
Effective semiannual interest rate = i(2)/2= 4%
PV= 800 *[ 1−(1+4 %)−16 ¿¿¿ i ]∗(1+ 4 %)−12+ 1,000 * [ 1−(1+4 %)−12 ¿ ¿¿ i ]∗(1+ 4 % )−28+ ¿
30,000 * (1+4%)-40
= $15,200.77
Current price of Bond B
Face value =$30,000
n= 20 years
Nill coupon payments
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

PV =30,000*(1+4%)-20
= $6,248.67
= $6,248.67
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Question 4
The price of share can be determined using the Dividend growth model (Ro, 2015)
Present Value = D1/(k- g)
Where D1 = dividend paid for period, k = required return and g = growth factor (CF1, 2019).
D1= $1.95
K=11%
g=6%
Current price
PV = 1.95/(11%-6%)
=$39
Price in 3 years
=P0*(1+11%)3
=39*(1+11%)^3
=$53.34
The price of share can be determined using the Dividend growth model (Ro, 2015)
Present Value = D1/(k- g)
Where D1 = dividend paid for period, k = required return and g = growth factor (CF1, 2019).
D1= $1.95
K=11%
g=6%
Current price
PV = 1.95/(11%-6%)
=$39
Price in 3 years
=P0*(1+11%)3
=39*(1+11%)^3
=$53.34
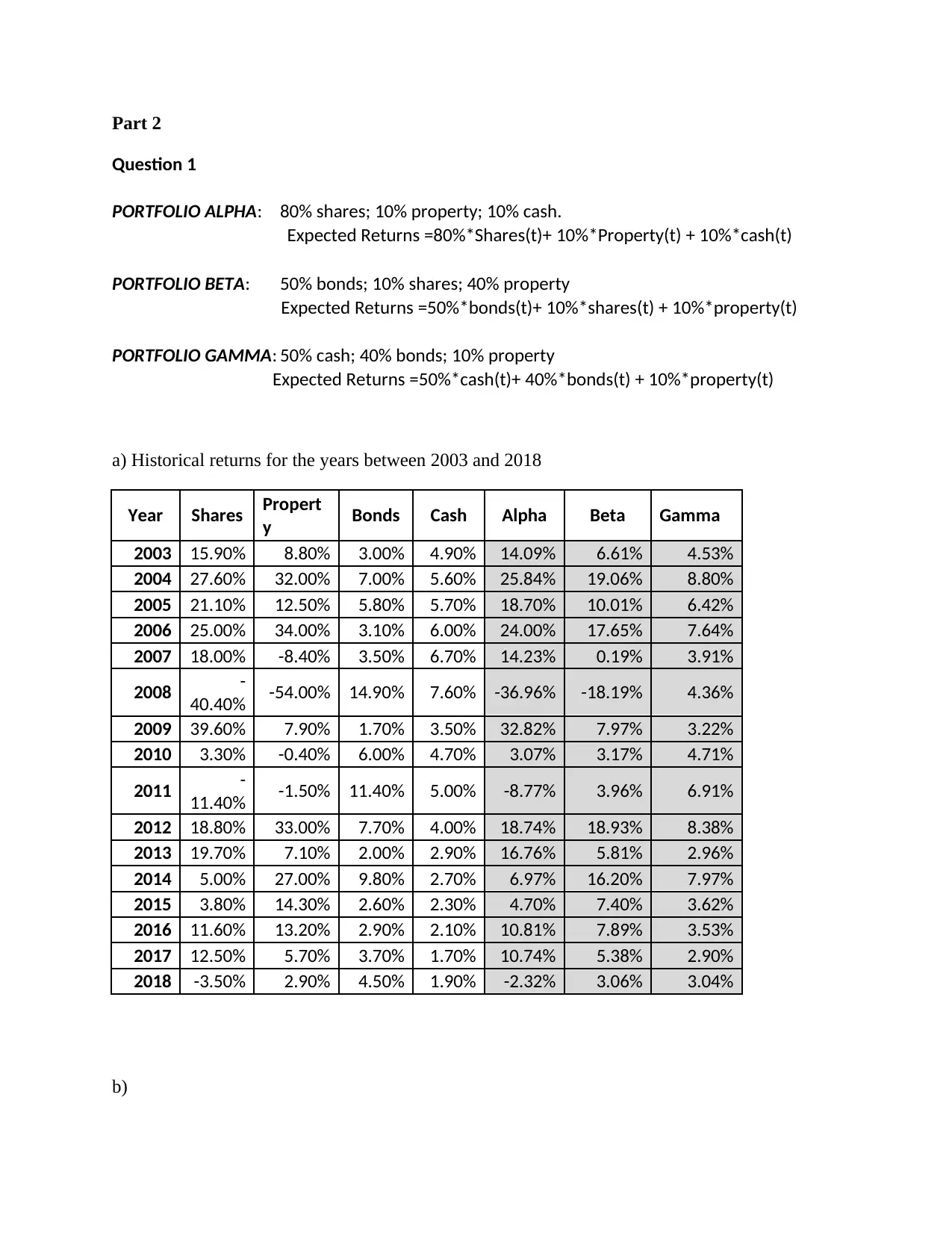
Part 2
Question 1
PORTFOLIO ALPHA: 80% shares; 10% property; 10% cash.
Expected Returns =80%*Shares(t)+ 10%*Property(t) + 10%*cash(t)
PORTFOLIO BETA: 50% bonds; 10% shares; 40% property
Expected Returns =50%*bonds(t)+ 10%*shares(t) + 10%*property(t)
PORTFOLIO GAMMA: 50% cash; 40% bonds; 10% property
Expected Returns =50%*cash(t)+ 40%*bonds(t) + 10%*property(t)
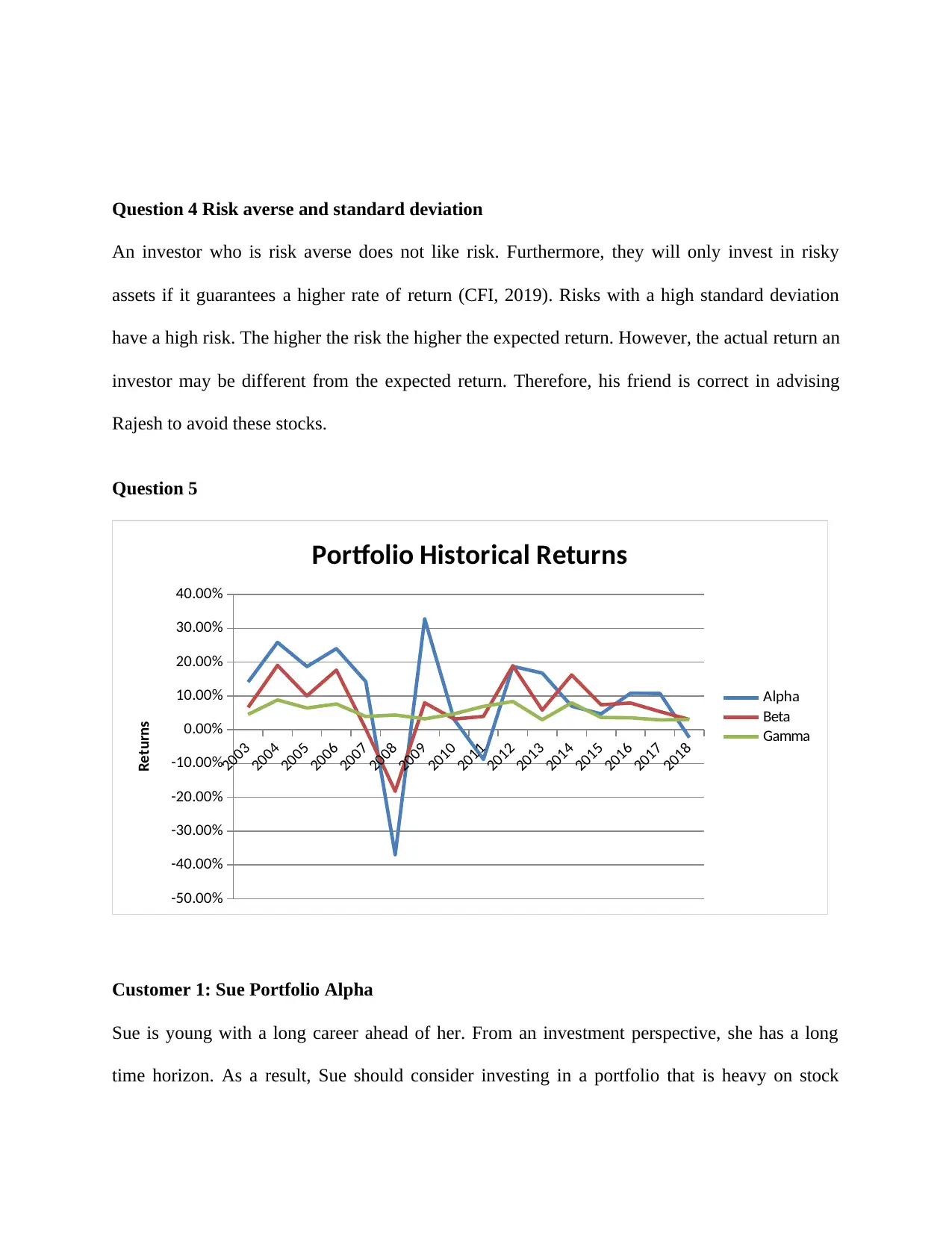
a) Historical returns for the years between 2003 and 2018
Year Shares Propert
y Bonds Cash Alpha Beta Gamma
2003 15.90% 8.80% 3.00% 4.90% 14.09% 6.61% 4.53%
2004 27.60% 32.00% 7.00% 5.60% 25.84% 19.06% 8.80%
2005 21.10% 12.50% 5.80% 5.70% 18.70% 10.01% 6.42%
2006 25.00% 34.00% 3.10% 6.00% 24.00% 17.65% 7.64%
2007 18.00% -8.40% 3.50% 6.70% 14.23% 0.19% 3.91%
2008 -
40.40% -54.00% 14.90% 7.60% -36.96% -18.19% 4.36%
2009 39.60% 7.90% 1.70% 3.50% 32.82% 7.97% 3.22%
2010 3.30% -0.40% 6.00% 4.70% 3.07% 3.17% 4.71%
2011 -
11.40% -1.50% 11.40% 5.00% -8.77% 3.96% 6.91%
2012 18.80% 33.00% 7.70% 4.00% 18.74% 18.93% 8.38%
2013 19.70% 7.10% 2.00% 2.90% 16.76% 5.81% 2.96%
2014 5.00% 27.00% 9.80% 2.70% 6.97% 16.20% 7.97%
2015 3.80% 14.30% 2.60% 2.30% 4.70% 7.40% 3.62%
2016 11.60% 13.20% 2.90% 2.10% 10.81% 7.89% 3.53%
2017 12.50% 5.70% 3.70% 1.70% 10.74% 5.38% 2.90%
2018 -3.50% 2.90% 4.50% 1.90% -2.32% 3.06% 3.04%
b)
Question 1
PORTFOLIO ALPHA: 80% shares; 10% property; 10% cash.
Expected Returns =80%*Shares(t)+ 10%*Property(t) + 10%*cash(t)
PORTFOLIO BETA: 50% bonds; 10% shares; 40% property
Expected Returns =50%*bonds(t)+ 10%*shares(t) + 10%*property(t)
PORTFOLIO GAMMA: 50% cash; 40% bonds; 10% property
Expected Returns =50%*cash(t)+ 40%*bonds(t) + 10%*property(t)
a) Historical returns for the years between 2003 and 2018
Year Shares Propert
y Bonds Cash Alpha Beta Gamma
2003 15.90% 8.80% 3.00% 4.90% 14.09% 6.61% 4.53%
2004 27.60% 32.00% 7.00% 5.60% 25.84% 19.06% 8.80%
2005 21.10% 12.50% 5.80% 5.70% 18.70% 10.01% 6.42%
2006 25.00% 34.00% 3.10% 6.00% 24.00% 17.65% 7.64%
2007 18.00% -8.40% 3.50% 6.70% 14.23% 0.19% 3.91%
2008 -
40.40% -54.00% 14.90% 7.60% -36.96% -18.19% 4.36%
2009 39.60% 7.90% 1.70% 3.50% 32.82% 7.97% 3.22%
2010 3.30% -0.40% 6.00% 4.70% 3.07% 3.17% 4.71%
2011 -
11.40% -1.50% 11.40% 5.00% -8.77% 3.96% 6.91%
2012 18.80% 33.00% 7.70% 4.00% 18.74% 18.93% 8.38%
2013 19.70% 7.10% 2.00% 2.90% 16.76% 5.81% 2.96%
2014 5.00% 27.00% 9.80% 2.70% 6.97% 16.20% 7.97%
2015 3.80% 14.30% 2.60% 2.30% 4.70% 7.40% 3.62%
2016 11.60% 13.20% 2.90% 2.10% 10.81% 7.89% 3.53%
2017 12.50% 5.70% 3.70% 1.70% 10.74% 5.38% 2.90%
2018 -3.50% 2.90% 4.50% 1.90% -2.32% 3.06% 3.04%
b)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
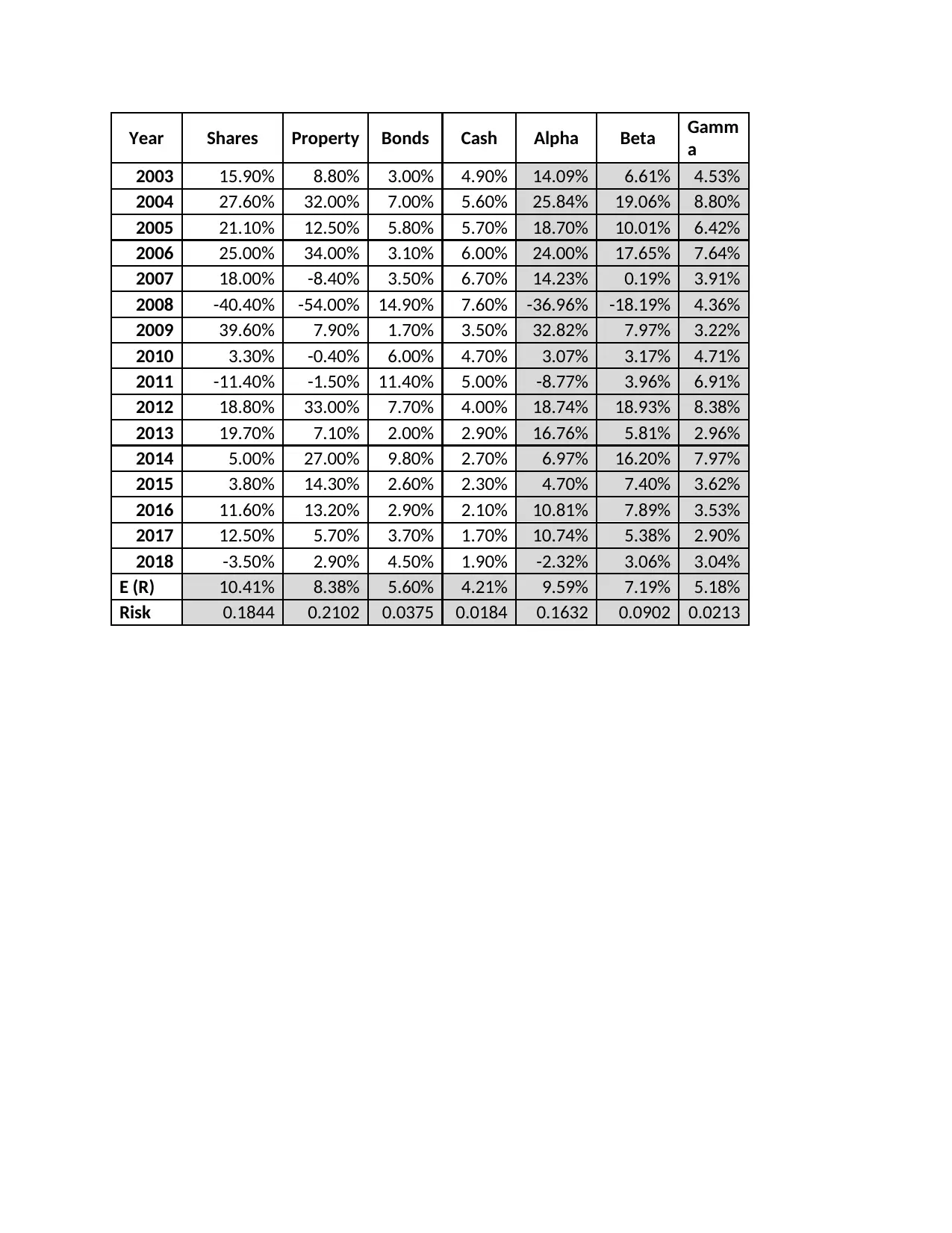
Year Shares Property Bonds Cash Alpha Beta Gamm
a
2003 15.90% 8.80% 3.00% 4.90% 14.09% 6.61% 4.53%
2004 27.60% 32.00% 7.00% 5.60% 25.84% 19.06% 8.80%
2005 21.10% 12.50% 5.80% 5.70% 18.70% 10.01% 6.42%
2006 25.00% 34.00% 3.10% 6.00% 24.00% 17.65% 7.64%
2007 18.00% -8.40% 3.50% 6.70% 14.23% 0.19% 3.91%
2008 -40.40% -54.00% 14.90% 7.60% -36.96% -18.19% 4.36%
2009 39.60% 7.90% 1.70% 3.50% 32.82% 7.97% 3.22%
2010 3.30% -0.40% 6.00% 4.70% 3.07% 3.17% 4.71%
2011 -11.40% -1.50% 11.40% 5.00% -8.77% 3.96% 6.91%
2012 18.80% 33.00% 7.70% 4.00% 18.74% 18.93% 8.38%
2013 19.70% 7.10% 2.00% 2.90% 16.76% 5.81% 2.96%
2014 5.00% 27.00% 9.80% 2.70% 6.97% 16.20% 7.97%
2015 3.80% 14.30% 2.60% 2.30% 4.70% 7.40% 3.62%
2016 11.60% 13.20% 2.90% 2.10% 10.81% 7.89% 3.53%
2017 12.50% 5.70% 3.70% 1.70% 10.74% 5.38% 2.90%
2018 -3.50% 2.90% 4.50% 1.90% -2.32% 3.06% 3.04%
E (R) 10.41% 8.38% 5.60% 4.21% 9.59% 7.19% 5.18%
Risk 0.1844 0.2102 0.0375 0.0184 0.1632 0.0902 0.0213
a
2003 15.90% 8.80% 3.00% 4.90% 14.09% 6.61% 4.53%
2004 27.60% 32.00% 7.00% 5.60% 25.84% 19.06% 8.80%
2005 21.10% 12.50% 5.80% 5.70% 18.70% 10.01% 6.42%
2006 25.00% 34.00% 3.10% 6.00% 24.00% 17.65% 7.64%
2007 18.00% -8.40% 3.50% 6.70% 14.23% 0.19% 3.91%
2008 -40.40% -54.00% 14.90% 7.60% -36.96% -18.19% 4.36%
2009 39.60% 7.90% 1.70% 3.50% 32.82% 7.97% 3.22%
2010 3.30% -0.40% 6.00% 4.70% 3.07% 3.17% 4.71%
2011 -11.40% -1.50% 11.40% 5.00% -8.77% 3.96% 6.91%
2012 18.80% 33.00% 7.70% 4.00% 18.74% 18.93% 8.38%
2013 19.70% 7.10% 2.00% 2.90% 16.76% 5.81% 2.96%
2014 5.00% 27.00% 9.80% 2.70% 6.97% 16.20% 7.97%
2015 3.80% 14.30% 2.60% 2.30% 4.70% 7.40% 3.62%
2016 11.60% 13.20% 2.90% 2.10% 10.81% 7.89% 3.53%
2017 12.50% 5.70% 3.70% 1.70% 10.74% 5.38% 2.90%
2018 -3.50% 2.90% 4.50% 1.90% -2.32% 3.06% 3.04%
E (R) 10.41% 8.38% 5.60% 4.21% 9.59% 7.19% 5.18%
Risk 0.1844 0.2102 0.0375 0.0184 0.1632 0.0902 0.0213
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Question 2
Diversifiable risk (also known as unsystematic risk) is unique to that asset. It can be eliminated
by investing in a portfolio with different assets whose returns are not correlated. Non-
diversifiable risk (also known as market or systematic risk) affects the entire market (Mitchell &
Mulherin, 1996). As a result, it cannot be diversified away by investing in multiple assets (Ben-
Horim & Levy, 1980).
Control of the risks
Indeed investors can control both the level of unsystematic risk and systematic risk in a portfolio.
For unsystematic, this is through diversification. For systematic, diversification will not work,
though options like hedging may control the risk (The Balance, 2018). However, controlling the
level of risk will be a costly effect on the portfolio’s estimated returns- the higher the risk the
higher the expected return (Inside Business, 2012).
Question 3- Beta and Standard deviation
The beta coefficient is a measure of a stock’s market risk, or the extent to which the returns on a
given stock move with the stock market. It measures the individual stocks volatility in
comparison to the entire market (Rosenberg & Guy, 1995). On the other hand, the standard
deviation measures the stock’s individual risk. Systematic risk cannot be removed no matter how
much an investor diversifies their assets. Therefore, using beta as a measure of risk is more
appropriate for a well-diversified as it takes market risk into consideration (Rosenberg & Guy,
1995).
Diversifiable risk (also known as unsystematic risk) is unique to that asset. It can be eliminated
by investing in a portfolio with different assets whose returns are not correlated. Non-
diversifiable risk (also known as market or systematic risk) affects the entire market (Mitchell &
Mulherin, 1996). As a result, it cannot be diversified away by investing in multiple assets (Ben-
Horim & Levy, 1980).
Control of the risks
Indeed investors can control both the level of unsystematic risk and systematic risk in a portfolio.
For unsystematic, this is through diversification. For systematic, diversification will not work,
though options like hedging may control the risk (The Balance, 2018). However, controlling the
level of risk will be a costly effect on the portfolio’s estimated returns- the higher the risk the
higher the expected return (Inside Business, 2012).
Question 3- Beta and Standard deviation
The beta coefficient is a measure of a stock’s market risk, or the extent to which the returns on a
given stock move with the stock market. It measures the individual stocks volatility in
comparison to the entire market (Rosenberg & Guy, 1995). On the other hand, the standard
deviation measures the stock’s individual risk. Systematic risk cannot be removed no matter how
much an investor diversifies their assets. Therefore, using beta as a measure of risk is more
appropriate for a well-diversified as it takes market risk into consideration (Rosenberg & Guy,
1995).
Question 4 Risk averse and standard deviation
An investor who is risk averse does not like risk. Furthermore, they will only invest in risky
assets if it guarantees a higher rate of return (CFI, 2019). Risks with a high standard deviation
have a high risk. The higher the risk the higher the expected return. However, the actual return an
investor may be different from the expected return. Therefore, his friend is correct in advising
Rajesh to avoid these stocks.
Question 5
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
2013
2014
2015
2016
2017
2018
-50.00%
-40.00%
-30.00%
-20.00%
-10.00%
0.00%
10.00%
20.00%
30.00%
40.00%
Portfolio Historical Returns
Alpha
Beta
Gamma
Returns
Customer 1: Sue Portfolio Alpha
Sue is young with a long career ahead of her. From an investment perspective, she has a long
time horizon. As a result, Sue should consider investing in a portfolio that is heavy on stock
An investor who is risk averse does not like risk. Furthermore, they will only invest in risky
assets if it guarantees a higher rate of return (CFI, 2019). Risks with a high standard deviation
have a high risk. The higher the risk the higher the expected return. However, the actual return an
investor may be different from the expected return. Therefore, his friend is correct in advising
Rajesh to avoid these stocks.
Question 5
2003
2004
2005
2006
2007
2008
2009
2010
2011
2012
2013
2014
2015
2016
2017
2018
-50.00%
-40.00%
-30.00%
-20.00%
-10.00%
0.00%
10.00%
20.00%
30.00%
40.00%
Portfolio Historical Returns
Alpha
Beta
Gamma
Returns
Customer 1: Sue Portfolio Alpha
Sue is young with a long career ahead of her. From an investment perspective, she has a long
time horizon. As a result, Sue should consider investing in a portfolio that is heavy on stock
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 14
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





