2018 Further Engineering Mathematics Assignment Solution
VerifiedAdded on 2023/06/10
|17
|2629
|468
Homework Assignment
AI Summary
This document presents a comprehensive solution to a Further Engineering Mathematics assignment. The solution includes detailed calculations and explanations for various mathematical concepts. Part (a) provides sketched graphs of trigonometric functions. Part (b) and (c) demonstrate the calculation of areas using double integrals. Part (d) involves the calculation of volume using a triple integral. Part (e) is not fully addressed in the provided text. Question 2 explores line integrals, curve lengths, and work done by a force. Question 3 utilizes the power method to find the dominant eigenvalue and eigenvector of a matrix. Question 4 applies the 2nd Runge-Kutta method to solve an initial value problem. Finally, Question 5 analyzes a periodic function using Fourier series, including sketching and coefficient calculations.

2018
INSTITUTIONAL AFFILIATION
FACULTY OR DEPARTMENT
COURSE ID & NAME
TITLE:
FUTURE ENGINEERING MATHEMATICS
STUDENT NAME
STUDENT ID NUMBER
PROFESSOR (TUTOR)
DATE OF SUBMISSION
INSTITUTIONAL AFFILIATION
FACULTY OR DEPARTMENT
COURSE ID & NAME
TITLE:
FUTURE ENGINEERING MATHEMATICS
STUDENT NAME
STUDENT ID NUMBER
PROFESSOR (TUTOR)
DATE OF SUBMISSION
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
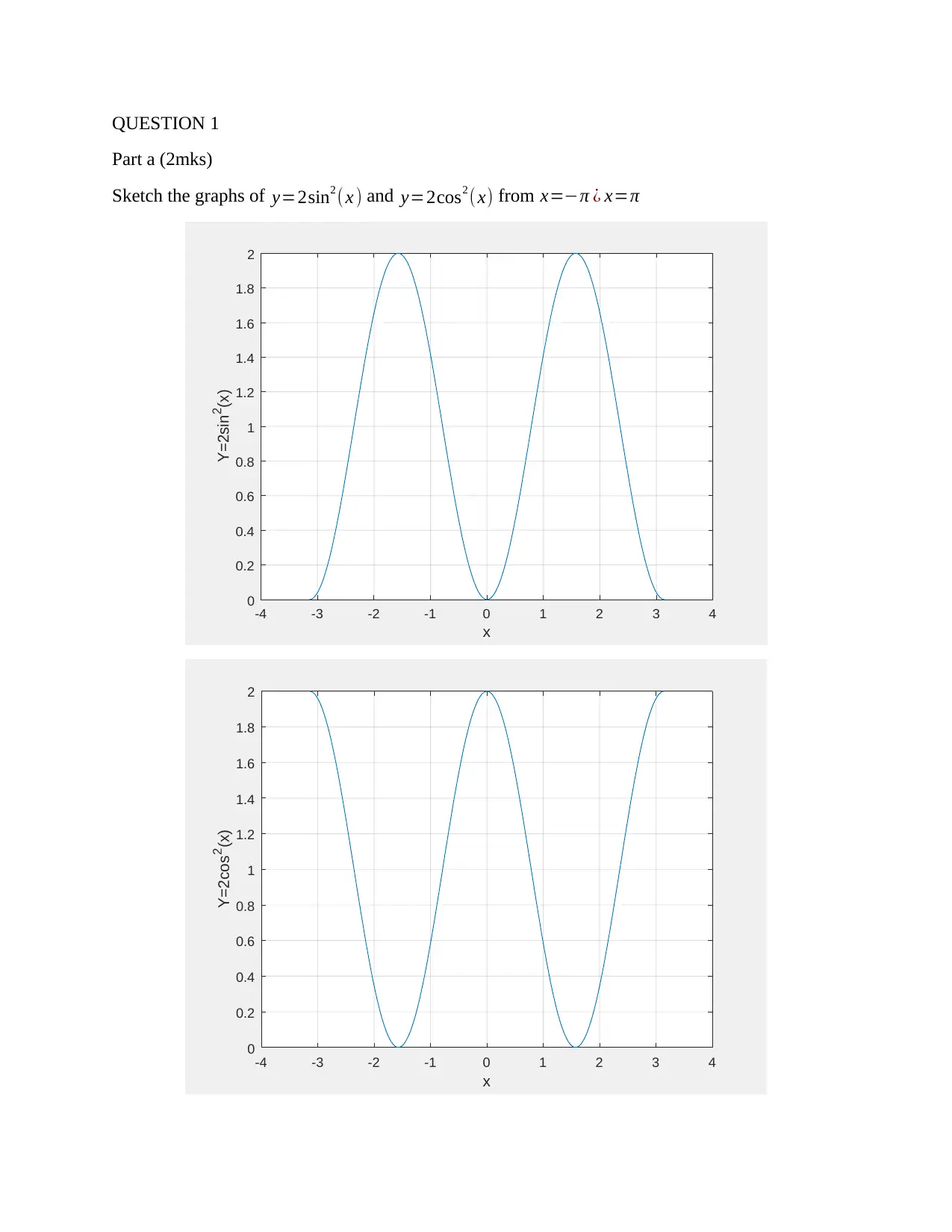
QUESTION 1
Part a (2mks)
Sketch the graphs of y=2sin2 ( x ) and y=2cos2 (x) from x=−π ¿ x=π
-4 -3 -2 -1 0 1 2 3 4
x
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
Y=2sin 2 (x)
-4 -3 -2 -1 0 1 2 3 4
x
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
Y=2cos2(x)
Part a (2mks)
Sketch the graphs of y=2sin2 ( x ) and y=2cos2 (x) from x=−π ¿ x=π
-4 -3 -2 -1 0 1 2 3 4
x
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
Y=2sin 2 (x)
-4 -3 -2 -1 0 1 2 3 4
x
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
Y=2cos2(x)
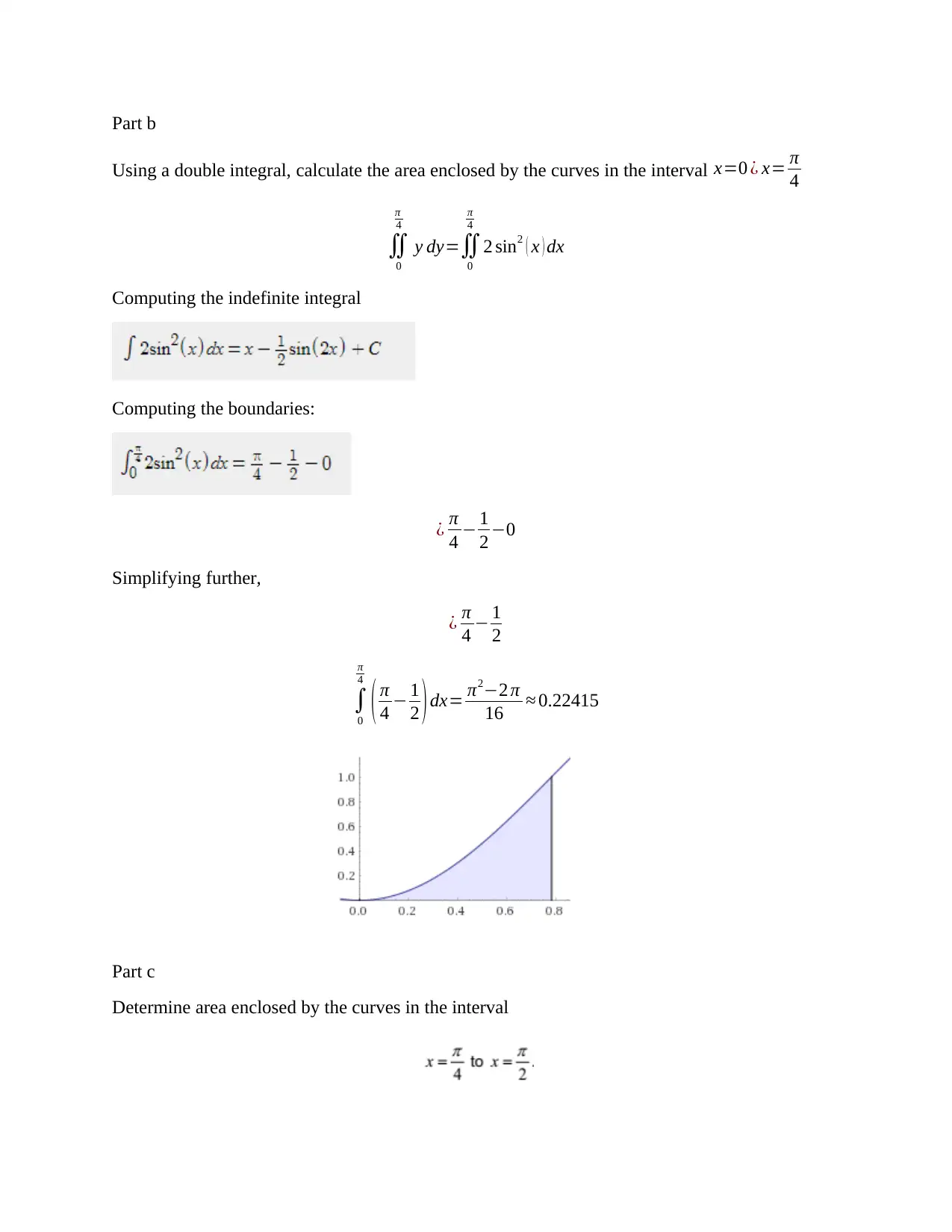
Part b
Using a double integral, calculate the area enclosed by the curves in the interval x=0 ¿ x= π
4
∬
0
π
4
y dy=∬
0
π
4
2 sin2 ( x ) dx
Computing the indefinite integral
Computing the boundaries:
¿ π
4 − 1
2 −0
Simplifying further,
¿ π
4 − 1
2
∫
0
π
4
( π
4 − 1
2 )dx= π2−2 π
16 ≈ 0.22415
Part c
Determine area enclosed by the curves in the interval
Using a double integral, calculate the area enclosed by the curves in the interval x=0 ¿ x= π
4
∬
0
π
4
y dy=∬
0
π
4
2 sin2 ( x ) dx
Computing the indefinite integral
Computing the boundaries:
¿ π
4 − 1
2 −0
Simplifying further,
¿ π
4 − 1
2
∫
0
π
4
( π
4 − 1
2 )dx= π2−2 π
16 ≈ 0.22415
Part c
Determine area enclosed by the curves in the interval
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
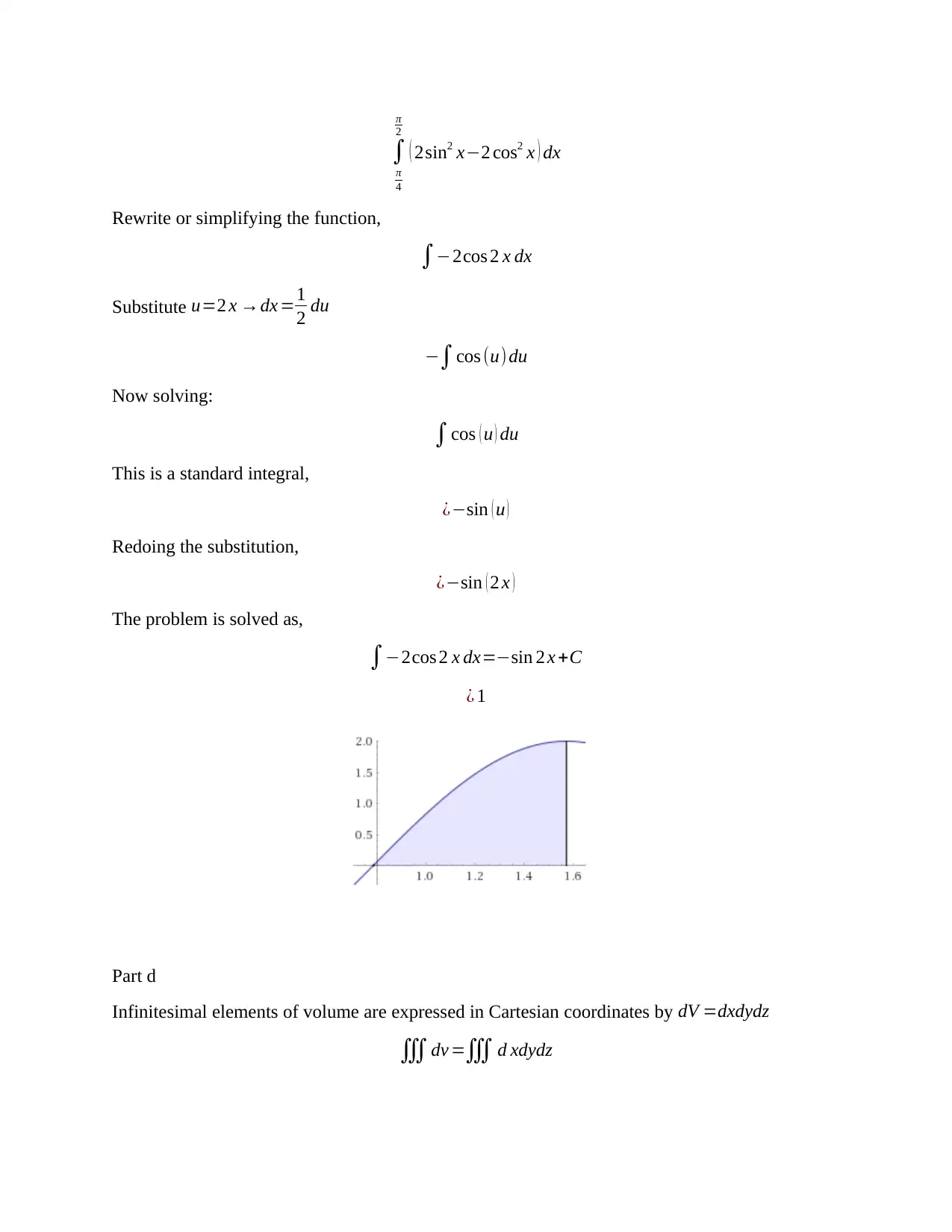
∫
π
4
π
2
( 2sin2 x−2 cos2 x ) dx
Rewrite or simplifying the function,
∫−2cos 2 x dx
Substitute u=2 x →dx =1
2 du
−∫cos (u) du
Now solving:
∫cos ( u ) du
This is a standard integral,
¿−sin ( u )
Redoing the substitution,
¿−sin ( 2 x )
The problem is solved as,
∫−2cos 2 x dx=−sin 2 x +C
¿ 1
Part d
Infinitesimal elements of volume are expressed in Cartesian coordinates by dV =dxdydz
∭dv =∭ d xdydz
π
4
π
2
( 2sin2 x−2 cos2 x ) dx
Rewrite or simplifying the function,
∫−2cos 2 x dx
Substitute u=2 x →dx =1
2 du
−∫cos (u) du
Now solving:
∫cos ( u ) du
This is a standard integral,
¿−sin ( u )
Redoing the substitution,
¿−sin ( 2 x )
The problem is solved as,
∫−2cos 2 x dx=−sin 2 x +C
¿ 1
Part d
Infinitesimal elements of volume are expressed in Cartesian coordinates by dV =dxdydz
∭dv =∭ d xdydz
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

¿∫
0
3 x
∫
2.5
2.5
∫
ex
❑
dv
Part e
Infinitesimal elements of volume are expressed in spherical polar coordinates as
dV =r2 sin (θ) drd θ d φ
QUESTION 2
Part a
Evaluate I=∫
c
❑
( 2 xy + y ) dxalong the path C described parametrically by x=t2 , y= 1
t2 ¿ t=C ¿ 4
Solution
0
3 x
∫
2.5
2.5
∫
ex
❑
dv
Part e
Infinitesimal elements of volume are expressed in spherical polar coordinates as
dV =r2 sin (θ) drd θ d φ
QUESTION 2
Part a
Evaluate I=∫
c
❑
( 2 xy + y ) dxalong the path C described parametrically by x=t2 , y= 1
t2 ¿ t=C ¿ 4
Solution

¿∨⃗ r ( t ) ∨¿= √ ( dx
dt )2
+ ( dy
dt )2
I =∫
c
❑
( 2t2 . 1
t2 + 1
t2 )||⃗r ( t )||dt
dx
dt =2t , dy
dt =−2
t3
||⃗r ( t )||= √ ( 2t ) 2+ ( −2
t3 )
2
= √ 4 t2+ 4
t6
||⃗r ( t )||=2 ( √ 1+t8
t6 )
I =∫
c
4
( 2+ 1
t2 )∗2 ( √ 1+t8
t6 ) dt
The line integral is given as,
I =∫
c
4
2 ( 2+ 1
t2 ) ( √ 1+t8
t6 ) dt
Part b
Calculate the length of the curve, y=ln |sec ( x )|from x=0 ¿ x= π
3
y=ln |sec ( x )|0 ≤ x ≤ π
3
For the given interval,
|sec ( x )|=sec ( x )
y' = 1
sec ( x ) ( sec x )'=sec x ( tan x
sec x )=tan x
length=∫ √ ( 1+ ( y' ) 2
) dx
y=ln |sec x|∧x=0¿ x= π
3
¿∫ √1+tan2 x dx for thelimits
dt )2
+ ( dy
dt )2
I =∫
c
❑
( 2t2 . 1
t2 + 1
t2 )||⃗r ( t )||dt
dx
dt =2t , dy
dt =−2
t3
||⃗r ( t )||= √ ( 2t ) 2+ ( −2
t3 )
2
= √ 4 t2+ 4
t6
||⃗r ( t )||=2 ( √ 1+t8
t6 )
I =∫
c
4
( 2+ 1
t2 )∗2 ( √ 1+t8
t6 ) dt
The line integral is given as,
I =∫
c
4
2 ( 2+ 1
t2 ) ( √ 1+t8
t6 ) dt
Part b
Calculate the length of the curve, y=ln |sec ( x )|from x=0 ¿ x= π
3
y=ln |sec ( x )|0 ≤ x ≤ π
3
For the given interval,
|sec ( x )|=sec ( x )
y' = 1
sec ( x ) ( sec x )'=sec x ( tan x
sec x )=tan x
length=∫ √ ( 1+ ( y' ) 2
) dx
y=ln |sec x|∧x=0¿ x= π
3
¿∫ √1+tan2 x dx for thelimits
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

¿∫ sec x dx for thelimita
¿ [ ln ( sec x + tan x ) ] , between x=0 ¿ x= π
3
¿ ln ( sec ( π
3 ) + tan ( π
3 ))
sec ( π
3 )= √ 1+ tan2 π
3 = √ 1+3=2
¿ ln ( 2+1 )=ln ( 3 )=1.09
Part c
Find the work done by the force F= ( 3 xy +4 ) i+ y3 j moving anticlockwise around the boundaries
of the triangle defined by the points (0,0), (4,0), and (4,4).
SOLUTION
Denoting the points as C1, C2, and C3.
C1= ( 0,0 ) C2 = ( 4,4 ) C3= ( 4,0 )
Dealing with the line segments
C= ( 0,0 ) ¿ ( 4,4 )∧ ( 4,4 ) ¿ ( 4,0 )∧ ( 4,0 ) ¿ ( 0,0 )
∫
∁
❑
fds=∫
C1
❑
fds+∫
C2
❑
fds+∫
C3
❑
fds
F= ( 3 xy +4 ) i+ y3 j
∇ f = ( 3 xy+ 4 , y3 ) =F
f x=3 y
f y=3 x ,3 y2
c1= {x=0. ( 1−t ) +2 t
y=0. ( 1−t ) +t }
c2= {x=4 . ( 1−t )+ 2t
y =4 . ( 1−t ) +t }
c3= {x=4 . ( 1−t )+ 2t
y=0. ( 1−t ) +t }
¿ [ ln ( sec x + tan x ) ] , between x=0 ¿ x= π
3
¿ ln ( sec ( π
3 ) + tan ( π
3 ))
sec ( π
3 )= √ 1+ tan2 π
3 = √ 1+3=2
¿ ln ( 2+1 )=ln ( 3 )=1.09
Part c
Find the work done by the force F= ( 3 xy +4 ) i+ y3 j moving anticlockwise around the boundaries
of the triangle defined by the points (0,0), (4,0), and (4,4).
SOLUTION
Denoting the points as C1, C2, and C3.
C1= ( 0,0 ) C2 = ( 4,4 ) C3= ( 4,0 )
Dealing with the line segments
C= ( 0,0 ) ¿ ( 4,4 )∧ ( 4,4 ) ¿ ( 4,0 )∧ ( 4,0 ) ¿ ( 0,0 )
∫
∁
❑
fds=∫
C1
❑
fds+∫
C2
❑
fds+∫
C3
❑
fds
F= ( 3 xy +4 ) i+ y3 j
∇ f = ( 3 xy+ 4 , y3 ) =F
f x=3 y
f y=3 x ,3 y2
c1= {x=0. ( 1−t ) +2 t
y=0. ( 1−t ) +t }
c2= {x=4 . ( 1−t )+ 2t
y =4 . ( 1−t ) +t }
c3= {x=4 . ( 1−t )+ 2t
y=0. ( 1−t ) +t }
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

∫
∁
❑
fds=∫
0,0
4,4
❑+∫
4,4
4,0
fds+∫
4,0
0,0
fds
The gradient vector field is,
¿ 3 √ 5∫ ( 4 t2−t2 ) √ 5 dt +∫ ( 2−t2 ) − ( t +1 ) 2 √ 2 dt+∫ ( 1−t ) 2−4 ¿ ¿
¿ 3 √ 5∫
0
1
t2 dt + √ 2∫
0
1
( 3−6 t ) dt+ √ 5∫
0
1
(−3+6 t=3 t2 ) dt
¿ 6
Part d
By using Green’s Theorem, verify this result with a double integral over the area of the triangle.
¿∫
0
4
( 14+10 t ) dt=6
QUESTION 3
Use the power method to find, correct to 3 decimal places, the dominant eigenvalue, and a
corresponding eigenvector of the matrix.
[ 0 11 −5
−2 17 −7
−4 −26 −10 ]T
Start with the initial vector [1,1,1]T and work to 3 decimal places throughout.
∁
❑
fds=∫
0,0
4,4
❑+∫
4,4
4,0
fds+∫
4,0
0,0
fds
The gradient vector field is,
¿ 3 √ 5∫ ( 4 t2−t2 ) √ 5 dt +∫ ( 2−t2 ) − ( t +1 ) 2 √ 2 dt+∫ ( 1−t ) 2−4 ¿ ¿
¿ 3 √ 5∫
0
1
t2 dt + √ 2∫
0
1
( 3−6 t ) dt+ √ 5∫
0
1
(−3+6 t=3 t2 ) dt
¿ 6
Part d
By using Green’s Theorem, verify this result with a double integral over the area of the triangle.
¿∫
0
4
( 14+10 t ) dt=6
QUESTION 3
Use the power method to find, correct to 3 decimal places, the dominant eigenvalue, and a
corresponding eigenvector of the matrix.
[ 0 11 −5
−2 17 −7
−4 −26 −10 ]T
Start with the initial vector [1,1,1]T and work to 3 decimal places throughout.

AT = [ 0 11 −5
−2 17 −7
−4 −26 −10 ]T
A=
[ 0 −2 −4
11 17 −26
−5 −7 −10 ]T
initial approximations , x0= [ 1
1
1 ] ,
Taking out the largest element of the resultant matrix,
x1= A ~x1=
( 0 −2 −4
11 17 −26
−5 −7 −10 )(1
1
1 )= ( −6
2
−22 )=−22 ( 0.2727
−0.0909
1.0000 )
Using the resulting matrix as the new initial vector for the next iteration,
x2= A ~x2=
( 0 −2 −4
11 17 −26
−5 −7 −10 )( 0.2727
−0.0909
1.0000 )=
( −3.8182
−24.5456
−10.7272 )=−24.5456 (0.1556
1.000
0.4370 )
Repeating the same procedure to obtain an iteration of the sequence,
x3= A ~x3=
( 0 −2 −4
11 17 −26
−5 −7 −10 )(0.1556
1.000
0.4370 )=
( −3.7481
7.3483
−12.1481 )=−12.1481 ( 0.3085
−0.6049
1.000 )
x3= A ~x3=
( 0 −2 −4
11 17 −26
−5 −7 −10 )( 0.3085
−0.6049
1.0000 )=
( −2.7902
−32.8893
−7.3084 )=−32.8893 (0.0848
1.000
0.2222 )
x4 =A ~x4 =
( 0 −2 −4
11 17 −26
−5 −7 −10 )(0.0848
1.000
0.2222 )=
(−2.8888
12.1556
−9.6463 )=12.1556 (−0.2377
1.000
−0.7936 )
x4 =A ~x4 =
( 0 −2 −4
11 17 −26
−5 −7 −10 )(−0.2377
1.000
−0.7936 )=
( 1.1743
35.0186
2.1239 )=35.0186 (0.0335
1.000
0.0607 )
x5= A ~x5=
( 0 −2 −4
11 17 −26
−5 −7 −10 )(0.0335
1.000
0.0607 )=
(−2.2426
15.7919
−7.7742 )=15.7919 (−0.1420
1.000
−0.4923 )
−2 17 −7
−4 −26 −10 ]T
A=
[ 0 −2 −4
11 17 −26
−5 −7 −10 ]T
initial approximations , x0= [ 1
1
1 ] ,
Taking out the largest element of the resultant matrix,
x1= A ~x1=
( 0 −2 −4
11 17 −26
−5 −7 −10 )(1
1
1 )= ( −6
2
−22 )=−22 ( 0.2727
−0.0909
1.0000 )
Using the resulting matrix as the new initial vector for the next iteration,
x2= A ~x2=
( 0 −2 −4
11 17 −26
−5 −7 −10 )( 0.2727
−0.0909
1.0000 )=
( −3.8182
−24.5456
−10.7272 )=−24.5456 (0.1556
1.000
0.4370 )
Repeating the same procedure to obtain an iteration of the sequence,
x3= A ~x3=
( 0 −2 −4
11 17 −26
−5 −7 −10 )(0.1556
1.000
0.4370 )=
( −3.7481
7.3483
−12.1481 )=−12.1481 ( 0.3085
−0.6049
1.000 )
x3= A ~x3=
( 0 −2 −4
11 17 −26
−5 −7 −10 )( 0.3085
−0.6049
1.0000 )=
( −2.7902
−32.8893
−7.3084 )=−32.8893 (0.0848
1.000
0.2222 )
x4 =A ~x4 =
( 0 −2 −4
11 17 −26
−5 −7 −10 )(0.0848
1.000
0.2222 )=
(−2.8888
12.1556
−9.6463 )=12.1556 (−0.2377
1.000
−0.7936 )
x4 =A ~x4 =
( 0 −2 −4
11 17 −26
−5 −7 −10 )(−0.2377
1.000
−0.7936 )=
( 1.1743
35.0186
2.1239 )=35.0186 (0.0335
1.000
0.0607 )
x5= A ~x5=
( 0 −2 −4
11 17 −26
−5 −7 −10 )(0.0335
1.000
0.0607 )=
(−2.2426
15.7919
−7.7742 )=15.7919 (−0.1420
1.000
−0.4923 )
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

x6= A ~x6= ( 0 −2 −4
11 17 −26
−5 −7 −10)(−0.1420
1.000
−0.4923 )= (−0.0308
28.2374
−1.3671 )=28.2374 (−0.0011
1.0000
−0.0484 )
x7= A ~x7= ( 0 −2 −4
11 17 −26
−5 −7 −10 )( −0.0011
1.0000
−0.0484 )= (
−1.8063
18.2468
−6.5104 ) =18.2468 (
−0.0990
1.0000
−0.3568 )
x8= A ~x8= ( 0 −2 −4
11 17 −26
−5 −7 −10)(−0.0990
1.0000
−0.3568 )= (−0.5728
25.1878
−2.9370 )=25.1878 (−0.0227
1.0000
−0.1166 )
x9= A ~x9= ( 0 −2 −4
11 17 −26
−5 −7 −10)(
−0.0227
1.0000
−0.1166 )= (
−1.5336
19.7816
−5.7203 )=19.7816 (
−0.0775
1.0000
−0.2892 )
x10= A ~x10=
( 0 −2 −4
11 17 −26
−5 −7 −10 )(−0.0775
1.0000
−0.2892 )= (−0.8433
23.6656
−3.7207 )=23.6656 (−0.0356
1.0000
−0.1572 )
To obtain the eigen values and dominant eigen vector, the iterations are carried out
progressively. The dominant eigenvector is obtained as,
23.6656 … . dominant eigen value
(−0.0356
1.0000
−0.1572 )=dominant eigenvector
QUESTION 4
Consider the initial value problem,
dv
dt =10−0.1 v with vo =50 at to=0
Using the 2nd Runge-Kutta method to calculate the approximate value of v at t=0.4, using step
size h=0.2 and working to six significant figures.
The modified Euler’s method is the second-order Runge Kutta method,
11 17 −26
−5 −7 −10)(−0.1420
1.000
−0.4923 )= (−0.0308
28.2374
−1.3671 )=28.2374 (−0.0011
1.0000
−0.0484 )
x7= A ~x7= ( 0 −2 −4
11 17 −26
−5 −7 −10 )( −0.0011
1.0000
−0.0484 )= (
−1.8063
18.2468
−6.5104 ) =18.2468 (
−0.0990
1.0000
−0.3568 )
x8= A ~x8= ( 0 −2 −4
11 17 −26
−5 −7 −10)(−0.0990
1.0000
−0.3568 )= (−0.5728
25.1878
−2.9370 )=25.1878 (−0.0227
1.0000
−0.1166 )
x9= A ~x9= ( 0 −2 −4
11 17 −26
−5 −7 −10)(
−0.0227
1.0000
−0.1166 )= (
−1.5336
19.7816
−5.7203 )=19.7816 (
−0.0775
1.0000
−0.2892 )
x10= A ~x10=
( 0 −2 −4
11 17 −26
−5 −7 −10 )(−0.0775
1.0000
−0.2892 )= (−0.8433
23.6656
−3.7207 )=23.6656 (−0.0356
1.0000
−0.1572 )
To obtain the eigen values and dominant eigen vector, the iterations are carried out
progressively. The dominant eigenvector is obtained as,
23.6656 … . dominant eigen value
(−0.0356
1.0000
−0.1572 )=dominant eigenvector
QUESTION 4
Consider the initial value problem,
dv
dt =10−0.1 v with vo =50 at to=0
Using the 2nd Runge-Kutta method to calculate the approximate value of v at t=0.4, using step
size h=0.2 and working to six significant figures.
The modified Euler’s method is the second-order Runge Kutta method,
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

X n+1=X n+ ∆ t
2 [ f ( xn ,tn ) + f ( xn+∆ tf ( xn ,tn ) , tn + ∆t ) ]
xi+1
¿ =xi−∆ t xi
2
To solve the ode using 2nd order RK method,
Initialization,
k =0 , h= b−t0
n y ( tk ) = yk
Predict the solution,
yk +1= yk + hf ( tk +1 , yk +1 , p )
2
Increment the value,
tk+1=tk +h , k =k +1
Using the algorithm to find the solution,
dv
dt =10−0.1 v , , v0 =50 at t0=0 h=0.2
Step 1:
V i+ 1=vi + f ( ti , vi ) h
vi =50+f ( 0,50 ) 0.2
¿ 50+ ( 10−0.1∗50 ) 0.2
¿ 50+ ( 5 ) 0.2
vi =51
Step 2:
v2=v1 +f ( t1 , v1 ) h
¿ 51+ ( 10−0.1∗51 ) 0.2
2 [ f ( xn ,tn ) + f ( xn+∆ tf ( xn ,tn ) , tn + ∆t ) ]
xi+1
¿ =xi−∆ t xi
2
To solve the ode using 2nd order RK method,
Initialization,
k =0 , h= b−t0
n y ( tk ) = yk
Predict the solution,
yk +1= yk + hf ( tk +1 , yk +1 , p )
2
Increment the value,
tk+1=tk +h , k =k +1
Using the algorithm to find the solution,
dv
dt =10−0.1 v , , v0 =50 at t0=0 h=0.2
Step 1:
V i+ 1=vi + f ( ti , vi ) h
vi =50+f ( 0,50 ) 0.2
¿ 50+ ( 10−0.1∗50 ) 0.2
¿ 50+ ( 5 ) 0.2
vi =51
Step 2:
v2=v1 +f ( t1 , v1 ) h
¿ 51+ ( 10−0.1∗51 ) 0.2
¿ 51+ ( 0.98 )
v2=51.98 , at t=0.2 , h=0.2
Step 3:
v3 =v2 +f ( t2 , v2 ) h
¿ 51.98+ ( 10−0.1∗51.98 ) 0.2
v2=52.9404 at t=0.4 , h=0.2
¿ 52.9404 ¿ 6 significant figures
QUESTION 5
The periodic function has a period 2pi. It is defined in the interval 0 ≤ x ≤ π by
f ( x )=x2
(a) Sketching the function on the interval for two cases,
A function is an even function when f ( −x ) =f (x )
-10 -8 -6 -4 -2 0 2 4 6 8
0
10
20
30
40
50
60
70
80
90
A function is said to be odd function when f ( −x ) =−f ( x)
v2=51.98 , at t=0.2 , h=0.2
Step 3:
v3 =v2 +f ( t2 , v2 ) h
¿ 51.98+ ( 10−0.1∗51.98 ) 0.2
v2=52.9404 at t=0.4 , h=0.2
¿ 52.9404 ¿ 6 significant figures
QUESTION 5
The periodic function has a period 2pi. It is defined in the interval 0 ≤ x ≤ π by
f ( x )=x2
(a) Sketching the function on the interval for two cases,
A function is an even function when f ( −x ) =f (x )
-10 -8 -6 -4 -2 0 2 4 6 8
0
10
20
30
40
50
60
70
80
90
A function is said to be odd function when f ( −x ) =−f ( x)
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 17
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.




