Capital Budgeting: Cost of Equity, NPV, IRR, and MIRR Solutions
VerifiedAdded on 2022/09/06
|9
|1291
|22
Homework Assignment
AI Summary
This document provides a comprehensive set of solutions for a capital budgeting assignment. The solutions cover various aspects of financial analysis and investment project evaluation. The document begins by calculating the cost of equity using the Capital Asset Pricing Model (CAPM). It then proceeds to analyze a project using Net Present Value (NPV), Internal Rate of Return (IRR), Modified Internal Rate of Return (MIRR), Profitability Index (PI), Payback Period, and Discounted Payback Period. The assignment also includes a comparative analysis of two projects, calculating NPV and IRR at different discount rates for each. The analysis includes formulas and step-by-step calculations to illustrate each concept. The document provides a clear understanding of capital budgeting techniques and their application in financial decision-making.

1
Capital Budgeting
Capital Budgeting
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
2
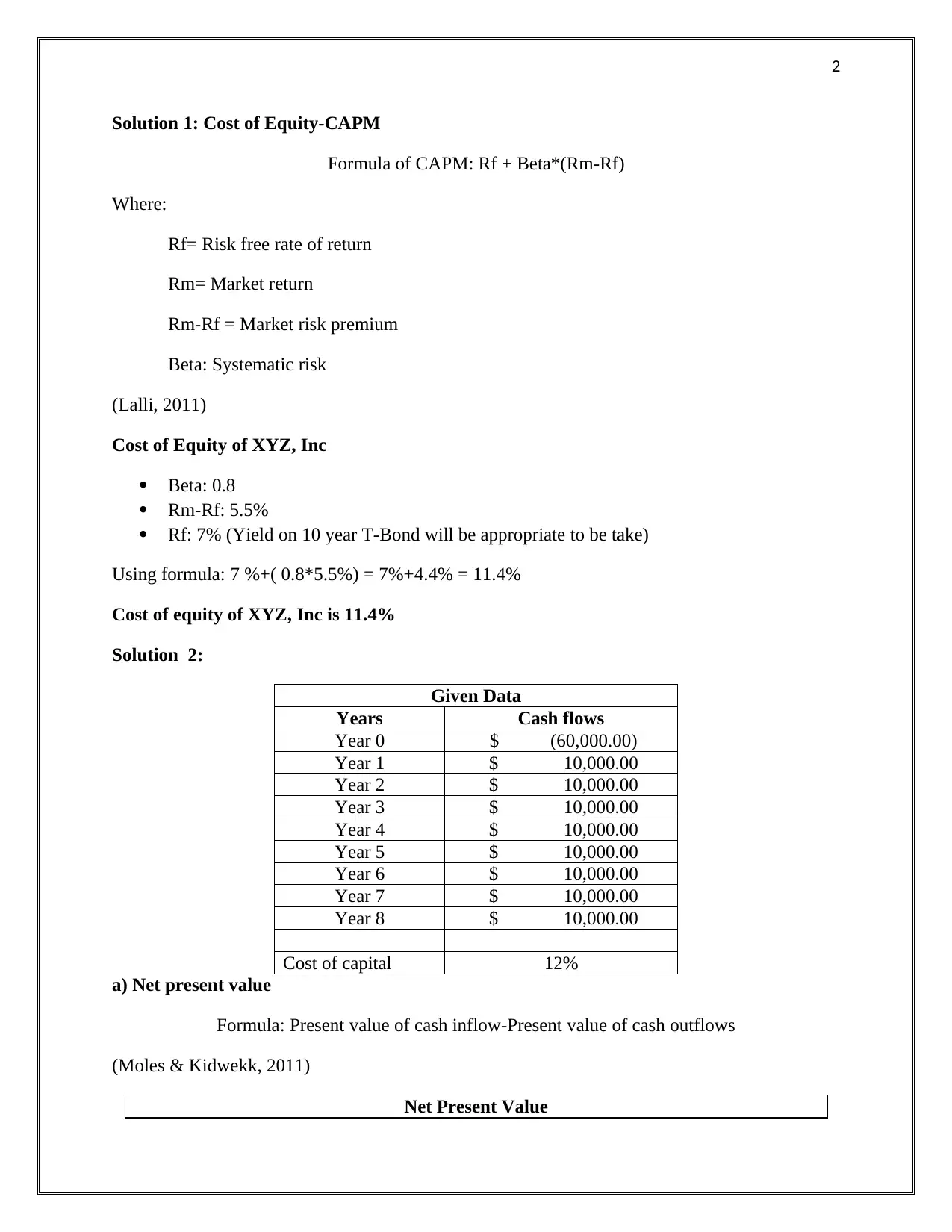
Solution 1: Cost of Equity-CAPM
Formula of CAPM: Rf + Beta*(Rm-Rf)
Where:
Rf= Risk free rate of return
Rm= Market return
Rm-Rf = Market risk premium
Beta: Systematic risk
(Lalli, 2011)
Cost of Equity of XYZ, Inc
Beta: 0.8
Rm-Rf: 5.5%
Rf: 7% (Yield on 10 year T-Bond will be appropriate to be take)
Using formula: 7 %+( 0.8*5.5%) = 7%+4.4% = 11.4%
Cost of equity of XYZ, Inc is 11.4%
Solution 2:
Given Data
Years Cash flows
Year 0 $ (60,000.00)
Year 1 $ 10,000.00
Year 2 $ 10,000.00
Year 3 $ 10,000.00
Year 4 $ 10,000.00
Year 5 $ 10,000.00
Year 6 $ 10,000.00
Year 7 $ 10,000.00
Year 8 $ 10,000.00
Cost of capital 12%
a) Net present value
Formula: Present value of cash inflow-Present value of cash outflows
(Moles & Kidwekk, 2011)
Net Present Value
Solution 1: Cost of Equity-CAPM
Formula of CAPM: Rf + Beta*(Rm-Rf)
Where:
Rf= Risk free rate of return
Rm= Market return
Rm-Rf = Market risk premium
Beta: Systematic risk
(Lalli, 2011)
Cost of Equity of XYZ, Inc
Beta: 0.8
Rm-Rf: 5.5%
Rf: 7% (Yield on 10 year T-Bond will be appropriate to be take)
Using formula: 7 %+( 0.8*5.5%) = 7%+4.4% = 11.4%
Cost of equity of XYZ, Inc is 11.4%
Solution 2:
Given Data
Years Cash flows
Year 0 $ (60,000.00)
Year 1 $ 10,000.00
Year 2 $ 10,000.00
Year 3 $ 10,000.00
Year 4 $ 10,000.00
Year 5 $ 10,000.00
Year 6 $ 10,000.00
Year 7 $ 10,000.00
Year 8 $ 10,000.00
Cost of capital 12%
a) Net present value
Formula: Present value of cash inflow-Present value of cash outflows
(Moles & Kidwekk, 2011)
Net Present Value
3
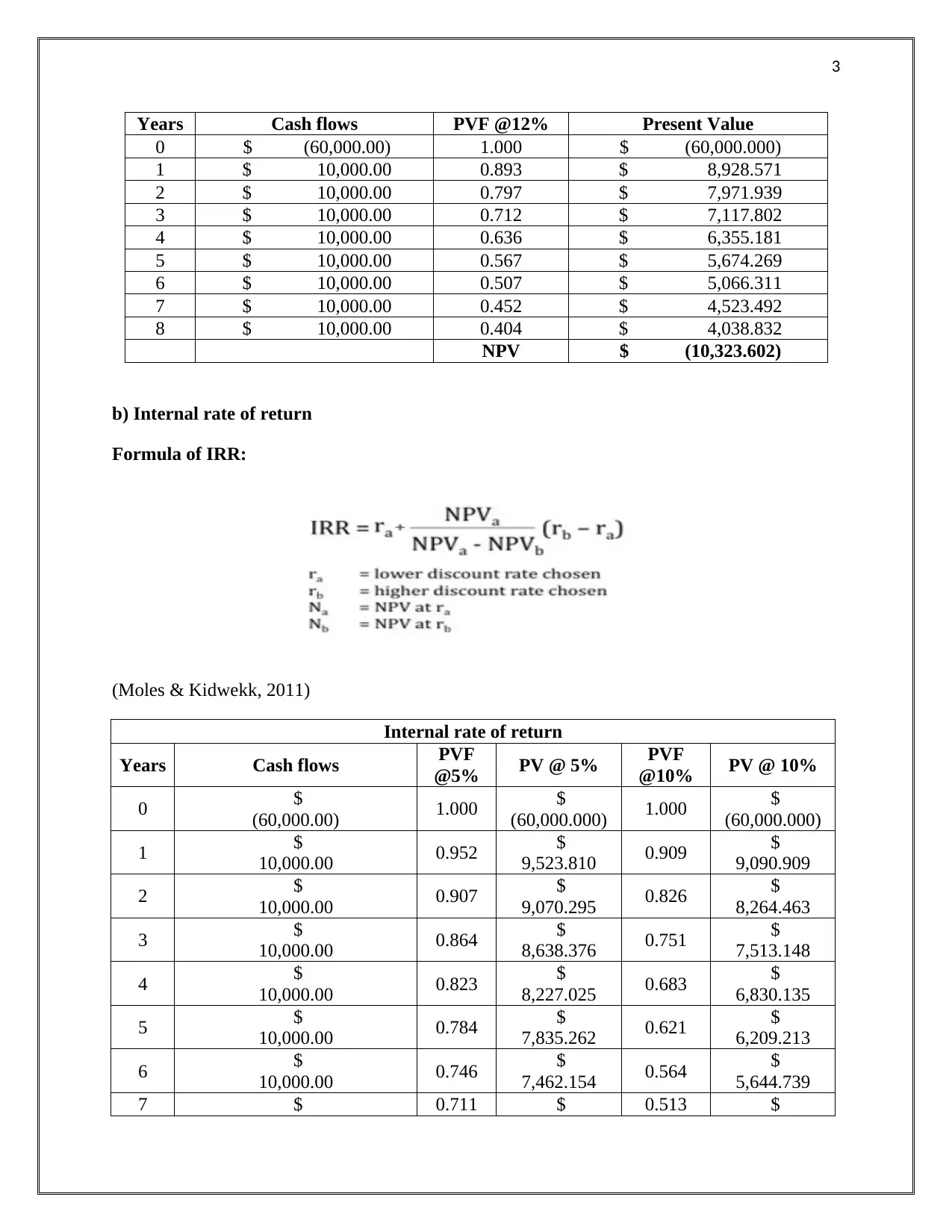
Years Cash flows PVF @12% Present Value
0 $ (60,000.00) 1.000 $ (60,000.000)
1 $ 10,000.00 0.893 $ 8,928.571
2 $ 10,000.00 0.797 $ 7,971.939
3 $ 10,000.00 0.712 $ 7,117.802
4 $ 10,000.00 0.636 $ 6,355.181
5 $ 10,000.00 0.567 $ 5,674.269
6 $ 10,000.00 0.507 $ 5,066.311
7 $ 10,000.00 0.452 $ 4,523.492
8 $ 10,000.00 0.404 $ 4,038.832
NPV $ (10,323.602)
b) Internal rate of return
Formula of IRR:
(Moles & Kidwekk, 2011)
Internal rate of return
Years Cash flows PVF
@5% PV @ 5% PVF
@10% PV @ 10%
0 $
(60,000.00) 1.000 $
(60,000.000) 1.000 $
(60,000.000)
1 $
10,000.00 0.952 $
9,523.810 0.909 $
9,090.909
2 $
10,000.00 0.907 $
9,070.295 0.826 $
8,264.463
3 $
10,000.00 0.864 $
8,638.376 0.751 $
7,513.148
4 $
10,000.00 0.823 $
8,227.025 0.683 $
6,830.135
5 $
10,000.00 0.784 $
7,835.262 0.621 $
6,209.213
6 $
10,000.00 0.746 $
7,462.154 0.564 $
5,644.739
7 $ 0.711 $ 0.513 $
Years Cash flows PVF @12% Present Value
0 $ (60,000.00) 1.000 $ (60,000.000)
1 $ 10,000.00 0.893 $ 8,928.571
2 $ 10,000.00 0.797 $ 7,971.939
3 $ 10,000.00 0.712 $ 7,117.802
4 $ 10,000.00 0.636 $ 6,355.181
5 $ 10,000.00 0.567 $ 5,674.269
6 $ 10,000.00 0.507 $ 5,066.311
7 $ 10,000.00 0.452 $ 4,523.492
8 $ 10,000.00 0.404 $ 4,038.832
NPV $ (10,323.602)
b) Internal rate of return
Formula of IRR:
(Moles & Kidwekk, 2011)
Internal rate of return
Years Cash flows PVF
@5% PV @ 5% PVF
@10% PV @ 10%
0 $
(60,000.00) 1.000 $
(60,000.000) 1.000 $
(60,000.000)
1 $
10,000.00 0.952 $
9,523.810 0.909 $
9,090.909
2 $
10,000.00 0.907 $
9,070.295 0.826 $
8,264.463
3 $
10,000.00 0.864 $
8,638.376 0.751 $
7,513.148
4 $
10,000.00 0.823 $
8,227.025 0.683 $
6,830.135
5 $
10,000.00 0.784 $
7,835.262 0.621 $
6,209.213
6 $
10,000.00 0.746 $
7,462.154 0.564 $
5,644.739
7 $ 0.711 $ 0.513 $
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
4
10,000.00 7,106.813 5,131.581
8 $
10,000.00 0.677 $
6,768.394 0.467 $
4,665.074
NPV $
4,632.128 NPV $
(6,650.738)
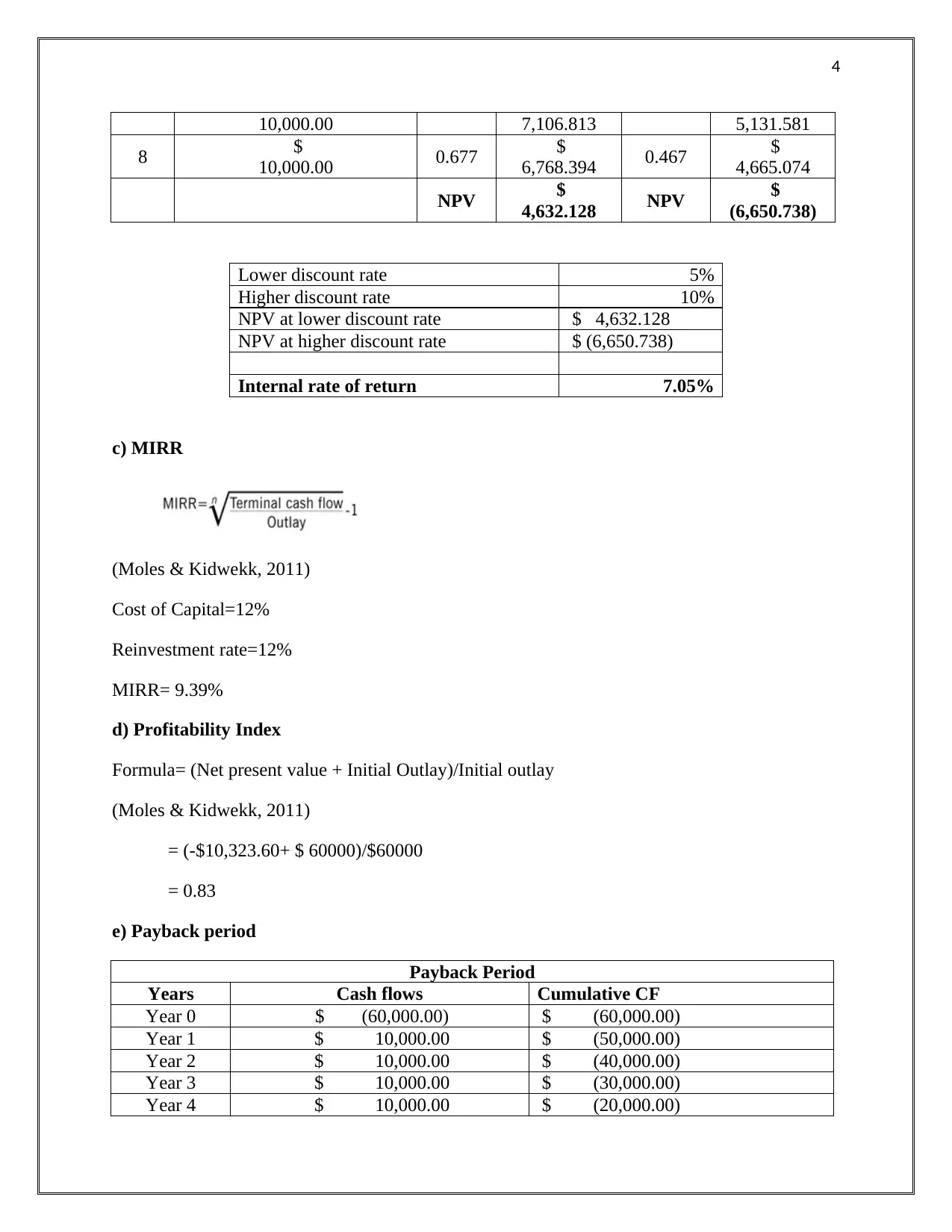
Lower discount rate 5%
Higher discount rate 10%
NPV at lower discount rate $ 4,632.128
NPV at higher discount rate $ (6,650.738)
Internal rate of return 7.05%
c) MIRR
(Moles & Kidwekk, 2011)
Cost of Capital=12%
Reinvestment rate=12%
MIRR= 9.39%
d) Profitability Index
Formula= (Net present value + Initial Outlay)/Initial outlay
(Moles & Kidwekk, 2011)
= (-$10,323.60+ $ 60000)/$60000
= 0.83
e) Payback period
Payback Period
Years Cash flows Cumulative CF
Year 0 $ (60,000.00) $ (60,000.00)
Year 1 $ 10,000.00 $ (50,000.00)
Year 2 $ 10,000.00 $ (40,000.00)
Year 3 $ 10,000.00 $ (30,000.00)
Year 4 $ 10,000.00 $ (20,000.00)
10,000.00 7,106.813 5,131.581
8 $
10,000.00 0.677 $
6,768.394 0.467 $
4,665.074
NPV $
4,632.128 NPV $
(6,650.738)
Lower discount rate 5%
Higher discount rate 10%
NPV at lower discount rate $ 4,632.128
NPV at higher discount rate $ (6,650.738)
Internal rate of return 7.05%
c) MIRR
(Moles & Kidwekk, 2011)
Cost of Capital=12%
Reinvestment rate=12%
MIRR= 9.39%
d) Profitability Index
Formula= (Net present value + Initial Outlay)/Initial outlay
(Moles & Kidwekk, 2011)
= (-$10,323.60+ $ 60000)/$60000
= 0.83
e) Payback period
Payback Period
Years Cash flows Cumulative CF
Year 0 $ (60,000.00) $ (60,000.00)
Year 1 $ 10,000.00 $ (50,000.00)
Year 2 $ 10,000.00 $ (40,000.00)
Year 3 $ 10,000.00 $ (30,000.00)
Year 4 $ 10,000.00 $ (20,000.00)
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
5
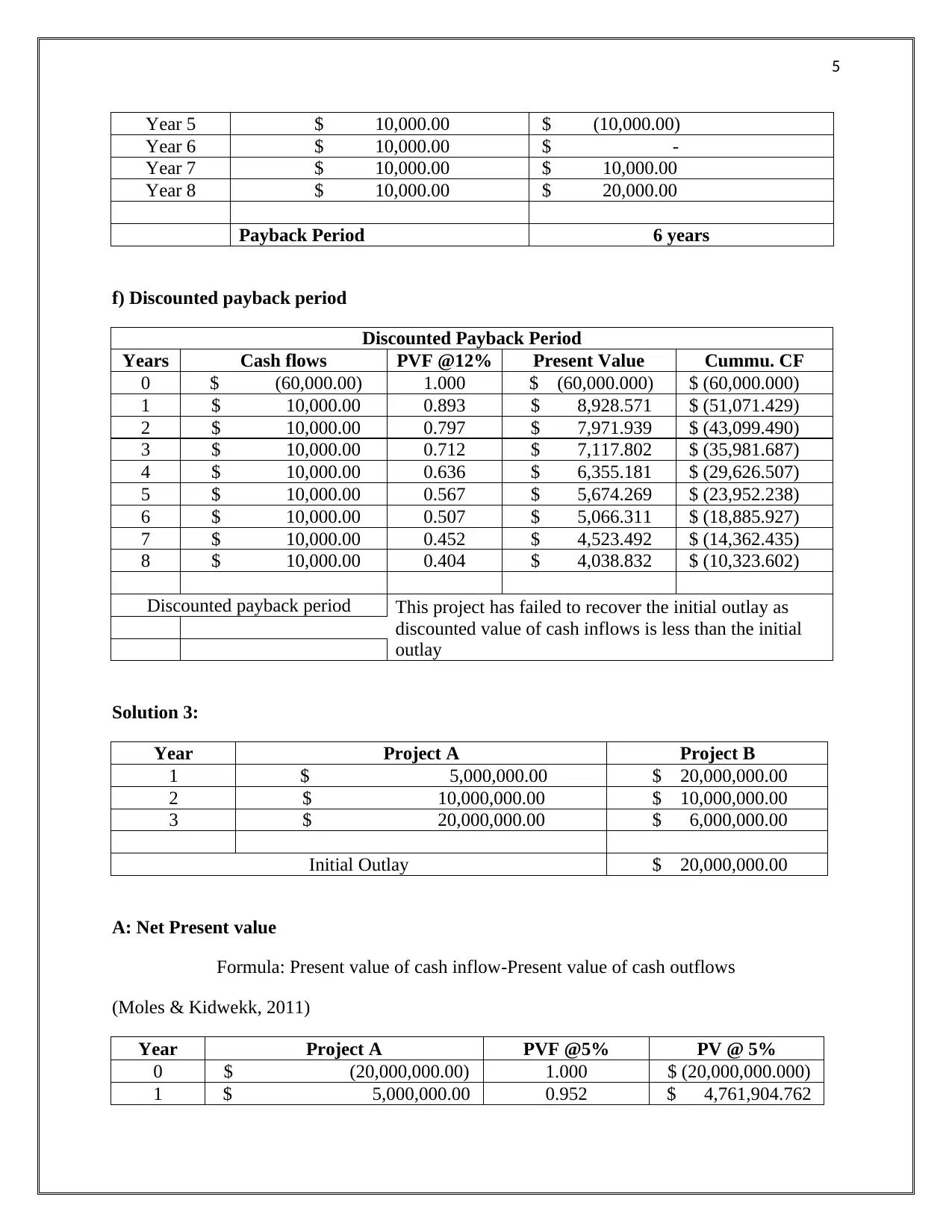
Year 5 $ 10,000.00 $ (10,000.00)
Year 6 $ 10,000.00 $ -
Year 7 $ 10,000.00 $ 10,000.00
Year 8 $ 10,000.00 $ 20,000.00
Payback Period 6 years
f) Discounted payback period
Discounted Payback Period
Years Cash flows PVF @12% Present Value Cummu. CF
0 $ (60,000.00) 1.000 $ (60,000.000) $ (60,000.000)
1 $ 10,000.00 0.893 $ 8,928.571 $ (51,071.429)
2 $ 10,000.00 0.797 $ 7,971.939 $ (43,099.490)
3 $ 10,000.00 0.712 $ 7,117.802 $ (35,981.687)
4 $ 10,000.00 0.636 $ 6,355.181 $ (29,626.507)
5 $ 10,000.00 0.567 $ 5,674.269 $ (23,952.238)
6 $ 10,000.00 0.507 $ 5,066.311 $ (18,885.927)
7 $ 10,000.00 0.452 $ 4,523.492 $ (14,362.435)
8 $ 10,000.00 0.404 $ 4,038.832 $ (10,323.602)
Discounted payback period This project has failed to recover the initial outlay as
discounted value of cash inflows is less than the initial
outlay
Solution 3:
Year Project A Project B
1 $ 5,000,000.00 $ 20,000,000.00
2 $ 10,000,000.00 $ 10,000,000.00
3 $ 20,000,000.00 $ 6,000,000.00
Initial Outlay $ 20,000,000.00
A: Net Present value
Formula: Present value of cash inflow-Present value of cash outflows
(Moles & Kidwekk, 2011)
Year Project A PVF @5% PV @ 5%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 5,000,000.00 0.952 $ 4,761,904.762
Year 5 $ 10,000.00 $ (10,000.00)
Year 6 $ 10,000.00 $ -
Year 7 $ 10,000.00 $ 10,000.00
Year 8 $ 10,000.00 $ 20,000.00
Payback Period 6 years
f) Discounted payback period
Discounted Payback Period
Years Cash flows PVF @12% Present Value Cummu. CF
0 $ (60,000.00) 1.000 $ (60,000.000) $ (60,000.000)
1 $ 10,000.00 0.893 $ 8,928.571 $ (51,071.429)
2 $ 10,000.00 0.797 $ 7,971.939 $ (43,099.490)
3 $ 10,000.00 0.712 $ 7,117.802 $ (35,981.687)
4 $ 10,000.00 0.636 $ 6,355.181 $ (29,626.507)
5 $ 10,000.00 0.567 $ 5,674.269 $ (23,952.238)
6 $ 10,000.00 0.507 $ 5,066.311 $ (18,885.927)
7 $ 10,000.00 0.452 $ 4,523.492 $ (14,362.435)
8 $ 10,000.00 0.404 $ 4,038.832 $ (10,323.602)
Discounted payback period This project has failed to recover the initial outlay as
discounted value of cash inflows is less than the initial
outlay
Solution 3:
Year Project A Project B
1 $ 5,000,000.00 $ 20,000,000.00
2 $ 10,000,000.00 $ 10,000,000.00
3 $ 20,000,000.00 $ 6,000,000.00
Initial Outlay $ 20,000,000.00
A: Net Present value
Formula: Present value of cash inflow-Present value of cash outflows
(Moles & Kidwekk, 2011)
Year Project A PVF @5% PV @ 5%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 5,000,000.00 0.952 $ 4,761,904.762
6
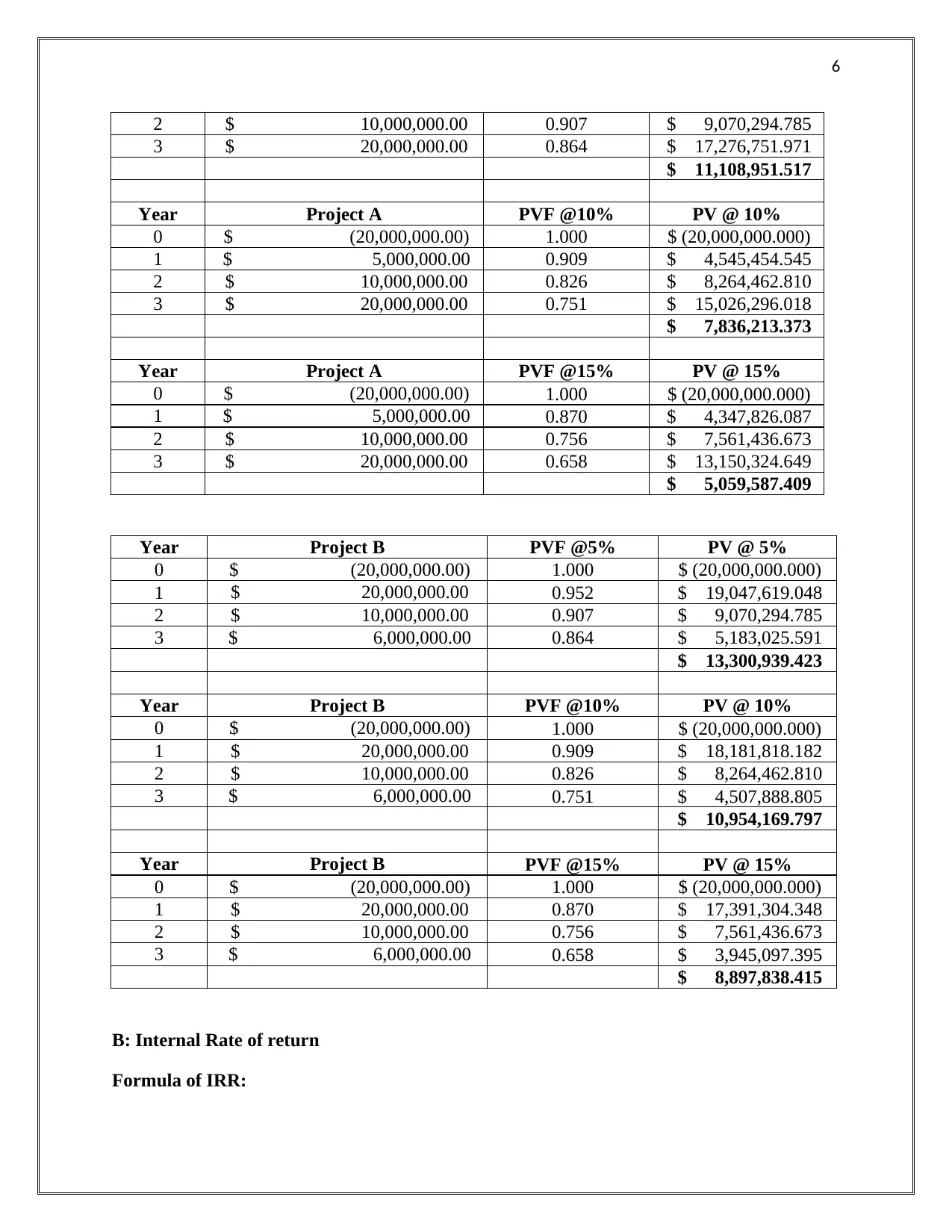
2 $ 10,000,000.00 0.907 $ 9,070,294.785
3 $ 20,000,000.00 0.864 $ 17,276,751.971
$ 11,108,951.517
Year Project A PVF @10% PV @ 10%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 5,000,000.00 0.909 $ 4,545,454.545
2 $ 10,000,000.00 0.826 $ 8,264,462.810
3 $ 20,000,000.00 0.751 $ 15,026,296.018
$ 7,836,213.373
Year Project A PVF @15% PV @ 15%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 5,000,000.00 0.870 $ 4,347,826.087
2 $ 10,000,000.00 0.756 $ 7,561,436.673
3 $ 20,000,000.00 0.658 $ 13,150,324.649
$ 5,059,587.409
Year Project B PVF @5% PV @ 5%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 20,000,000.00 0.952 $ 19,047,619.048
2 $ 10,000,000.00 0.907 $ 9,070,294.785
3 $ 6,000,000.00 0.864 $ 5,183,025.591
$ 13,300,939.423
Year Project B PVF @10% PV @ 10%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 20,000,000.00 0.909 $ 18,181,818.182
2 $ 10,000,000.00 0.826 $ 8,264,462.810
3 $ 6,000,000.00 0.751 $ 4,507,888.805
$ 10,954,169.797
Year Project B PVF @15% PV @ 15%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 20,000,000.00 0.870 $ 17,391,304.348
2 $ 10,000,000.00 0.756 $ 7,561,436.673
3 $ 6,000,000.00 0.658 $ 3,945,097.395
$ 8,897,838.415
B: Internal Rate of return
Formula of IRR:
2 $ 10,000,000.00 0.907 $ 9,070,294.785
3 $ 20,000,000.00 0.864 $ 17,276,751.971
$ 11,108,951.517
Year Project A PVF @10% PV @ 10%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 5,000,000.00 0.909 $ 4,545,454.545
2 $ 10,000,000.00 0.826 $ 8,264,462.810
3 $ 20,000,000.00 0.751 $ 15,026,296.018
$ 7,836,213.373
Year Project A PVF @15% PV @ 15%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 5,000,000.00 0.870 $ 4,347,826.087
2 $ 10,000,000.00 0.756 $ 7,561,436.673
3 $ 20,000,000.00 0.658 $ 13,150,324.649
$ 5,059,587.409
Year Project B PVF @5% PV @ 5%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 20,000,000.00 0.952 $ 19,047,619.048
2 $ 10,000,000.00 0.907 $ 9,070,294.785
3 $ 6,000,000.00 0.864 $ 5,183,025.591
$ 13,300,939.423
Year Project B PVF @10% PV @ 10%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 20,000,000.00 0.909 $ 18,181,818.182
2 $ 10,000,000.00 0.826 $ 8,264,462.810
3 $ 6,000,000.00 0.751 $ 4,507,888.805
$ 10,954,169.797
Year Project B PVF @15% PV @ 15%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 20,000,000.00 0.870 $ 17,391,304.348
2 $ 10,000,000.00 0.756 $ 7,561,436.673
3 $ 6,000,000.00 0.658 $ 3,945,097.395
$ 8,897,838.415
B: Internal Rate of return
Formula of IRR:
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
7
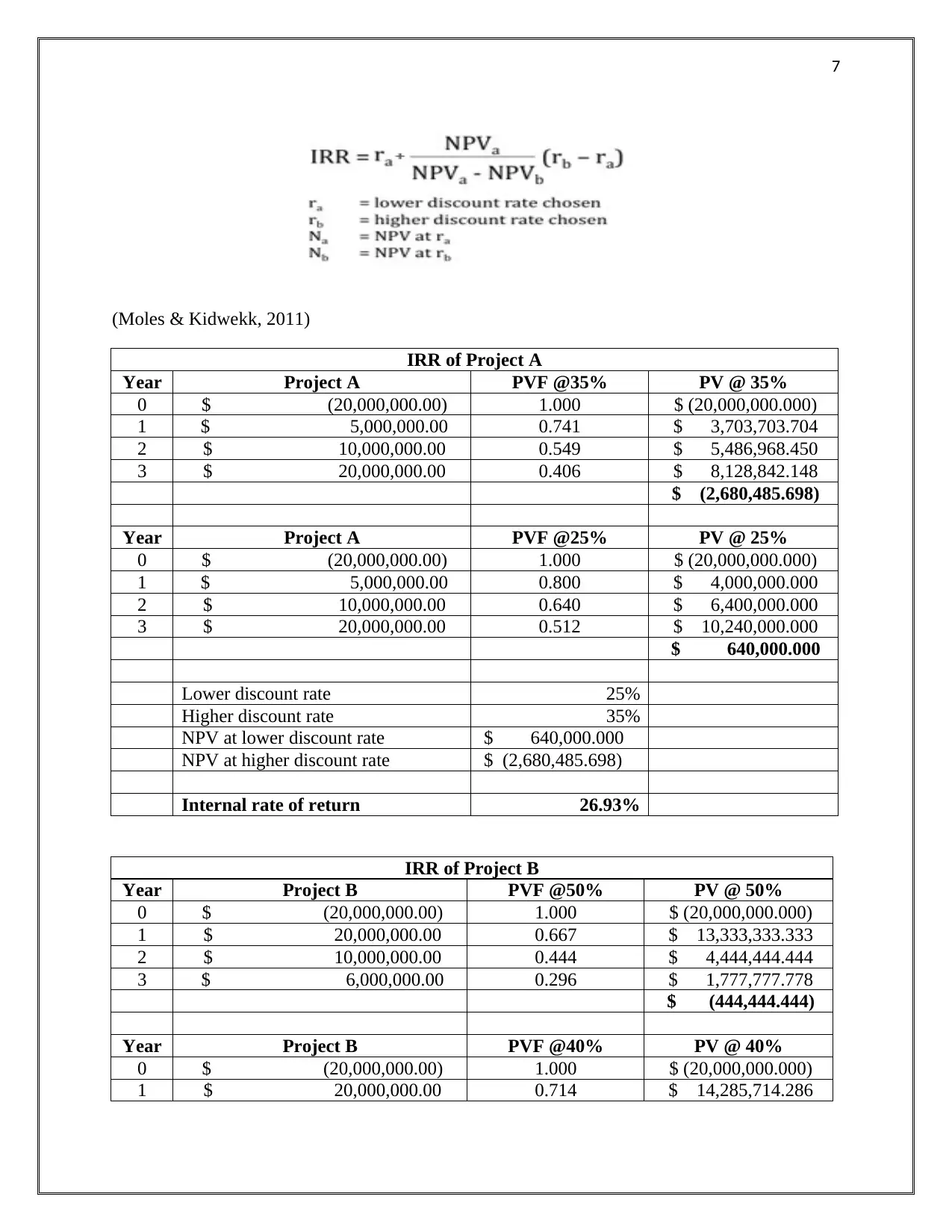
(Moles & Kidwekk, 2011)
IRR of Project A
Year Project A PVF @35% PV @ 35%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 5,000,000.00 0.741 $ 3,703,703.704
2 $ 10,000,000.00 0.549 $ 5,486,968.450
3 $ 20,000,000.00 0.406 $ 8,128,842.148
$ (2,680,485.698)
Year Project A PVF @25% PV @ 25%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 5,000,000.00 0.800 $ 4,000,000.000
2 $ 10,000,000.00 0.640 $ 6,400,000.000
3 $ 20,000,000.00 0.512 $ 10,240,000.000
$ 640,000.000
Lower discount rate 25%
Higher discount rate 35%
NPV at lower discount rate $ 640,000.000
NPV at higher discount rate $ (2,680,485.698)
Internal rate of return 26.93%
IRR of Project B
Year Project B PVF @50% PV @ 50%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 20,000,000.00 0.667 $ 13,333,333.333
2 $ 10,000,000.00 0.444 $ 4,444,444.444
3 $ 6,000,000.00 0.296 $ 1,777,777.778
$ (444,444.444)
Year Project B PVF @40% PV @ 40%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 20,000,000.00 0.714 $ 14,285,714.286
(Moles & Kidwekk, 2011)
IRR of Project A
Year Project A PVF @35% PV @ 35%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 5,000,000.00 0.741 $ 3,703,703.704
2 $ 10,000,000.00 0.549 $ 5,486,968.450
3 $ 20,000,000.00 0.406 $ 8,128,842.148
$ (2,680,485.698)
Year Project A PVF @25% PV @ 25%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 5,000,000.00 0.800 $ 4,000,000.000
2 $ 10,000,000.00 0.640 $ 6,400,000.000
3 $ 20,000,000.00 0.512 $ 10,240,000.000
$ 640,000.000
Lower discount rate 25%
Higher discount rate 35%
NPV at lower discount rate $ 640,000.000
NPV at higher discount rate $ (2,680,485.698)
Internal rate of return 26.93%
IRR of Project B
Year Project B PVF @50% PV @ 50%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 20,000,000.00 0.667 $ 13,333,333.333
2 $ 10,000,000.00 0.444 $ 4,444,444.444
3 $ 6,000,000.00 0.296 $ 1,777,777.778
$ (444,444.444)
Year Project B PVF @40% PV @ 40%
0 $ (20,000,000.00) 1.000 $ (20,000,000.000)
1 $ 20,000,000.00 0.714 $ 14,285,714.286
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
8
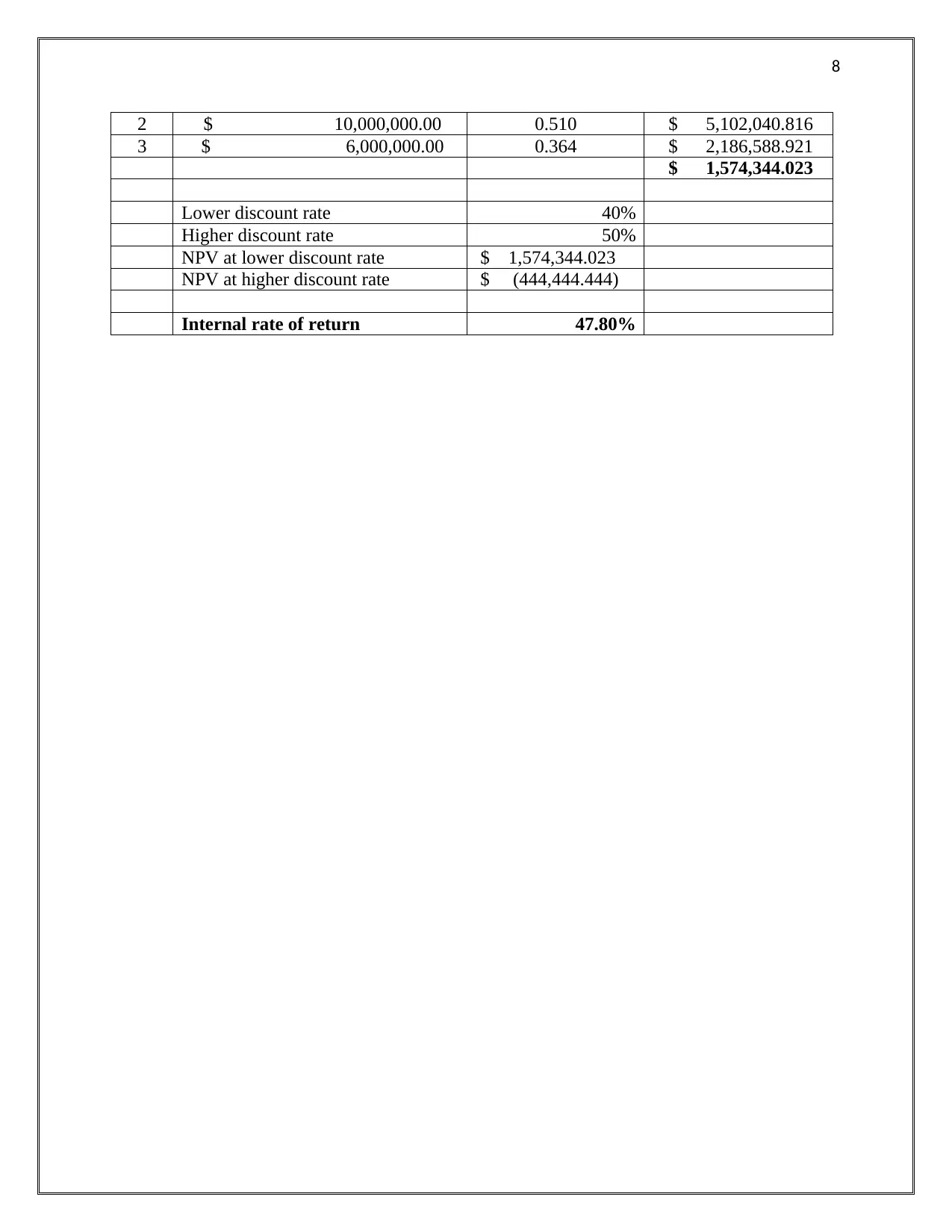
2 $ 10,000,000.00 0.510 $ 5,102,040.816
3 $ 6,000,000.00 0.364 $ 2,186,588.921
$ 1,574,344.023
Lower discount rate 40%
Higher discount rate 50%
NPV at lower discount rate $ 1,574,344.023
NPV at higher discount rate $ (444,444.444)
Internal rate of return 47.80%
2 $ 10,000,000.00 0.510 $ 5,102,040.816
3 $ 6,000,000.00 0.364 $ 2,186,588.921
$ 1,574,344.023
Lower discount rate 40%
Higher discount rate 50%
NPV at lower discount rate $ 1,574,344.023
NPV at higher discount rate $ (444,444.444)
Internal rate of return 47.80%

9
References
Lalli, W. (2011). Handbook of Budgeting. US: John Wiley & Sons.
Moles, P. & Kidwekk, D. (2011). Corporate finance. US: John Wiley &sons.
References
Lalli, W. (2011). Handbook of Budgeting. US: John Wiley & Sons.
Moles, P. & Kidwekk, D. (2011). Corporate finance. US: John Wiley &sons.
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





