Enterprise Risk Modelling: Outpatient Waiting Times at GCU London

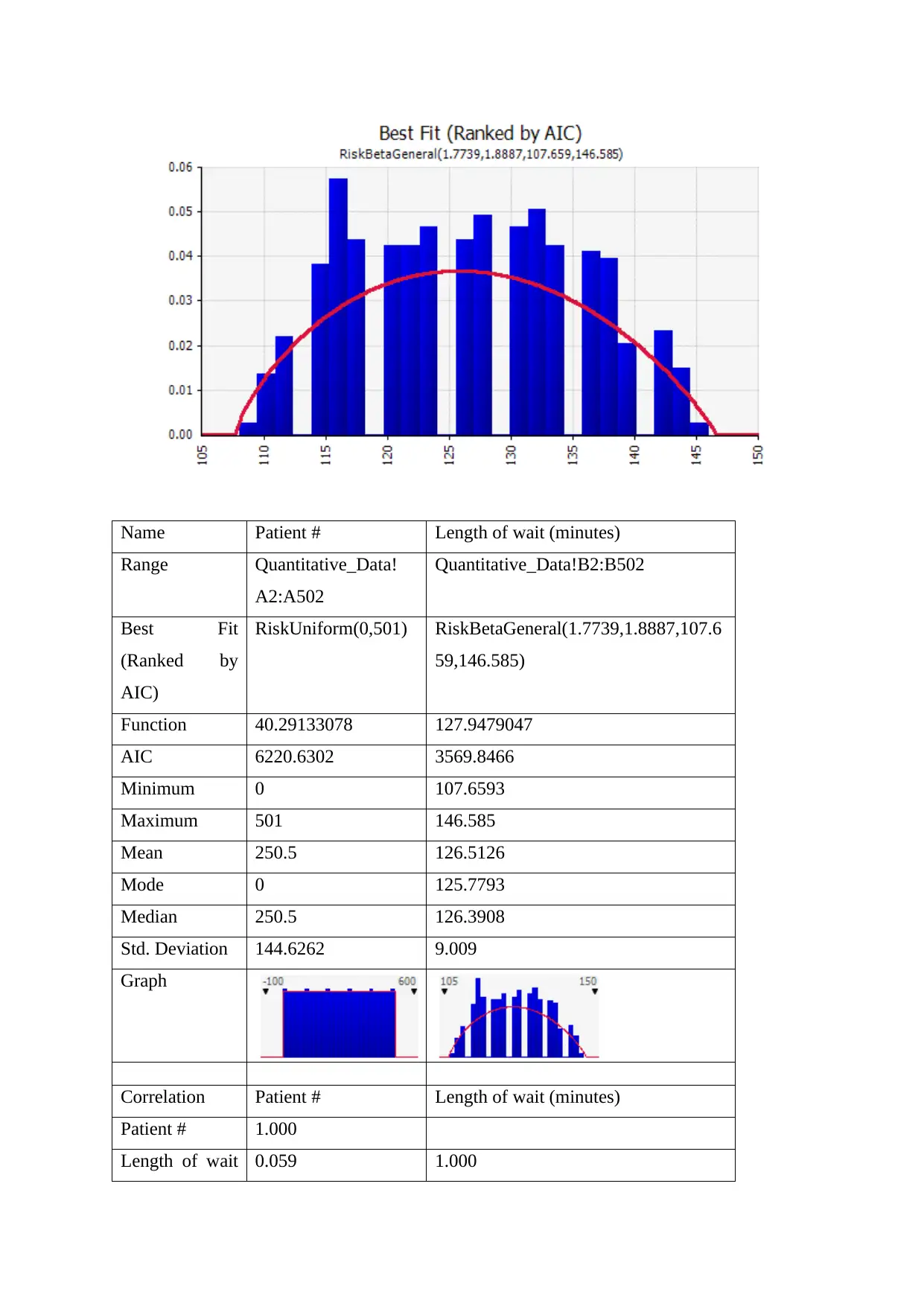
This project analyses outpatient waiting times at a local hospital, focusing on the risk of exceeding the government-mandated 120-minute waiting time limit and accruing penalty points. The analysis uses quantitative data to determine the expected minimum, maximum, and mean number of penalty points. The Distribution Fitting Facility is employed to identify an appropriate probability distribution governing wait times, with RiskUniform and RiskBetaGeneral distributions being considered. A 1000-iteration simulation estimates the probability distribution of additional penalty points, utilizing functions like RiskUniform and RiskBetaGeneral. The project uses @Risk Excel add-on in conjunction with Excel to derive a working solution to the problem.

Enterprise Risk Modelling

Table of Contents
Project Description..............................................................................................................................1
Question 1............................................................................................................................................1
Question 2............................................................................................................................................2
Question 3............................................................................................................................................4
References............................................................................................................................................6

Project Description
This project is analysis the outpatient waiting times for provided quantitative data.
The provided data is based on the patients because basically patients are come to the local
hospital accidents and emergency department or treatment. But, the patients are wait until a
doctor or nurse is available to the treat them. Basically, the government has set the maximum
length of waiting time for each patient must been have treated. The maximum waiting time is
12o minutes. So, if patients are wait longer than this maximum, it will result in the hospital
being awarded penalty points at the rate of 10 points per minute over the maximum. So, this
project is needs to determine the total number of penalty points the hospital accrues over the
year by using the Risk solver on Excel. These are will be discussed and analysed in detail.
Question 1
First, we are determine the expected minimu, maximum and mean number of the
penalty points. It is represented as below.

Question 2
Here, we are using the Distribution Fitting Facility to determine an appropriate probability
distribution that appears to govern the wait time. It is represented as below (solver, 2018).

Name Patient # Length of wait (minutes)
Range Quantitative_Data!
A2:A502
Quantitative_Data!B2:B502
Best Fit
(Ranked by
AIC)
RiskUniform(0,501) RiskBetaGeneral(1.7739,1.8887,107.6
59,146.585)
Function 40.29133078 127.9479047
AIC 6220.6302 3569.8466
Minimum 0 107.6593
Maximum 501 146.585
Mean 250.5 126.5126
Mode 0 125.7793
Median 250.5 126.3908
Std. Deviation 144.6262 9.009
Graph
Correlation Patient # Length of wait (minutes)
Patient # 1.000
Length of wait 0.059 1.000

(minutes)
Question 3
Here, we hare perform the 1000 iteration simulation of the waiting times to estimate
the probability distribution of the additional penalty points. It is represented as below
(Albright et al., 2011).

Name
Ce
ll
Function
Min Mea
n
Max
Correlation Matrix: Location: 'Fit Summary '!$B$20:$C$21
Size: 2 X 2
Function /
RiskUniform(0,501)
B
9
RiskUniform(0,501,RiskCorrmat($B$20:$C$2
1,1))
0 250.
5
501
Function /
RiskBetaGeneral(1.7739,1.8
887,107.659,146.585)
C
9
RiskBetaGeneral(1.7739,1.8887,107.659,146.
585,RiskCorrmat($B$20:$C$21,2))
107.
659
126.
512
146.
585
5.0% 90.0% 5.0%
4.9% 90.0% 5.1%
112.03 141.31
105 110 115 120 125 130 13
0.000
0.005
0.010
0.015
0.020
0.025
0.030
0.035
0.040
Function / RiskBetaGeneral(1.7739,1.8887,107.659,146.585)
Comparison with BetaGeneral(1.7739,1.8887,107.659,146.585)
References
Albright, S., Winston, W., Zappe, C. and Broadie, M. (2011). Data analysis, optimization,
and simulation modeling. Australia: Cengage Learning.
solver. (2018). Risk Solver® Platform. [online] Available at: https://www.solver.com/risk-
solver%C2%AE-platform [Accessed 29 Dec. 2018].