Geometry - Unit Test, Part 2: Solutions and Explanations

This document contains detailed solutions for a geometry unit test, covering a wide range of topics including similar shapes, three-dimensional figures and graphs, surface area and volume, circles, trigonometry, and beyond Euclidean geometry. The solutions include step-by-step explanations, diagrams, and formulas to help students understand the concepts and solve the problems. The test also includes a semester review with solutions. The solutions are presented in a clear and organized manner, making it easy for students to follow along and learn from their mistakes. The document aims to provide a comprehensive guide for students preparing for their geometry unit tests and semester exams. The document covers topics like reflection, translation, scale factors, and calculations for surface area, volume, and angles within different geometric shapes. The solutions also include explanations of Euler's path and circuit theory, as well as conversions between binary and decimal number systems.

Question and Answer
1 | P a g e
Geometry

Question and Answer
Contents
Unit Test, Part 2: Similar Shapes.....................................................................................................4
Solution of 1a...............................................................................................................................4
Solution of 1b..............................................................................................................................4
Solution of 2a...............................................................................................................................4
Solution of 2b..............................................................................................................................5
Solution of 2c...............................................................................................................................5
Solution of 2d..............................................................................................................................6
Unit Test, Part 2: Three-Dimensional Figures and Graphs.............................................................6
Solution 1a...................................................................................................................................6
Solution 1b...................................................................................................................................6
Solution 1.....................................................................................................................................6
Solution 2.....................................................................................................................................6
Solution 3.....................................................................................................................................7
Unit Test, Part 2: Surface Area and Volume...................................................................................8
Solution 1a...................................................................................................................................8
Solution 1b...................................................................................................................................8
Solution 1c...................................................................................................................................8
Solution 1d...................................................................................................................................9
Solution 2a...................................................................................................................................9
Solution 2b...................................................................................................................................9
Solution 2c...................................................................................................................................9
Solution 2d.................................................................................................................................10
Unit Test, Part 2: Circles...............................................................................................................10
Solution 1...................................................................................................................................10
Solution 2a.................................................................................................................................11
Solution 2b.................................................................................................................................11
Solution 2c.................................................................................................................................11
Unit Test, Part 2: Trigonometry.....................................................................................................12
Solution 1a.................................................................................................................................12
Solution 1b.................................................................................................................................12
2 | P a g e

Question and Answer
Unit Test, Part 2: Beyond Euclidean Geometry............................................................................12
Solution 1a.................................................................................................................................12
Solution 1b.................................................................................................................................12
Solution 1c.................................................................................................................................13
Solution 2a.................................................................................................................................13
Solution 2b.................................................................................................................................13
Solution 2c.................................................................................................................................13
Solution 2d.................................................................................................................................13
Solution 3a.................................................................................................................................13
Solution 3b.................................................................................................................................13
Semester Test, Part 2: Semester Review and Test.........................................................................14
Solution 1...................................................................................................................................14
Solution 2...................................................................................................................................15
Solution 3a.................................................................................................................................15
Solution 3b.................................................................................................................................15
Solution 4a.................................................................................................................................16
Solution 4b.................................................................................................................................16
Solution 4c.................................................................................................................................16
Solution 4d.................................................................................................................................16
3 | P a g e

Question and Answer
Unit Test, Part 2: Similar Shapes
Solution of 1a
As given in question, the two-column proof are given below
Statement Reason
<ATN = <ATN Both are common
Side AT ~ side RT AN // to NI,
Side TN ~ side TJ AN // to NI,
From side angle side theorem, △ tan △ TRI Proved
Solution of 1b
As per side splitting theorem, we will proportionate the side as per similarity triangle.
△ tan △ TRI
The sides, AT
RA = TN
¿ Putting the value given,
8
2 = 12
¿ or, ¿=12∗2
8 =3 cm Ans
Solution of 2a
Since, both are pyramid is square, both are symmetrical
hl =12m , hs=6 m
vl =400 m3 V s =?
The height of larger pyramid is given as = hL=12m ,
The height of larger pyramid is given as = hS=6 m ,
,
4 | P a g e

Question and Answer
Scale factor for both pyramid = hS
hL
= 6
12 =1 :2 Ans
Solution of 2b
We will use the solution calculated in 2a
Since scale factor smaller to larger pyramid = 1:2
Area is square of side
Ration of both pyramids was given as
Or, aS
2
aL
2 =( 1
2 ) 2
, aS
2
aL
2 = 1
4
Since area is square of sides
From the calculation, area of bases is are in the ration = ¼
Solution of 2c
Since we have calculated, hS
hL
=1
2, aS
2
aL
2 = 1
4
The volume is given by V s =1
3 x hs x as
2
for smaller pyramid
The volume is given by V L= 1
3 x hL x aL
2 for larger pyramid
Ratio of both pyramid = V s
V L
= hs x as
2
hL x aL
2 =1
2 x 1
4 =1
8
The ration of volume = V s
V L
=1:8
Solution of 2d
From above calculation we know that, V s
V L
=1:8 and VL = 400 m3
5 | P a g e

Question and Answer
Then V s = 400
8 =50 m3
The volume of smaller pyramid = 50 m3 Ans
Unit Test, Part 2: Three-Dimensional Figures and Graphs
Solution 1a
As we all know that, the right rectangular prism, consists of six surfaces, and twelve edges. For
surface area measurement, we will measure all edges of the prism, the surface area will be four
time of multiplication of length and width, and two time of square of the sides. For the case of
volume calculation, we will look for square of the side, multiplied by length of the prism.
Solution 1b
The unit of surface area is same as unit of area and it m2 in SI or MKS unit, while unit of volume
is m3, in SI or MKS unit. The reason of unit of surface area is m2 is due to during area
calculation, we multiply two different length unit and its product becomes square of single unit
i.e. m2. For the case of volume, there are three different length unit s are used, i.e. length, breadth
and height. The product of these three unit becomes cube of the unit i.e. m3.
Solution 1
The measurement of surface area is required when, there is requirement of cost on
painting, wallpaper fixing or cleaning. The cost of these work generally related with cost per unit
square of the area, which is multiplied with the area calculated to find the total cost of painting.
The volume is required to find out the quantity of material, i.e. to find the number of bricks used
in making the structure. In this condition we required to find the volume of solid structure and
volume of one brick. The volume of structure is divided by volume of bricks, and the result is
number of ricks. There are several other examples where volume is being used, most of the
liquid are being used in cc or m3, which is the unit of volume, because liquid takes place the
shapes of container, which volume can be measured.
Solution 2
As given in question,
Suppose the point are P, Q, and R are the coordinate of the point is given as
P = (3,0,0)
6 | P a g e

Question and Answer
Q = (0,8,0)
R = (0,0,6)
The plane PQ can be represented as PQ = (0-3), (8-0), (0-0) = (-3, 8, 0)
The plane QR can be represented as PR = (0-3), (0-0), (6-0) = (-3, 0, 6)
The normal vector for given plane will be ⃗ PQ x⃗ PR⃗
PQ x⃗ PR = | A B C
−3 8 0
−3 0 6 |
Solving the determinant, we get ⃗
PQ x⃗ PR=¿48A+18B+24C
Suppose, PX is the plane which is perpendicular to ⃗ PQ x⃗ PR=¿⃗
PQ x⃗ PR x⃗ PX=¿ 0,
Putting the value, (x-3, y, z) (48,18,24) = 48x-144+18y+24z
=48x+18y+24z = 144 dividing by 6
= 8x+3y+4z = 24 Ans
Solution 3
The isometric drawing of rectangular prism is as follows
7 | P a g e

Question and Answer
Unit Test, Part 2: Surface Area and Volume
Solution 1a
The general rule for reflection is that, it changes the sign in third complementary plane,
As given in question, the reflection is in xz plane, the sign will change for the coordinates y
Solution 1b
Then coordinate of the point in reflected plane will be
P’ (0, -5,4), Y’ (-2, -7,4), R (0, -7,4) and A’ (0, -7,6)
Solution 1c
Generally, rules used for translation for reflected image contains the following
terminology with their meaning,
If the translation of image is forward or backward, then there should be change in x coordinates.
If the translation of image is right or left, then there should be change in y coordinates.
If the translation of image is up or down, then there should be change in z coordinates.
Solution 1d
The coordinated of reflected image is as
P’ (0, -5,4), Y’ (-2, -7,4), R (0, -7,4) and A’ (0, -7,6)
As per question, the translated image is three unit back, two unit left and 4 unit up, the
change in coordinate is as follows
P’ (0, -5,4) = P” (0-3, -5-2, 4+4) = P” (-3, -7, 8)
Y’ (-2, -7,4) = Y” (-2-3, -7-2, 4+4) = Y” (-5, -9, 8)
R’ (0, -7,4) = R” (-0-3, -7-2, 4+4) = R” (-3, -9, 8)
8 | P a g e

Question and Answer
A’ (0, -7,6) = R” (-0-3, -7-2, 6+4) = A” (-3, -9, 10)
In this condition, the coordinates of translated image will be P” (-3, -7, 8), Y” (-5, -9, 8), R” (-3, -
9, 8), A” (-3, -9, 10)
Solution 2a
Suppose, the original length, width and height of prism is l, b, and h, and perimeter is p
We know that, if the length, width and height are in x times in scale factor, then its surface area
will be in the multiplication of x2 scale factor.
Then new surface area of prism = actual surface area x scale factor.
New surface area = 360x (1/2)2 = 360/4 = 90 m2 Ans
Solution 2b
Similarly, for volume, if the length width and height are in the scale factor of x then, its
volume will be scale factor of x3
Then new volume of prism = actual volume x scale factor.
V = 60 x (1/2)3 = 60/8 = 7.5 m3
Solution 2c
If length width and height is tripled, then its surface area scale factor will be 32 = 9 times
Then new surface area of prism = actual surface area x scale factor.
New surface area = 360x (3)2 = 360*9 = 3240 m2 Ans
Solution 2d
If length width and height is tripled, then its surface area scale factor will be 33 = 27 times
Then new volume of prism = actual volume x scale factor.
V = 60 x (3)3 = 60*27 = 1620 m3 Ans
9 | P a g e

Question and Answer
Unit Test, Part 2: Circles
Solution 1
As given in question,
m<AED = 48o, m<DAE = 44o
The from triangle ADE, the <ADE = 180 – (44*48) = 88o
For AC perpendicular to EF, the <ADE should be 90o but <ADE = 88o,
Therefore, AD is nor perpendicular to EF Ans
Solution 2a
As given in question,
(x-2)2 + (y+3)2 = 9
From distance formula we know that,
( x−h ) 2+ ( y −k ) 2=r2
The coordinated of the centre of the circle changed sign of numeral in equation,
The coordinates of centre of circle = (2, -3)
10 | P a g e

Question and Answer
Solution 2b
The radius of the circle
R = square root of 9 = 3 unit
And diameter of circle = 3*2 = 6 unit
Solution 2c
The graph and position of circle is as follows
Unit Test, Part 2: Trigonometry
Solution 1a
11 | P a g e

Question and Answer
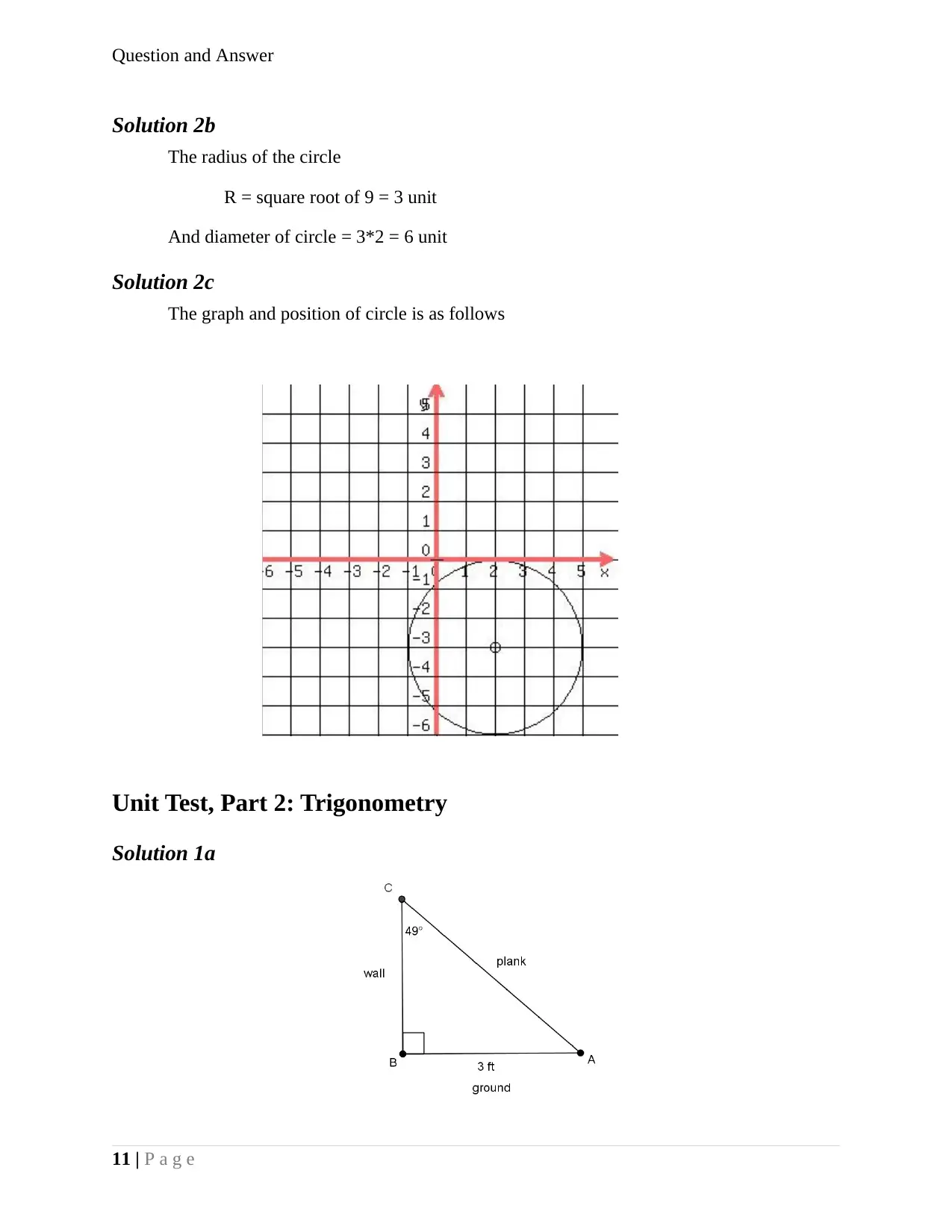
The < CAB = 180o-(49o+90o) = 41o
Using Cos of trigonometry,
Cos 41o = AB/AC, or AC = 3/ Cos 41o = 3/0.745709 = 3.975039 ft Ans
Solution 1b
Using sin ratio of trigonometry
Sin41o = BC/AC, BC = 3.975039 x Sin41o = 2.6079 ft Ans
Unit Test, Part 2: Beyond Euclidean Geometry
Solution 1a
From Euler’s path theory we know that, we can cross every edge, if two odd point are
present and rest other should be other even degree. In the given case, the vertices P and T are odd
degree and rest other are even degree, it means, it satisfies all the criteria of Euler’s path, and in
this condition every edge can be crossed once, the designated path will be P>R>C>M>T>C.P>T.
Solution 1b
As per given graph, all the vertices are not even, in this condition Euler’s circuit, which states
that, we must start and finish at the same point and rest other point must be crossed once. The
given graph does not satisfy the Euler’s circuit criteria and given condition is not possible.
Solution 1c
As we can see in graph, it is quite complex, and in this condition, the trucker must use
Hamiltonian circuit theory. Through this theory one possible route can be obtained, and this
route is J<R<A<V<C<M<T<P<J
Solution 2a
The one important thing in spherical geometry is that, it contradicts the parallel theory of
geometry. The reason is that spherical geometry is not dealing with line but point and circle is
always be there. One more important thing is in spherical geometry, the two great circles always
intersects each other.
12 | P a g e