Geotechnical Engineering Assignment Solution - CE531, [Year]

This geotechnical engineering assignment solution addresses several key concepts in soil mechanics and foundation design. The solution begins by analyzing flow nets and calculating the rate of water removal to prevent flooding, as well as pore water pressure. It proceeds to construct Mohr's circles of effective stress and determine the critical state parameter M. The assignment further involves calculations of vertical stress increase and total settlement using Fadum's chart, followed by a discussion on the limitations of elastic analysis. The solution also defines overconsolidation ratio and related soil classifications, along with calculations of total and effective stresses, pore water pressure, and primary consolidation settlement. Finally, the assignment addresses retaining wall design using Rankine's earth pressure theory, including sketches of stress distributions and calculations of resultant thrust. The document provides a detailed step-by-step solution to all questions.

Running head: GEOTECHNICAL ENGINEERING ASSIGNMENT 1
Geotechnical Engineering Assignment
Firstname Lastname
Name of Institution

GEOTECHNICAL ENGINEERING ASSIGNMENT 2
Question 1
a) Draw the flow net assuming the soil is isotropic and the water level inside the sheet
piles is maintained at excavation level.
8 m
4 m
b) Estimate the rate at which water must be removed from the floor of excavation in
order to prevent flooding.
Rate of flow Q= kh N f
Nd
K is the mean permeability
Nf is the number of flow tubes.
Nd is the number of equipotential drops.
From the flow net above, we obtain that Nf =6 and Nd =6
k =4∗10−5 m/ s
Substituting the values into the formula;
Q= 4∗10−5∗6∗5
5 =64∗10−5 m3 /s /m/run
c) Calculate the pore water pressure at point A just under the toe of the sheet piled
wall.
Pore water pressure uw =(h−z) γ w
Substituting the values;

GEOTECHNICAL ENGINEERING ASSIGNMENT 3
uw = ( 12− ( −4 ) ) ∗10=160 kN /m2
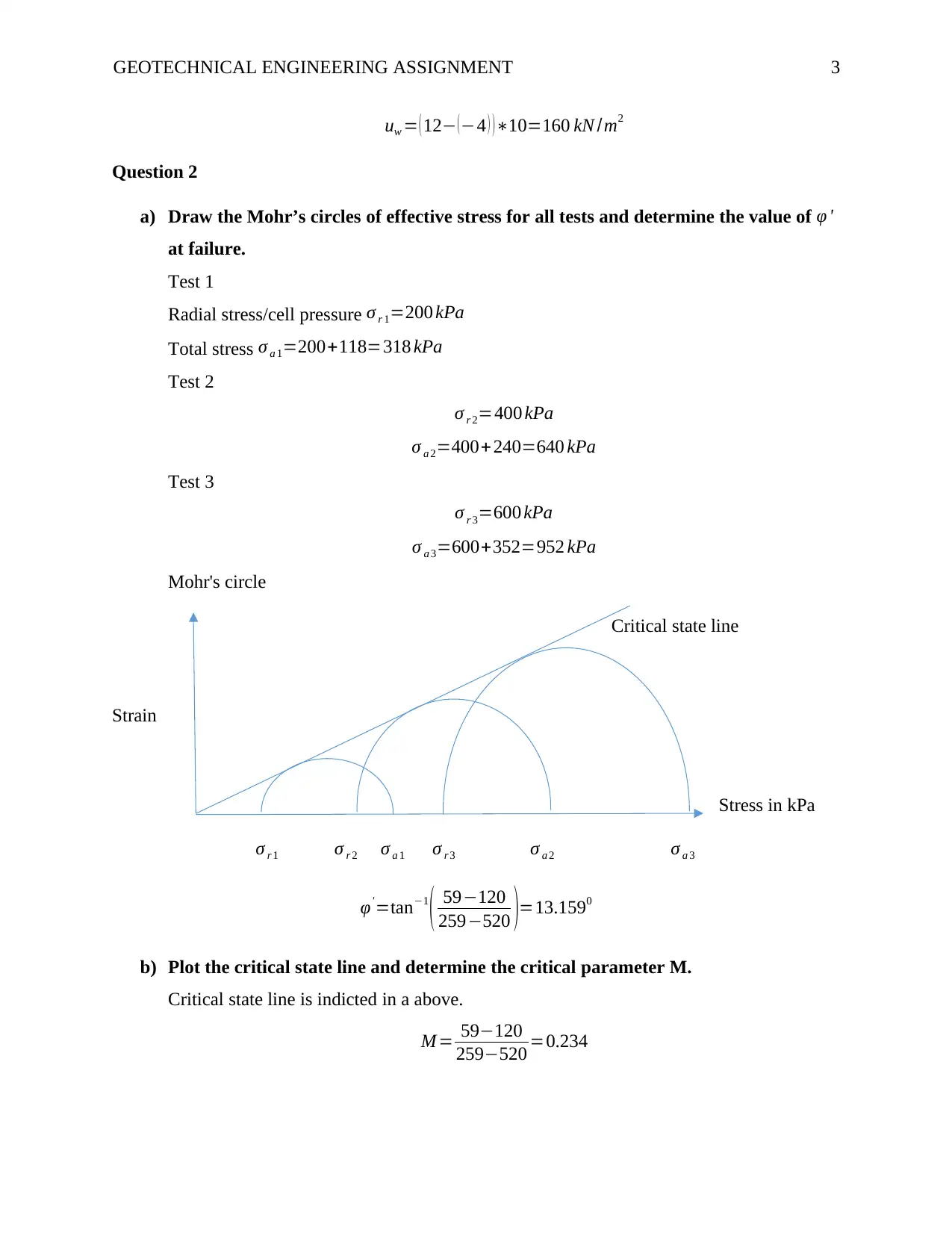
Question 2
a) Draw the Mohr’s circles of effective stress for all tests and determine the value of φ '
at failure.
Test 1
Radial stress/cell pressure σ r 1=200 kPa
Total stress σ a 1=200+118=318 kPa
Test 2
σ r 2=400 kPa
σ a 2=400+ 240=640 kPa
Test 3
σ r 3=600 kPa
σ a 3=600+352=952 kPa
Mohr's circle
Critical state line
Strain
Stress in kPa
σ r 1 σ r 2 σ a 1 σ r 3 σ a 2 σ a 3
φ'=tan−1
( 59−120
259−520 )=13.1590
b) Plot the critical state line and determine the critical parameter M.
Critical state line is indicted in a above.
M = 59−120
259−520 =0.234

GEOTECHNICAL ENGINEERING ASSIGNMENT 4
c) Would failure occur on a plane within a mass of this soil at a point where the shear
stress is 70 kPa and the vertical effective stress is 200 kPa?
Solution
We solve by comparing the critical parameter values of this case and that obtained in part
b. If the M obtained is greater than 0.234, then failure will occur.
M = 70
200 =0.35
The value of M in this case is greater than that in part b. Therefore, failure will occur.
Question 3
a) Calculate the vertical stress increase below the centre of the half of the raft
subjected to a uniform pressure of 100 kPa at a depth of 20m using Fadum’s (1948)
chart.
Solution
Uniform pressure q=100 kN /m2
Vertical stress σ z =4 q I r
I r is obtained from the Fadum chart as follows.
m= B
z =16
20 =0.8
n= L
z = 20
20 =1
Obtaining the value of I r using the values of m and n we get
I r=0.20
Substituting back the values into the formula for vertical stress we get
σ z =4∗100∗0.20=80 kN /m2
Change in vertical stress ∆ σ=P∗Ir =100∗0.20=20 kN /m2
b) Calculate the total settlement under the centre of the half of the raft that is
subjected to a uniform pressure of 100 kPa.
Solution
Total settlement S= q
E f
Where f is the settlement coefficient given by

GEOTECHNICAL ENGINEERING ASSIGNMENT 5
f =∑ Cn
2 π =
16
8 + 20
8 + 20
8
2 π = 7
2 π
Substituting back
S= 100∗7
70∗103∗2 π =0.0016 m
c) What is the main difficulty in using an elastic analysis to calculate the settlements of a
foundation? Justify your answer.
Elastic analysis determines the immediate displacement of the soil brought by overlying
weight. In reality, the soil undergoes continuous displacement throughout its life. The
elastic analysis methodology do not put into consideration future increased loadings.
Question 4
a) Define the terms overconsolidation ratio, normally consolidated and over-
consolidated soil
Overconsolidation ratio (OCR) refers to the ratio of past maximum stress to present
effective stress of the soil.
When the ratio of past maximum stress to present effective stress of the soil is equal to1,
the soil is termed as normally consolidated.
When OCR>1, the past maximum stress exceeds the present effective stress of the soil
and its termed as being over-consolidated.
b) Office building
i) Assuming the unit weight of water is 10kN/m3, calculate total and effective
stresses and pore water pressure at the centre of the clay layer.
Total stress ¿ gsand dsand +gclay dclay +gwater dwater
¿ ( 17∗3 ) + ( 18.5∗8 ) + ( 2∗20 )+ ( 10∗10 )
¿ 339 kN /m2
Effective stress ¿ total stress− pore pressure
Pore water pressure ¿ gwater dwater

GEOTECHNICAL ENGINEERING ASSIGNMENT 6
¿ 10∗10
¿ 100 kN /m2
Effective stress ¿ 339−100
¿ 239 kN /m2
ii) The clay has specific gravity (Gs) of 2.7 and water content (w) of 38%
initially. The proposed building will impose a vertical stress increase of 100
kPa at the middle of the clay layer. Assuming the coefficient of consolidation
(Cc) is 0.3, calculate the primary consolidation settlement of the clay.
Solution
Primary consolidation Sc ,1 D= Cc
1+eo
Hlog ( σ 'vf
σ 'c )
Initial effective overburden stress σ 'v ,o = ( 2∗19 ) + ( 11∗( 20−10 ) )=68 kPa
Stress increment ∆ σ=100 kPa
Final stress σ 'vf =100+68=168 kPa
σ ' c= ( 4∗20 ) + ( 10∗4 ) =120 kPa
Primary consolidation settlement Sc ,1 D= 0.3
1+0.38 ( 4 ) log ( 168
120 )=0.127 m ≈ 12.7 cm

GEOTECHNICAL ENGINEERING ASSIGNMENT 7
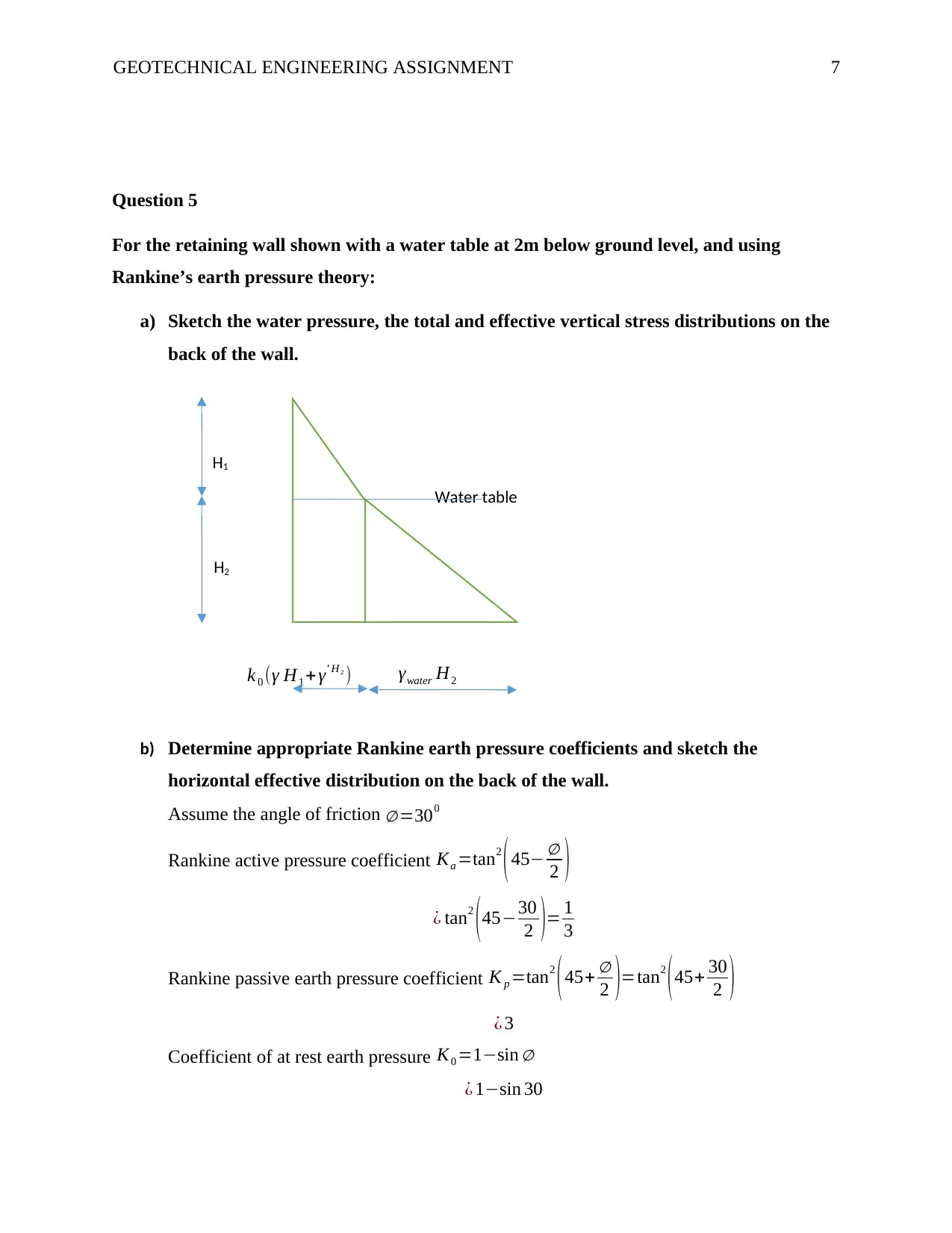
Question 5
For the retaining wall shown with a water table at 2m below ground level, and using
Rankine’s earth pressure theory:
a) Sketch the water pressure, the total and effective vertical stress distributions on the
back of the wall.
H1
Water table
H2
k 0 (γ H1 + γ' H 2
) γwater H2
b) Determine appropriate Rankine earth pressure coefficients and sketch the
horizontal effective distribution on the back of the wall.
Assume the angle of friction ∅ =300
Rankine active pressure coefficient Ka =tan2
(45− ∅
2 )
¿ tan2
(45−30
2 )= 1
3
Rankine passive earth pressure coefficient K p =tan2
(45+ ∅
2 )=tan2
(45+ 30
2 )
¿ 3
Coefficient of at rest earth pressure K0 =1−sin ∅
¿ 1−sin 30

GEOTECHNICAL ENGINEERING ASSIGNMENT 8
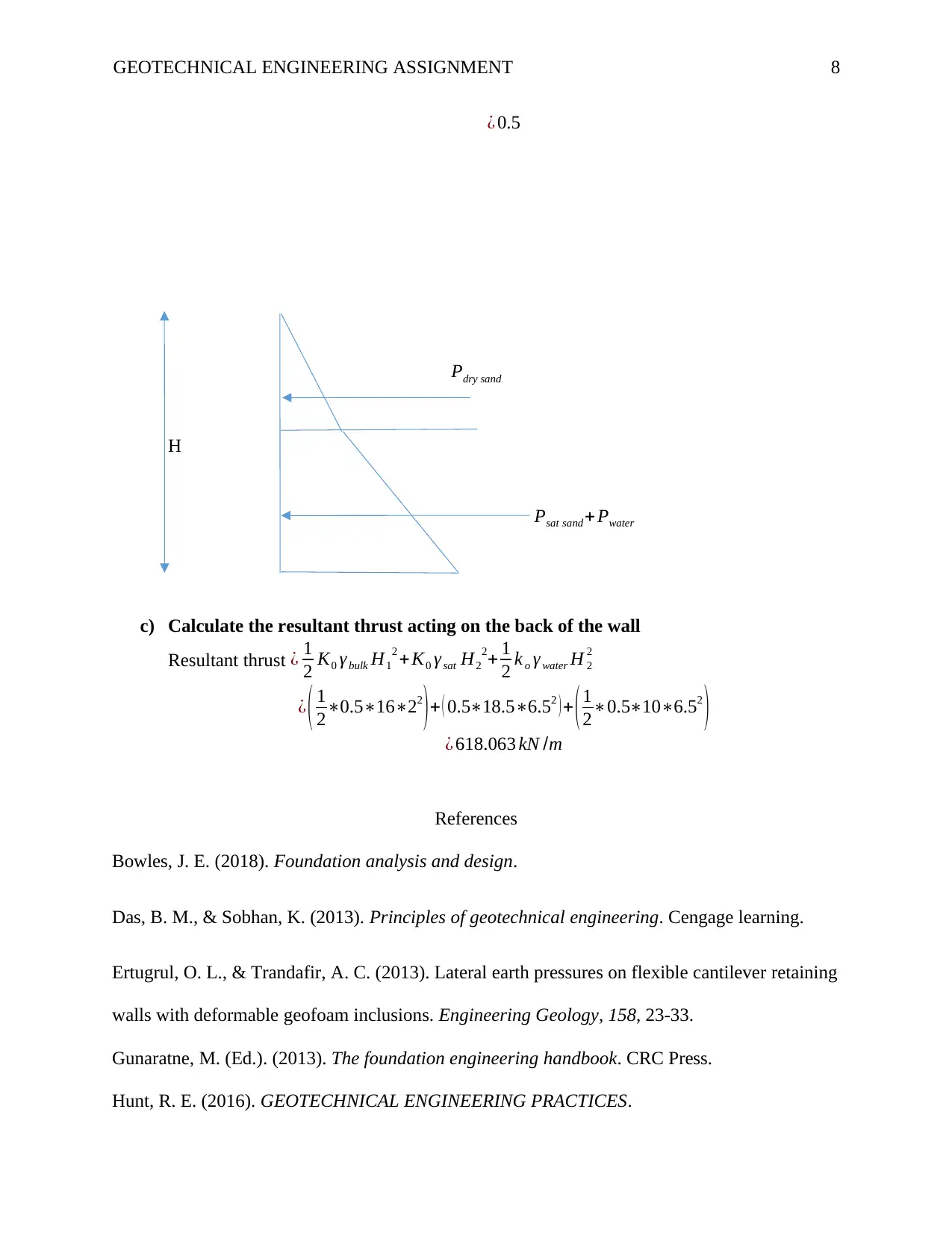
¿ 0.5
Pdry sand
H
Psat sand + Pwater
c) Calculate the resultant thrust acting on the back of the wall
Resultant thrust ¿ 1
2 K0 γ bulk H1
2 +K0 γ sat H2
2+ 1
2 k o γ water H 2
2
¿ ( 1
2∗0.5∗16∗22
)+ ( 0.5∗18.5∗6.52 ) + (1
2∗0.5∗10∗6.52
)
¿ 618.063 kN /m
References
Bowles, J. E. (2018). Foundation analysis and design.
Das, B. M., & Sobhan, K. (2013). Principles of geotechnical engineering. Cengage learning.
Ertugrul, O. L., & Trandafir, A. C. (2013). Lateral earth pressures on flexible cantilever retaining
walls with deformable geofoam inclusions. Engineering Geology, 158, 23-33.
Gunaratne, M. (Ed.). (2013). The foundation engineering handbook. CRC Press.
Hunt, R. E. (2016). GEOTECHNICAL ENGINEERING PRACTICES.

GEOTECHNICAL ENGINEERING ASSIGNMENT 9
Sitar, N., Mikola, R. G., & Candia, G. (2012). Seismically induced lateral earth pressures on
retaining structures and basement walls. In Geotechnical Engineering State of the Art and
Practice: Keynote Lectures from GeoCongress 2012 (pp. 335-358).
Towhata, I. (2010). Geotechnical earthquake engineering. Springer Science & Business Media.