GETE 1340 Technical Mathematics for Engineers I: Homework 1 Solution

This document provides a comprehensive solution to GETE 1340 Technical Mathematics for Engineers I Homework 1. The solution addresses various mathematical concepts relevant to engineering, including simplifying algebraic expressions, converting between ordinary and scientific notation, and solving for indicated parameters in equations. The assignment also includes geometry problems involving angle determination, perimeter and area calculations for various shapes like triangles, circles, and trapezoids. Furthermore, it covers surface area and volume calculations for prisms, cylinders, pyramids, and spheres. The solution also explores trigonometric functions, function evaluation, and problem-solving involving trigonometric principles, including angle conversions and the application of trigonometric functions to real-world scenarios such as calculating the height reached by a fire truck ladder. Additionally, the solution includes graphing and data analysis to determine appropriate functions and solve problems related to rates and investments, providing a complete and detailed guide to the homework assignment.

Engineering Mathematics
Student Name:
Instructor Name:
Course Number:
16th September 2019

Question #1:
a. Simplify the following expressions:
15 p4 q2 r
5 p q5 r =3 p3
q3 =3 p3 q−3
−16 N−2 ( N T 2 )
−2 N0 T−1 =8 N−2 ( N T2 ) T =8 N−1 T3
−35 x−1 y ( x2 y )
5 x y−1 =−7 x−2 y2 ( x2 y ) =−7 y3
b. Change numbers in ordinary notation to scientific notation, or vice versa:
A certain computer has 60,000,000,000,000 bytes of memory =
6.0 ×1013 bytes of memory
Police radar has a frequency of 1.02 ×109 Hz = 1,020,000,000 Hz.
c. Solve for the indicated parameter:
V =π r2 L, for L
L= V
π r2
P= π2 EI
L2 , for E
E= P L2
π2 I
Z2
(1− λ
2a )=k , for λ
Z2
( 2 a−λ
2 a )=k
2 a Z2−λ Z2
2 a =k
2 a Z2− λ Z2=2 ka
λ Z2=2 a Z2−2 ak
λ Z2=2 a ( Z2−k )
λ= 2a ( Z2−k )
Z2
λ=2 a (1− k
Z2 )
d. Fire forest
Let the distance be x mi
Time taken to travel from the fire to the pond is x mi/h
105 mi/h = x
105 h
Time taken to travel from the pond to the fire is x mi/h
70 mi/h = x
70 h

Total time taken: x
105 h+ x
70 h=0.5 h
x
105 + x
70 =0.5
2 x +3 x
210 =0.5
2 x+3 x=0.5∗210
5 x=105
x= 105
5 =21
Time taken to travel from the pond to the fire is
x mi
h
70 mi
h
= x
70 h
¿ 21
70 h= 3
10 h=0.3 h=18 minutes
Therefore it takes 18 minutes to travel from the pond to the fire.
Question #2:
a. Determine the indicated angles:
1. ¿ CGE=1800−1480=320
2. ¿ EGF=1800− ( 900+320 ) =1800 −1220=580
3. ¿ DGH=¿CGE=320
4. ¿ EGI=320 + 900=1220
b. Find the perimeter and area of the following shapes:
Triangle of sides 175 cm, 138 cm, 119 cm
P=175+ 138+ 119
¿ 432 cm
A= √ s ( s−a ) ( s−b ) ( s−c )
s= 175+138+119
2 = 432
2 =216
A= √216 (216−175 ) ( 216−138 ) (216−119 ) = √216 ( 41 ) (78 ) ( 97 )= √67,004,496
¿ 8185.63
Circle: d = 98.4 mm
P=πD =22
7 ∗98.4
¿ 309.2571
A=π r2

¿
22
7 ∗98.4
2 ∗98.4
2
¿ 7,607.7257
Trapezoid: b1=67.2 in, b2=126.7 in, h=34.2 in
We need to obtain the other sides first;
126.7−67.2
2 =29.75∈¿
a1=a2= √ 29.752 +34.22= √ 885.0625+1,169.64= √ 2054.7025=45.3288
P=a1 +a2 +b1+ b2=45.3288+ 45.3288+67.2+126.7=284.5576
A=1
2 ( b1 +b2 )∗h=1
2 ( 67.2+126.7 )∗34.2=1
2∗193.9∗34.2=3315.69 ¿2
c. Find the surface area and volume of the following objects:
Prism: base is right triangle with legs 26.0 cm and 34.0 cm, height is 14.0 cm
Surface area=2 ( lw+lh+wh )
¿ 2 ( 26∗34+26∗14+34∗14 )
¿ 2 ( 884+364 +476 )
¿ 2∗1724
¿ 3448 cm2
Volume=1
2∗b∗h∗l
¿ 1
2∗26∗14∗34
¿ 12376
2
¿ 6188 cm3
Cylinder: base radius 36.0 in., height 2.40 in.
Surface area=2 π r2 + πDh=2 ( 22
7 ∗36∗36 )+ 22
7 ∗72∗2.4=2∗4073.1429+543.0857
¿ 8146.2858 +543.0857
¿ 8689.3715 ¿2
Volume=π r 2 h
¿ 22
7 ∗36∗36∗2.4
¿ 9,775.5428 ¿3

Pyramid: base area 3850 ft2, height 125 ft
Surface area= 1
2∗3850∗125=240,625 ft2
Volume= Base area∗height
3 = 3850∗125
3 =160,416.6667 ft3
Sphere: diameter 2.21 mm
Surface area=4 π r2
¿
4∗22
7 ∗2.21
2 ∗2.21
2
¿ 15.3500 mm2
Volume= 4
3 π r3
¿
4
3 ∗22
7 ∗2.21
2 ∗2.21
2 ∗2.21
2
¿ 5.6539 mm3
d. Find the perimeter and the area of the following shapes
Figure 1:
We first obtain the hypotenuse;
l= √ b2+ ( 2 a ) 2= √ b2 +4 a2
P= √b2+4 a2+ b+ πD
¿ √ b2 + 4 a2 +b+
22
7 ∗2 a
2
¿ √b2 +4 a2 +b+ 22
7 a
¿ √ b2 + 4 a2 +b+ 3.1429 a
A= π r2
2 + 1
2 ab
¿
22
7 ∗a2
2 + 1
2∗2 a∗b
¿ 1.5714 a2+ab

¿ a (1.5714 a+b)
Figure 2:
P= 2∗1
4 πD +4 s
¿
2∗1
4 ∗22
7 ∗2 s+4 s
¿ 11
7 s +4 s
¿ 1.5714 s+ 4 s
¿ 5.5714 s
A=2∗1
4 π r2+ s∗s
¿
2∗1
4 ∗22
7 ∗s2 +s∗s
¿ 1.5714 s2 +s2
¿ 2.5714 s2
e. Solve the following problem
A=250
3 [ 220+190+530+480+320+ 510+260+350+730+560+250+ 240 ]
¿ 250
3 [ 4640 ]
¿ 386,666.6667 m2
Question #3:
a. Determine the appropriate function for the following cases:
Description Function
The radius of a circular water wave increases
at the rate of 2 m/s. Express the area of the
circle as a function of the time t (in s).
A=π r2
¿ π∗2 t∗2 t
¿ 4 π t 2
A conical sheet-metal hood is to cover an area
6 m in diameter. Find the total surface area A
of the hood as a function of its height h.
s2=32+ h2
s2=9+h2
s= √ 9+ h2
A=π r2 + πrs=π ( 3 )2+ π ( 3 ) √9+h2
9 π +3 π √ 9+h2
A person invests x dollars at 5% APR (annual
percentage rate) and y dollars at 4% APR. if
the total annual income is $2000, solve for y
as a function of x
Income for x dollars: 0.05x
Income for y dollars: 0.04y
Total income: 0.05 x+0.04 y=2000
0.04 y =2000−0.05 x

y= 2000−0.05 x
0.04
y=50,000−1.25 x
Fencing around a rectangular storage depot
area costs twice as much along the front as
along the other three sides. The back costs
$10 per foot. Express the cost C of the
fencing as a function of the width w if the
length (along the front) is 20 ft. longer than
the width.
(20+w)20+(w +w+20+ w)10=C;
400+20 w+30 w +200=C; C=50W+600
b. Evaluate the following functions:
Function Value
H ( h ) = √ 1−2h ; find H ( −4 ) ∧H ( 2 h ) +2 H (−4 )= √1−2(−4)= √1+8= √9=3∨−3
H ( 2 h ) +2= √ 1−2(2 h)+2= √ 1−4 h+2
c. Solve the following problem:
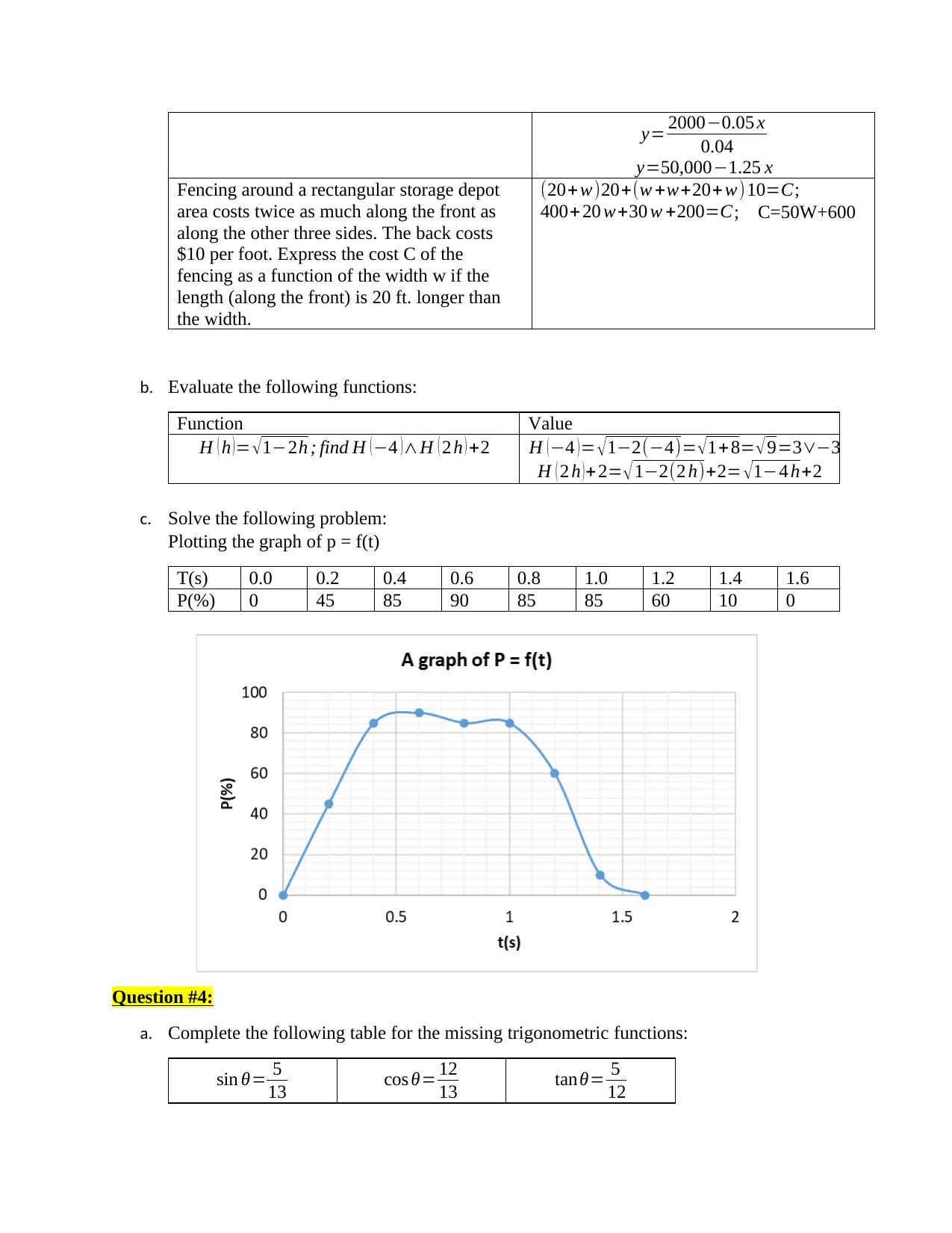
Plotting the graph of p = f(t)
T(s) 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6
P(%) 0 45 85 90 85 85 60 10 0
Question #4:
a. Complete the following table for the missing trigonometric functions:
sin θ= 5
13 cos θ= 12
13 tanθ= 5
12

cos θ= 3
8 sin θ= √55
8 tanθ= √55
3
cot θ=40 sin θ= 1
√1601 tanθ= 1
cot θ = 1
40
tan θ=2 cos θ= 1
√5 csc θ= 1
sin θ = 1
2/ √ 5 = √ 5
2
b. Explain three different ways in which the value of x can be found for the triangle shown
in this figure, which one is the easiest?
Solution
 Using angles; we apply the use of angles and one side to obtain the missing sides
 Using Pythagoras theorem; we use the adjacent, opposite and hypotenuse
formulas to obtain the missing sides
 Using sine rule; this uses the trigonometric similarities to obtain the missing sides.
The easiest is the use of angles.
c. Solve the following problem?
The base of a 75-ft fire truck ladder is at the rear of the truck and is 4.8 ft above the
ground. If the ladder is extended backward at an angle of 620 with the horizontal, how
high up on the building does it reach, and how far from the building must the back of
the truck be in order that the ladder just reach the building.
sin θ= opposite
Hypotenuse
sin 62= opposite
75
¿ 0.88294759= opposite
75
opposite=0.88294759∗75=66.2211 ft
So the total distance up is; 66.2211+4.8 ft=71.0211 ft
Next we obtain the horizontal distance
√ 752−66.22112= √ 5,625−4,385.23= √ 1,239.77=35.2104 ft
Thus the truck must be 35.2104 ft from the building.
Question #5:
a. Complete the following table for the missing trigonometric functions:
Point coordinates sin θ cos θ tanθ

(6, 8) sin θ= 8
10 cos θ= 6
10 tanθ= 6
8
(-12, 5) sin θ= 5
13 cos θ=−12
13 tanθ=−12
5
(42, -12) sin θ= −12
√1908 cos θ= 42
√1908 tanθ= 42
−12 =−7
2 =−3.5
(-2, -3) sin θ= −3
√13 cos θ= −2
√13 tanθ=−2
−3 = 2
3
b. Convert the following angles to its equivalent:
400 2520 1530 243.70 3050 67.50 -1620 100.80 -2020 741.60
0.2222π 7π/5 0.85π -1.354 1.694π 3π/8 -0.9π 0.56 1.1222π 4.12
c. Determine the value of the following trigonometric functions using calculator:
cos 265.50 sin 141.30
sin 9 π
5 sec 5 π
8
cos−162.3 tan 436.4
0.0785 0.6252 -0.5878 -2.6131 -0.9527 4.1335
d. Solve the following problems?
We first obtain AC:
AC= √ ( 402 +3 02 )
¿ √ ( 1600+900 )
¿ √ ( 2500 )
¿ 50
Perimeter=P= AB +BC +CD+ AD
CD=20∗50∗pi /180=17.45 m
P=40+30+17.45+50=137.5 m
Thus the perimeter of the land is 137.5 metres
Computing the area;
We first compute the area of the sector;
Area of the sector ACD= 1
2 r2 θ
¿ 1
2 ( AC2 ) θ
¿ 1
2
( 502 )∗20∗pi
180
¿ 1250 pi
9 =436.3 m2
Next we compute the area of the triangle;

Area=1
2 b∗h
¿ 1
2∗30∗40
¿ 1200
2
¿ 600 m2
Total area: 600 m2+436.3 m2=1036.3 m2