NUS Chemical Engineering: Gibbs Free Energy of Nanoputian at 500 K
VerifiedAdded on 2022/05/06
|9
|3165
|36
Homework Assignment
AI Summary
This report details the calculation of the overall Gibbs free energy of a nanoputian molecule at 500 K, as part of a Chemical Engineering assignment at the National University of Singapore (NUS). The study employs global optimization and thermodynamic potential calculations to determine the Gibbs free energies for each local minima of the molecule. The methodology involves local and global optimization using the BrennerPotential and minima hopping algorithm, molecular vibrations calculation, and the utilization of ASE modules in Python for thermodynamic potential calculations. The results include the molecular structure of the nanoputian, plots of Gibbs free energies for each minima, and the overall Gibbs energy calculation using an iterative approach based on the partition function and free energy formula. The analysis includes comparisons with calculated isomer energies and a discussion of the validity of thermodynamic theories. The assignment aims to determine the overall Gibbs energy and compare it with the energy of calculated isomers. The report covers the methodology, results, and discussions, including the use of Python code and ASE modules.

National University of Singapore (NUS)
Department of Chemical & Biomolecular Engineering
CN5002: Advanced Reaction Engineering
Master of Science in Chemical Engineering
AY 2020/21 Semester 2
Week 4 Homework Assignment 2 Written Report
Title: Gibbs Free Energy of Nanoputian Molecule at 500 K
Student Name: Abdul Hannan Bin Abdul Rahman
Student Matriculation Number: A0229546W
Lecturer Name: Assistant Professor Sergey Kozlov
Department of Chemical & Biomolecular Engineering
CN5002: Advanced Reaction Engineering
Master of Science in Chemical Engineering
AY 2020/21 Semester 2
Week 4 Homework Assignment 2 Written Report
Title: Gibbs Free Energy of Nanoputian Molecule at 500 K
Student Name: Abdul Hannan Bin Abdul Rahman
Student Matriculation Number: A0229546W
Lecturer Name: Assistant Professor Sergey Kozlov
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Page 1 of 8
Abstract
Both global optimization and thermodynamic potentials calculations were employed in
this assignment in order to determine the Gibbs free energies for each local minima of the
nanoputian molecule at a system temperature of 500 K. The aim of this assignment is to
calculate the overall Gibbs energy of the molecule upon combining and incorporating all
the values of Gibbs free energies of each local minima into overall Gibbs energy equation
(equation 1), derived from the partition function and free energy formula. While working
on this assignment, several functions were imported from atomic simulation environment
(ASE) modules which were installed onto our Google Colab notebook. These functions
were then utilised, along with several Python codings, in order to determine the overall
Gibbs free energy of our molecule while at the same time, fulfilling the objectives of this
assignment. The result obtained for the overall Gibbs energy will then later be compared
with the energies of calculated isomers for further analysis at the end of this assignment.
1. Aim and Objectives
Aim: To calculate the overall Gibbs energy of the nanoputian molecule at a system
temperature of 500 K.
Objectives:
▪ Structure of nanoputian molecule will be locally optimized until forces on atoms reach
0.01 unit eV/Angstrom.
▪ Structure of the nanoputian will be globally optimized at specific values of temperature
and length of molecular dynamics (MD) simulations before generating the local minima
of the molecule.
▪ Molecular vibrations calculation of the nanoputian molecule will be performed before
displaying the summary list of molecular vibrational frequencies and energies.
▪ Thermodynamic potentials of nanoputian molecule will be calculated upon specifying
all the necessary parameters for thermodynamics calculation.
▪ Gibbs free energies for each of the ten local minima of the nanoputian molecule will
be calculated at a system temperature of 500 K.
▪ Overall Gibbs energy of the nanoputian molecule will be iteratively calculated using a
loop within the overall Gibbs energy equation (equation 1).
Abstract
Both global optimization and thermodynamic potentials calculations were employed in
this assignment in order to determine the Gibbs free energies for each local minima of the
nanoputian molecule at a system temperature of 500 K. The aim of this assignment is to
calculate the overall Gibbs energy of the molecule upon combining and incorporating all
the values of Gibbs free energies of each local minima into overall Gibbs energy equation
(equation 1), derived from the partition function and free energy formula. While working
on this assignment, several functions were imported from atomic simulation environment
(ASE) modules which were installed onto our Google Colab notebook. These functions
were then utilised, along with several Python codings, in order to determine the overall
Gibbs free energy of our molecule while at the same time, fulfilling the objectives of this
assignment. The result obtained for the overall Gibbs energy will then later be compared
with the energies of calculated isomers for further analysis at the end of this assignment.
1. Aim and Objectives
Aim: To calculate the overall Gibbs energy of the nanoputian molecule at a system
temperature of 500 K.
Objectives:
▪ Structure of nanoputian molecule will be locally optimized until forces on atoms reach
0.01 unit eV/Angstrom.
▪ Structure of the nanoputian will be globally optimized at specific values of temperature
and length of molecular dynamics (MD) simulations before generating the local minima
of the molecule.
▪ Molecular vibrations calculation of the nanoputian molecule will be performed before
displaying the summary list of molecular vibrational frequencies and energies.
▪ Thermodynamic potentials of nanoputian molecule will be calculated upon specifying
all the necessary parameters for thermodynamics calculation.
▪ Gibbs free energies for each of the ten local minima of the nanoputian molecule will
be calculated at a system temperature of 500 K.
▪ Overall Gibbs energy of the nanoputian molecule will be iteratively calculated using a
loop within the overall Gibbs energy equation (equation 1).

Page 2 of 8
2. Methodology
This assignment focuses solely on the nanaputian compound as the subject material for
studying the thermodynamic property. A right methodological approach is needed that will
allow us to determine the value of overall Gibbs free energy of this compound. This section
describes the overall methodology and procedures used to achieve the aim and objectives
of our assignment. The procedures involved performing an optimization on the nanoputian
molecule, calculating the thermodynamic potentials (Gibbs free energies) for each of the
local minima generated and finally, determining the overall Gibbs free energy of molecule.
These work procedures were carried out in our Google Colab Notebook, involving the use
of several Python codings and some useful functions imported from the ASE modules.
The assignment work started off with setting up of the nanoputian model in order to assign
the right calculator to the nanoputian molecule and plot its molecular structure using both
the ‘BrennerPotential’ and ‘plot_atoms’ functions respectively. A local optimization was
performed on the molecule as a try-out using the BFGS algorithm to determine the lowest
potential energy of the molecule at which forces on atoms (fmax) reach 0.01 eV/Angstrom.
Afterwards, a global optimization on the nanoputian molecule was then eventually carried
out in order to generate a total of ten local minima and find the lowest potential energy
among the ten local minima. Two global optimization methods are available for use which
include both the basin hopping and minima hopping [1]. For our assignment, we have opted
to choose minima hopping algorithm as it is convenient and requires less time to perform
MD simulation. In this assignment, our global optimization procedure was performed at a
specific high temperature of 2000 K, length of MD simulations of 15 and a repeated total
of 10 steps to generate ten local minima as a result.
In order to determine the values of Gibbs free energies for each of the ten local minima of
the molecule, a thermodynamic potentials calculation is required to be performed first using
‘IdealGasThermo’ function which can be imported from the ase.thermochemistry module.
Several key parameters must be specified before performing the thermodynamic potentials
calculation. These include the list of positive vibrational energies obtained from the results
of our molecular vibrations calculations, electronic energy for the structure in local minima,
which can be obtained using the get_potential_energy method, zero value for spin number
as nanoputians are regarded as closed-shell molecules, two value for the symmetry number
and lastly, specifying the molecular geometry as ‘non-linear’. Thus, this will complete the
2. Methodology
This assignment focuses solely on the nanaputian compound as the subject material for
studying the thermodynamic property. A right methodological approach is needed that will
allow us to determine the value of overall Gibbs free energy of this compound. This section
describes the overall methodology and procedures used to achieve the aim and objectives
of our assignment. The procedures involved performing an optimization on the nanoputian
molecule, calculating the thermodynamic potentials (Gibbs free energies) for each of the
local minima generated and finally, determining the overall Gibbs free energy of molecule.
These work procedures were carried out in our Google Colab Notebook, involving the use
of several Python codings and some useful functions imported from the ASE modules.
The assignment work started off with setting up of the nanoputian model in order to assign
the right calculator to the nanoputian molecule and plot its molecular structure using both
the ‘BrennerPotential’ and ‘plot_atoms’ functions respectively. A local optimization was
performed on the molecule as a try-out using the BFGS algorithm to determine the lowest
potential energy of the molecule at which forces on atoms (fmax) reach 0.01 eV/Angstrom.
Afterwards, a global optimization on the nanoputian molecule was then eventually carried
out in order to generate a total of ten local minima and find the lowest potential energy
among the ten local minima. Two global optimization methods are available for use which
include both the basin hopping and minima hopping [1]. For our assignment, we have opted
to choose minima hopping algorithm as it is convenient and requires less time to perform
MD simulation. In this assignment, our global optimization procedure was performed at a
specific high temperature of 2000 K, length of MD simulations of 15 and a repeated total
of 10 steps to generate ten local minima as a result.
In order to determine the values of Gibbs free energies for each of the ten local minima of
the molecule, a thermodynamic potentials calculation is required to be performed first using
‘IdealGasThermo’ function which can be imported from the ase.thermochemistry module.
Several key parameters must be specified before performing the thermodynamic potentials
calculation. These include the list of positive vibrational energies obtained from the results
of our molecular vibrations calculations, electronic energy for the structure in local minima,
which can be obtained using the get_potential_energy method, zero value for spin number
as nanoputians are regarded as closed-shell molecules, two value for the symmetry number
and lastly, specifying the molecular geometry as ‘non-linear’. Thus, this will complete the
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Page 3 of 8
thermo function for our assignment. The Gibbs free energies for each of the local minima
generated can be calculated by incorporating the get_gibbs_energy method into the thermo
function in our Python code lines, with the system temperature taken as 500 K and pressure
as 1 Bar. The values of the Gibbs free energies for each local minima can then be plotted
in a graph using matplotlib.pyplot function. Next using the right Python codings, the list of
Gibbs free energies values will each be rounded to three digits to remove any duplicated
entry in order to ensure the validity of our thermodynamic analysis.
The final stage of this assignment work requires the calculation of the overall Gibbs free
energy iteratively using a loop within the overall Gibbs energy equation (see equation 1
below), which was derived from both the partition function and free energy formula [2].
Equation 1: Overall Gibbs Free Energy Equation [2]
In order to calculate overall Gibbs energy, the temperature (T) value in this assignment was
taken the same as 500 K previously and will then be multiplied with the value of Boltzmann
constant (k), imported from the ase.units module. In addition to that, both the logarithmic
and exponential functions were also imported from the numpy module to prepare for our
overall energy calculation. Finally, the delta (∆) value above was set as -376.9 eV for easy
exponential computation of the overall Gibbs energy equation and to avoid any overflow
error massage while working on the assignment. Upon setting delta (∆) value, the overall
Gibbs energy of nanoputian molecule can then be iteratively calculated using our equation
1 above, along with the right Python codings. The Python codings used for this calculation
can be found in our ‘w4_homework[1]_5020_clean.py’ file. In this assignment, the value
of iterations (i) was chosen in the same length as that of the Gibbs energy, similarly to the
total number of local minima generated which was calculated around ten in total. While
performing the overall Gibbs calculation halfway, a statistical method of thermodynamic
calculation was also employed using the ‘statistics.mean’ function to calculate the mean
value of our calculated free energies (Q_cal) [3]. Inserting this mean value into the square
bracket in equation 1 above, the overall Gibbs energy can then finally be calculated. The
value obtained for this overall Gibbs free energy will then be recorded in our Google Colab
notebook and later will be compared with the Gibbs free energy values of our calculated
isomers to observe the numerical differences (obs_diff) between them for further analysis.
thermo function for our assignment. The Gibbs free energies for each of the local minima
generated can be calculated by incorporating the get_gibbs_energy method into the thermo
function in our Python code lines, with the system temperature taken as 500 K and pressure
as 1 Bar. The values of the Gibbs free energies for each local minima can then be plotted
in a graph using matplotlib.pyplot function. Next using the right Python codings, the list of
Gibbs free energies values will each be rounded to three digits to remove any duplicated
entry in order to ensure the validity of our thermodynamic analysis.
The final stage of this assignment work requires the calculation of the overall Gibbs free
energy iteratively using a loop within the overall Gibbs energy equation (see equation 1
below), which was derived from both the partition function and free energy formula [2].
Equation 1: Overall Gibbs Free Energy Equation [2]
In order to calculate overall Gibbs energy, the temperature (T) value in this assignment was
taken the same as 500 K previously and will then be multiplied with the value of Boltzmann
constant (k), imported from the ase.units module. In addition to that, both the logarithmic
and exponential functions were also imported from the numpy module to prepare for our
overall energy calculation. Finally, the delta (∆) value above was set as -376.9 eV for easy
exponential computation of the overall Gibbs energy equation and to avoid any overflow
error massage while working on the assignment. Upon setting delta (∆) value, the overall
Gibbs energy of nanoputian molecule can then be iteratively calculated using our equation
1 above, along with the right Python codings. The Python codings used for this calculation
can be found in our ‘w4_homework[1]_5020_clean.py’ file. In this assignment, the value
of iterations (i) was chosen in the same length as that of the Gibbs energy, similarly to the
total number of local minima generated which was calculated around ten in total. While
performing the overall Gibbs calculation halfway, a statistical method of thermodynamic
calculation was also employed using the ‘statistics.mean’ function to calculate the mean
value of our calculated free energies (Q_cal) [3]. Inserting this mean value into the square
bracket in equation 1 above, the overall Gibbs energy can then finally be calculated. The
value obtained for this overall Gibbs free energy will then be recorded in our Google Colab
notebook and later will be compared with the Gibbs free energy values of our calculated
isomers to observe the numerical differences (obs_diff) between them for further analysis.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
Page 4 of 8
Theoretically, it is expected that the value of overall Gibbs energy to be much lower than
or the same as the lowest value of the Gibbs free energies among all the local minima. This
is because the overall value, which is also regarded as the global minima value, would not
get much higher than all the values at the local minima points [4]. The results obtained in
this assignment will allow us to verify the validity of the theory above.
3. Results and Discussion
The results of our assignment work will be presented and discussed in this section. Here is
where we will analyse the result of our local optimization, examine the potential and Gibbs
free energies for each local minima, compare the difference between overall Gibbs energy
of the nanokid with the free energies of calculated isomers (obs_diff), and also observe and
comment on the figures plotted in our Google Colab notebook. The following figures below
were plotted and obtained as our results:
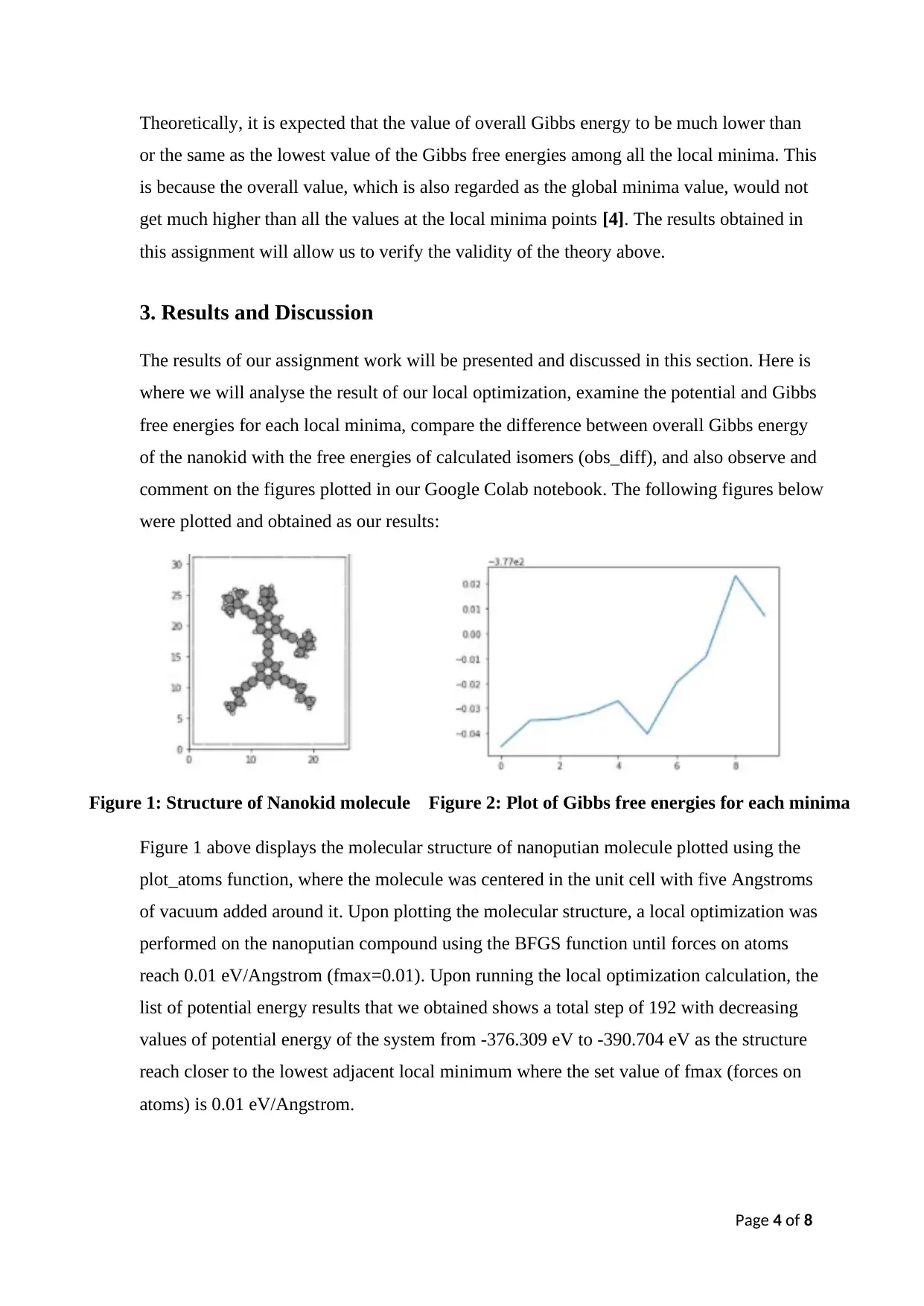
Figure 1: Structure of Nanokid molecule Figure 2: Plot of Gibbs free energies for each minima
Figure 1 above displays the molecular structure of nanoputian molecule plotted using the
plot_atoms function, where the molecule was centered in the unit cell with five Angstroms
of vacuum added around it. Upon plotting the molecular structure, a local optimization was
performed on the nanoputian compound using the BFGS function until forces on atoms
reach 0.01 eV/Angstrom (fmax=0.01). Upon running the local optimization calculation, the
list of potential energy results that we obtained shows a total step of 192 with decreasing
values of potential energy of the system from -376.309 eV to -390.704 eV as the structure
reach closer to the lowest adjacent local minimum where the set value of fmax (forces on
atoms) is 0.01 eV/Angstrom.
Theoretically, it is expected that the value of overall Gibbs energy to be much lower than
or the same as the lowest value of the Gibbs free energies among all the local minima. This
is because the overall value, which is also regarded as the global minima value, would not
get much higher than all the values at the local minima points [4]. The results obtained in
this assignment will allow us to verify the validity of the theory above.
3. Results and Discussion
The results of our assignment work will be presented and discussed in this section. Here is
where we will analyse the result of our local optimization, examine the potential and Gibbs
free energies for each local minima, compare the difference between overall Gibbs energy
of the nanokid with the free energies of calculated isomers (obs_diff), and also observe and
comment on the figures plotted in our Google Colab notebook. The following figures below
were plotted and obtained as our results:
Figure 1: Structure of Nanokid molecule Figure 2: Plot of Gibbs free energies for each minima
Figure 1 above displays the molecular structure of nanoputian molecule plotted using the
plot_atoms function, where the molecule was centered in the unit cell with five Angstroms
of vacuum added around it. Upon plotting the molecular structure, a local optimization was
performed on the nanoputian compound using the BFGS function until forces on atoms
reach 0.01 eV/Angstrom (fmax=0.01). Upon running the local optimization calculation, the
list of potential energy results that we obtained shows a total step of 192 with decreasing
values of potential energy of the system from -376.309 eV to -390.704 eV as the structure
reach closer to the lowest adjacent local minimum where the set value of fmax (forces on
atoms) is 0.01 eV/Angstrom.

Page 5 of 8
Using the minima hopping algorithm, global optimization was then performed on nanokid
molecule in order to generate ten local minima for the molecule and also find the lowest
potential energy among these ten local minima. The potential energies of structure from
‘minima.traj’ file, which was generated by our global optimization, can be calculated using
BrennerPotential function and get_potential_energy method. Upon running the Python
code cell, the list of potential energies values for each local minima was obtained as a result
Our result gave us varying potential energy values ranging from -390.704 to -390.635 eV.
Thus, the lowest recorded potential energy of the system is -390.704 eV, which occurs at
the 1st local minima point.
Prior to performing thermodynamic potential calculation, molecular vibrations calculation
was performed beforehand using vibrations function and then, the results of our molecular
vibrational energies will be summarized using the summary method. Upon running the code
cell, our vibrational summary result shows a total of 15 imaginary vibration energies, each
with a unit of eV. Using right Python codings, these imaginary vibrational energies should
then be removed from our vibrational summary list as they should not be accounted for the
thermodynamic potentials calculation. Upon specifying all the key parameters necessary
for the thermo function, the Gibbs free energies for each of the ten local minima generated
can then be calculated using the right Python codings and some useful functions with the
system temperature taken as 500 K and pressure as 1 Bar. The Python codings used for this
calculation can be found in our ‘w4_homework[1]_5020_clean.py’ file
The result of the Gibbs free energies gave us a total of 10 Gibbs free energies for each local
minima at a range of values of -377.045 to -376.977 eV. Figure 2 on page 4 shows that the
values of Gibbs free energies of the calculated isomers varying from one local minima to
another. It is observed that the lowest value of local minima was recorded to be at -377.045
eV, which occurs at the 1 st local minima point, while the highest Gibbs free energy was
found at -376.977 eV, located at 9 th local minima point. Next using right Python codings,
any duplicated entry of our Gibbs free energies should then be removed in order for our
thermodynamic analysis to be valid. From the result that we obtained, we have a total of
ten Gibbs free energies of distinct conformers and thus, none of our Gibbs free energy
(Gmin) values for each local minima were observed to differ from one another by less than
0.001 eV [2].
Using the minima hopping algorithm, global optimization was then performed on nanokid
molecule in order to generate ten local minima for the molecule and also find the lowest
potential energy among these ten local minima. The potential energies of structure from
‘minima.traj’ file, which was generated by our global optimization, can be calculated using
BrennerPotential function and get_potential_energy method. Upon running the Python
code cell, the list of potential energies values for each local minima was obtained as a result
Our result gave us varying potential energy values ranging from -390.704 to -390.635 eV.
Thus, the lowest recorded potential energy of the system is -390.704 eV, which occurs at
the 1st local minima point.
Prior to performing thermodynamic potential calculation, molecular vibrations calculation
was performed beforehand using vibrations function and then, the results of our molecular
vibrational energies will be summarized using the summary method. Upon running the code
cell, our vibrational summary result shows a total of 15 imaginary vibration energies, each
with a unit of eV. Using right Python codings, these imaginary vibrational energies should
then be removed from our vibrational summary list as they should not be accounted for the
thermodynamic potentials calculation. Upon specifying all the key parameters necessary
for the thermo function, the Gibbs free energies for each of the ten local minima generated
can then be calculated using the right Python codings and some useful functions with the
system temperature taken as 500 K and pressure as 1 Bar. The Python codings used for this
calculation can be found in our ‘w4_homework[1]_5020_clean.py’ file
The result of the Gibbs free energies gave us a total of 10 Gibbs free energies for each local
minima at a range of values of -377.045 to -376.977 eV. Figure 2 on page 4 shows that the
values of Gibbs free energies of the calculated isomers varying from one local minima to
another. It is observed that the lowest value of local minima was recorded to be at -377.045
eV, which occurs at the 1 st local minima point, while the highest Gibbs free energy was
found at -376.977 eV, located at 9 th local minima point. Next using right Python codings,
any duplicated entry of our Gibbs free energies should then be removed in order for our
thermodynamic analysis to be valid. From the result that we obtained, we have a total of
ten Gibbs free energies of distinct conformers and thus, none of our Gibbs free energy
(Gmin) values for each local minima were observed to differ from one another by less than
0.001 eV [2].
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

Page 6 of 8
The final stage of the assignment requires the calculation of overall Gibbs energy iteratively
using a loop within overall Gibbs energy equation (see equation 1 on page 3), with system
temperature taken as 500 K and delta (∆) value taken as -376.9 eV. The Gibbs free energies
of each of ten local minima was combined and incorporated into our equation 1. In addition
to that, a statistical method of thermodynamic calculation was also employed to calculate
the mean value of our calculated free energies (Q_cal) before the overall Gibbs energy can
finally be determined. Using the equation 1, the value of our overall Gibbs free energy of
nanoputian molecule can then be calculated and this was recorded as -377.106 eV using
the print function. The value is then compared with the Gibbs free energies of the calculated
isomers for further analysis on the results that we obtained.
Comparing the differences between the overall Gibbs free energy and Gibbs free energies
of calculated isomers (obs_diff), it is observed that the overall Gibbs free energy of the
nanoputian molecule is much lower than Gibbs free energies of calculated isomers with the
minimum difference in values found to be at around 0.061 eV. Thus, this strongly supports
our theory on page 4, which states that the overall Gibbs free energy value, also regarded
as the global minima value, would not get much higher than all energy values at the local
minima points. Despite being lower in values than all the energies of the local minima, the
overall Gibbs energy was not able to reach the same energy as the lowest energy value
among the local minima, which is at -377.045 eV, in order to ensure a zero difference in
value. Possible causes of this could be due to the instability in system pressure and other
parameters. Other causes could also be due to our delta (∆), as the value selected for delta
(∆) plays a big role in manipulating the differences in values between overall Gibbs energy
and free energies of calculated isomers (obs_diff), and last but not least, there might also
be some slight errors in our use of Python codes. Thus, causing the slight deviation from
the expected result of having a zero difference in value. However, it can be argued that the
result for our value difference in Gibbs free energy (obs_diff) is not that extremely high as
any difference of less than 0.1 eV can be considered to be slightly close to being accurate
and thus, may assume to be insignificant. From this, we can then make a final conclusion
statement on our final calculated result.
The final stage of the assignment requires the calculation of overall Gibbs energy iteratively
using a loop within overall Gibbs energy equation (see equation 1 on page 3), with system
temperature taken as 500 K and delta (∆) value taken as -376.9 eV. The Gibbs free energies
of each of ten local minima was combined and incorporated into our equation 1. In addition
to that, a statistical method of thermodynamic calculation was also employed to calculate
the mean value of our calculated free energies (Q_cal) before the overall Gibbs energy can
finally be determined. Using the equation 1, the value of our overall Gibbs free energy of
nanoputian molecule can then be calculated and this was recorded as -377.106 eV using
the print function. The value is then compared with the Gibbs free energies of the calculated
isomers for further analysis on the results that we obtained.
Comparing the differences between the overall Gibbs free energy and Gibbs free energies
of calculated isomers (obs_diff), it is observed that the overall Gibbs free energy of the
nanoputian molecule is much lower than Gibbs free energies of calculated isomers with the
minimum difference in values found to be at around 0.061 eV. Thus, this strongly supports
our theory on page 4, which states that the overall Gibbs free energy value, also regarded
as the global minima value, would not get much higher than all energy values at the local
minima points. Despite being lower in values than all the energies of the local minima, the
overall Gibbs energy was not able to reach the same energy as the lowest energy value
among the local minima, which is at -377.045 eV, in order to ensure a zero difference in
value. Possible causes of this could be due to the instability in system pressure and other
parameters. Other causes could also be due to our delta (∆), as the value selected for delta
(∆) plays a big role in manipulating the differences in values between overall Gibbs energy
and free energies of calculated isomers (obs_diff), and last but not least, there might also
be some slight errors in our use of Python codes. Thus, causing the slight deviation from
the expected result of having a zero difference in value. However, it can be argued that the
result for our value difference in Gibbs free energy (obs_diff) is not that extremely high as
any difference of less than 0.1 eV can be considered to be slightly close to being accurate
and thus, may assume to be insignificant. From this, we can then make a final conclusion
statement on our final calculated result.
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Page 7 of 8
4. Conclusion
In conclusion, we have finally met the aim and objectives of our assignment work. In order
to obtain an accurate result, a right methodological approach is needed that will allow us to
determine the value of our overall Gibbs energy of nanoputian molecule at a temperature
of 500 K and compare this with the Gibbs free energies of the calculated isomers for further
analysis on the value differences between them (obs_diff). Upon performing optimization
calculations on the nanokid molecule, in addition to the molecular vibrations calculation as
well as thermodynamic potentials calculation, we can then calculate the Gibbs free energies
for each of the ten local minima of the nanoputian molecule. Combining and incorporating
these free energies into our overall Gibbs energy equation (see equation 1 on page 3), in
addition to using a statistical method of thermodynamic calculation as well as few several
Python codings, the overall Gibbs free energy of our molecule was then finally determined.
Theoretically, it is expected that the overall Gibbs energy will be much lower than or the
same as the lowest value of the free energies among all the ten local minima (see our theory
on page 4). Comparing the value differences between the overall Gibbs free energy and the
Gibbs free energies of calculated isomers (see figure 2 on page 4), it is observed that the
overall Gibbs free energy of the nanoputian molecule is much lower in value than the free
energies of the calculated isomers. This difference in value could be due to several possible
reasons as identified earlier in the discussion section. Despite the fact that it was not able
to reach almost exactly the same as the lowest Gibbs energy value among all local minima
in order to ensure a zero difference in value, we have deemed the calculated result for our
overall Gibbs energy to be slightly close to being accurate enough. Hence from this, we
conclude that the result that we obtained confirms and supports the theory stated above.
However, for better accuracy, in order to minimize the difference in value between them
(obs_diff), it is highly recommended that we carry out this assignment work for a few times
and instead use the average values of the multiple results that we obtained for the overall
Gibbs free energy and energies of the calculated isomers. In addition to that, the value for
our delta (∆) needs to be readjusted regularly while calculating the overall Gibbs energy in
order to ensure that the observed difference in value (obs_diff) between the overall Gibbs
free energy and energies of the calculated isomers can be further minimized as a result,
until it reaches close to a zero value.
4. Conclusion
In conclusion, we have finally met the aim and objectives of our assignment work. In order
to obtain an accurate result, a right methodological approach is needed that will allow us to
determine the value of our overall Gibbs energy of nanoputian molecule at a temperature
of 500 K and compare this with the Gibbs free energies of the calculated isomers for further
analysis on the value differences between them (obs_diff). Upon performing optimization
calculations on the nanokid molecule, in addition to the molecular vibrations calculation as
well as thermodynamic potentials calculation, we can then calculate the Gibbs free energies
for each of the ten local minima of the nanoputian molecule. Combining and incorporating
these free energies into our overall Gibbs energy equation (see equation 1 on page 3), in
addition to using a statistical method of thermodynamic calculation as well as few several
Python codings, the overall Gibbs free energy of our molecule was then finally determined.
Theoretically, it is expected that the overall Gibbs energy will be much lower than or the
same as the lowest value of the free energies among all the ten local minima (see our theory
on page 4). Comparing the value differences between the overall Gibbs free energy and the
Gibbs free energies of calculated isomers (see figure 2 on page 4), it is observed that the
overall Gibbs free energy of the nanoputian molecule is much lower in value than the free
energies of the calculated isomers. This difference in value could be due to several possible
reasons as identified earlier in the discussion section. Despite the fact that it was not able
to reach almost exactly the same as the lowest Gibbs energy value among all local minima
in order to ensure a zero difference in value, we have deemed the calculated result for our
overall Gibbs energy to be slightly close to being accurate enough. Hence from this, we
conclude that the result that we obtained confirms and supports the theory stated above.
However, for better accuracy, in order to minimize the difference in value between them
(obs_diff), it is highly recommended that we carry out this assignment work for a few times
and instead use the average values of the multiple results that we obtained for the overall
Gibbs free energy and energies of the calculated isomers. In addition to that, the value for
our delta (∆) needs to be readjusted regularly while calculating the overall Gibbs energy in
order to ensure that the observed difference in value (obs_diff) between the overall Gibbs
free energy and energies of the calculated isomers can be further minimized as a result,
until it reaches close to a zero value.

Page 8 of 8
References
1. https://wiki.fysik.dtu.dk/ase/ase/optimize.html
2. https://colab.research.google.com/drive/1yVEmH5t0pqtiULK3PBOtGA-Wpd2b67IV
3. https://farside.ph.utexas.edu/teaching/sm1/Thermal.pdf
4. https://www.datasciencecentral.com/profiles/blogs/optimization-techniques-finding-
maxima-and-minima
References
1. https://wiki.fysik.dtu.dk/ase/ase/optimize.html
2. https://colab.research.google.com/drive/1yVEmH5t0pqtiULK3PBOtGA-Wpd2b67IV
3. https://farside.ph.utexas.edu/teaching/sm1/Thermal.pdf
4. https://www.datasciencecentral.com/profiles/blogs/optimization-techniques-finding-
maxima-and-minima
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 9
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2025 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.

