Decision Modelling: Cunningham Holdings Golf Resort Case Study
VerifiedAdded on 2023/04/04
|17
|3520
|422
Case Study
AI Summary
This case study delves into Cunningham Holdings Limited's project to construct an international golf resort, examining the strategic decisions involved in optimizing the resort's design and features. The report identifies key decision variables, including the number and type of golf holes and the choice between a standard or exclusive clubhouse. It formulates mathematical models to maximize the enjoyment index derived from the resort while adhering to resource constraints and minimum feature requirements for an international golf resort. The models consider various options, including the management's standard clubhouse plan, the shareholders' request for an exclusive clubhouse, and alternative configurations aimed at improving the project's overall value. The analysis uses data from an international survey of golfers to inform utility maximization criteria and provides a comprehensive assessment to guide the managers in making informed decisions about the golf resort's construction.

Construction of Golf Resort - A Report on Cunningham Holdings Limited
~ 1 ~
~ 1 ~
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

Part 1
Action Plan
I. Identification of the decision variables
The decision variables under the Cunningham golf resort project are the number of
golf holes to be constructed and the nature of the clubhouse to be constructed.
Let this be represented by the variables as indicated below.
x1 ; Straight par 5
x2 ; Dogleg par 5
x3 : Straight par 4
x4 : Dogleg par 4
x5 : Long par 3
x6 : Short Par 3
y ; Standrad clubhouse
w ; Exclusive clubhouse
II. Identification of the objective function
The objective pf the models is to maximise the total enjoyment index derived rom the
golf holes and the clubhouse.
III. Identification of the constraints
The constraints of the task are grouped into two; frost we have the resource constraint
which include the total land area to be covered by the project ad the total project cost.
Second set of constraint consists of the minimum features that an international golf
resort should have.
IV. Writing the objective function and the constraints as mathematical equations
i. The standard clubhouse model
~ 2 ~
Action Plan
I. Identification of the decision variables
The decision variables under the Cunningham golf resort project are the number of
golf holes to be constructed and the nature of the clubhouse to be constructed.
Let this be represented by the variables as indicated below.
x1 ; Straight par 5
x2 ; Dogleg par 5
x3 : Straight par 4
x4 : Dogleg par 4
x5 : Long par 3
x6 : Short Par 3
y ; Standrad clubhouse
w ; Exclusive clubhouse
II. Identification of the objective function
The objective pf the models is to maximise the total enjoyment index derived rom the
golf holes and the clubhouse.
III. Identification of the constraints
The constraints of the task are grouped into two; frost we have the resource constraint
which include the total land area to be covered by the project ad the total project cost.
Second set of constraint consists of the minimum features that an international golf
resort should have.
IV. Writing the objective function and the constraints as mathematical equations
i. The standard clubhouse model
~ 2 ~

Max: 2 x1 +1.5 x2+1.5 x3 +2 x 4+ 1.75 x5 +2.25 x6
Subject to
x1 ≥ 1
x2 ≥ 1
x3 :≥ 2
x4 :≥ 2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥ 70
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 ≥ 36
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 +2 y ≤ 42
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +3500000 y ≤ 20000000
ii. The shareholders’ request
Max: 2 x1 +1.5 x2+1.5 x3 +2 x 4+ 1.75 x5 +2.25 x6+4w
Subject to
~ 3 ~
Subject to
x1 ≥ 1
x2 ≥ 1
x3 :≥ 2
x4 :≥ 2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥ 70
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 ≥ 36
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 +2 y ≤ 42
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +3500000 y ≤ 20000000
ii. The shareholders’ request
Max: 2 x1 +1.5 x2+1.5 x3 +2 x 4+ 1.75 x5 +2.25 x6+4w
Subject to
~ 3 ~
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

x1 ≥ 1
x2 ≥ 1
x3 :≥ 2
x4 :≥ 2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥ 70
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 ≥ 36
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 +4 y ≤ 42
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +6000000 y ≤ 20000000
iii. Option 1
Max: 2 x1 +1.5 x2+1.5 x3 +2 x 4+ 1.75 x5 +2.25 x6+4w
Subject to
x1 ≥ 1
x2 ≥ 1
x3 :≥ 2
~ 4 ~
x2 ≥ 1
x3 :≥ 2
x4 :≥ 2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥ 70
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 ≥ 36
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 +4 y ≤ 42
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +6000000 y ≤ 20000000
iii. Option 1
Max: 2 x1 +1.5 x2+1.5 x3 +2 x 4+ 1.75 x5 +2.25 x6+4w
Subject to
x1 ≥ 1
x2 ≥ 1
x3 :≥ 2
~ 4 ~
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

x4 :≥ 2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥ 70
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 ≥ 36
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 +3.2 y ≤ 42
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +5500000 y ≤ 20000000
iv. Option 2
Max: 2 x1 +1.5 x2+1.5 x3 +2 x 4+ 1.75 x5 +2.25 x6+4w
Subject to
x1 ≥ 1
x2 ≥ 1
x3 :≥ 2
x4 :≥ 2
x5 ≥ 1
~ 5 ~
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥ 70
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 ≥ 36
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 +3.2 y ≤ 42
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +5500000 y ≤ 20000000
iv. Option 2
Max: 2 x1 +1.5 x2+1.5 x3 +2 x 4+ 1.75 x5 +2.25 x6+4w
Subject to
x1 ≥ 1
x2 ≥ 1
x3 :≥ 2
x4 :≥ 2
x5 ≥ 1
~ 5 ~

x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥ 70
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 ≥ 36
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 +4 y ≤ 42
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +5300000 y ≤ 20000000
v. Option 3
Max: 2 x1 +1.5 x2+1.5 x3 +2 x 4+ 1.75 x5 +2.25 x6+4w
Subject to
x1 ≥ 1
x2 ≥ 1
x3 :≥ 2
x4 :≥ 2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
~ 6 ~
x1+ x2 ≤ 4
x3+ x4 ≤ 14
x5+ x6 ≤ 4
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥ 70
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 ≥ 36
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 +4 y ≤ 42
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +5300000 y ≤ 20000000
v. Option 3
Max: 2 x1 +1.5 x2+1.5 x3 +2 x 4+ 1.75 x5 +2.25 x6+4w
Subject to
x1 ≥ 1
x2 ≥ 1
x3 :≥ 2
x4 :≥ 2
x5 ≥ 1
x6 ≥ 1
x1+ x2 ≤ 4
x3+ x4 ≤ 14
~ 6 ~
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide

x5+ x6 ≤ 4
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥ 70
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 ≥ 36
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 +4 y ≤ 42
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +6000000 y ≤ 20500000
Part II
The models were created in the spreadsheets using the Solver add in. The excel file is
accompanying the report.
Part III: Report
~ 7 ~
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≤ 72
5 x1+5 x2 +4 x3 +4 x4 +3 x5 +3 x6 ≥ 70
x1+ x2 +x3 + x4 + x5+ x6 =18
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 ≥ 36
3 x1+3.5 x2 +2 x3 +2.5 x4 +1 x5 +0.75 x6 +4 y ≤ 42
1000000 x1 +1500000 x2+750000 x3 +900000 x4 +600000 x5 +650000 x6 +6000000 y ≤ 20500000
Part II
The models were created in the spreadsheets using the Solver add in. The excel file is
accompanying the report.
Part III: Report
~ 7 ~
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser

A Case study on Cunningham Holdings Limited’s Construction of an International Golf
Resort
~ 8 ~
Resort
~ 8 ~

Introduction
Project overview
The management of a successful business is more than just finding avenues of making
money and selling staff. The managers apart from handling the daily operations of the firm
are also tasked with making decisions that are meant to improve the company’s brand in the
future (Perneger & Agoritsas, 2011). This is what is termed as strategic decision making. The
decisions are made based on the mission and vison of the firm. This is the type of decision
that dictates how the firms’ planning is made so as to ensure the business objectives are met
in the long run. The managers are thus tasked with evaluating probable future occurrence and
acting in manner that will put the company brand name on top in the near future.
In line with the strategic decision-making techniques, this report focuses on the
operations of Cunningham holdings. The company is a family owned enterprise that
specializes in offering hospitality services (Brockmann & Anthony, 2016). Based on its
vision which fronts creating a sustainable product to the communities globally, the firm is
interested in undertaking a golf resort project that is meant to improve local tourism as well
as improve the living standard of the local communities (Kiani & Shadlen, 2009). The
managers of Cunningham are dedicated to running a sustainable firm and are hence
determine to ensure the economical, ecological as well as environmental impact of their
decisions are within the United Nations development goals.
In the past shareholders meeting the CEO of the firm Oscar Cunningham did bring
forward an agenda to construct an international golf resort covering 42 hectares at a cost of $
20 million. Included in this resort would be a clubhouse. According to the management plan a
standard clubhouse is the best fit to accompany the golf resort project. The plan to construct a
standard clubhouse is though not in the interest of the shareholders as the latter has requested
for an exclusive clubhouse at a cost of $ 6 million. The CEO of the company was concerned
this may not be achievable and hence as a senior analysist to the firm I was tasked with
evaluating the available options and presenting a report. This document is therefore meant to
showcase the findings and suggest a recommendation that the managers should adhere to.
~ 9 ~
Project overview
The management of a successful business is more than just finding avenues of making
money and selling staff. The managers apart from handling the daily operations of the firm
are also tasked with making decisions that are meant to improve the company’s brand in the
future (Perneger & Agoritsas, 2011). This is what is termed as strategic decision making. The
decisions are made based on the mission and vison of the firm. This is the type of decision
that dictates how the firms’ planning is made so as to ensure the business objectives are met
in the long run. The managers are thus tasked with evaluating probable future occurrence and
acting in manner that will put the company brand name on top in the near future.
In line with the strategic decision-making techniques, this report focuses on the
operations of Cunningham holdings. The company is a family owned enterprise that
specializes in offering hospitality services (Brockmann & Anthony, 2016). Based on its
vision which fronts creating a sustainable product to the communities globally, the firm is
interested in undertaking a golf resort project that is meant to improve local tourism as well
as improve the living standard of the local communities (Kiani & Shadlen, 2009). The
managers of Cunningham are dedicated to running a sustainable firm and are hence
determine to ensure the economical, ecological as well as environmental impact of their
decisions are within the United Nations development goals.
In the past shareholders meeting the CEO of the firm Oscar Cunningham did bring
forward an agenda to construct an international golf resort covering 42 hectares at a cost of $
20 million. Included in this resort would be a clubhouse. According to the management plan a
standard clubhouse is the best fit to accompany the golf resort project. The plan to construct a
standard clubhouse is though not in the interest of the shareholders as the latter has requested
for an exclusive clubhouse at a cost of $ 6 million. The CEO of the company was concerned
this may not be achievable and hence as a senior analysist to the firm I was tasked with
evaluating the available options and presenting a report. This document is therefore meant to
showcase the findings and suggest a recommendation that the managers should adhere to.
~ 9 ~
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
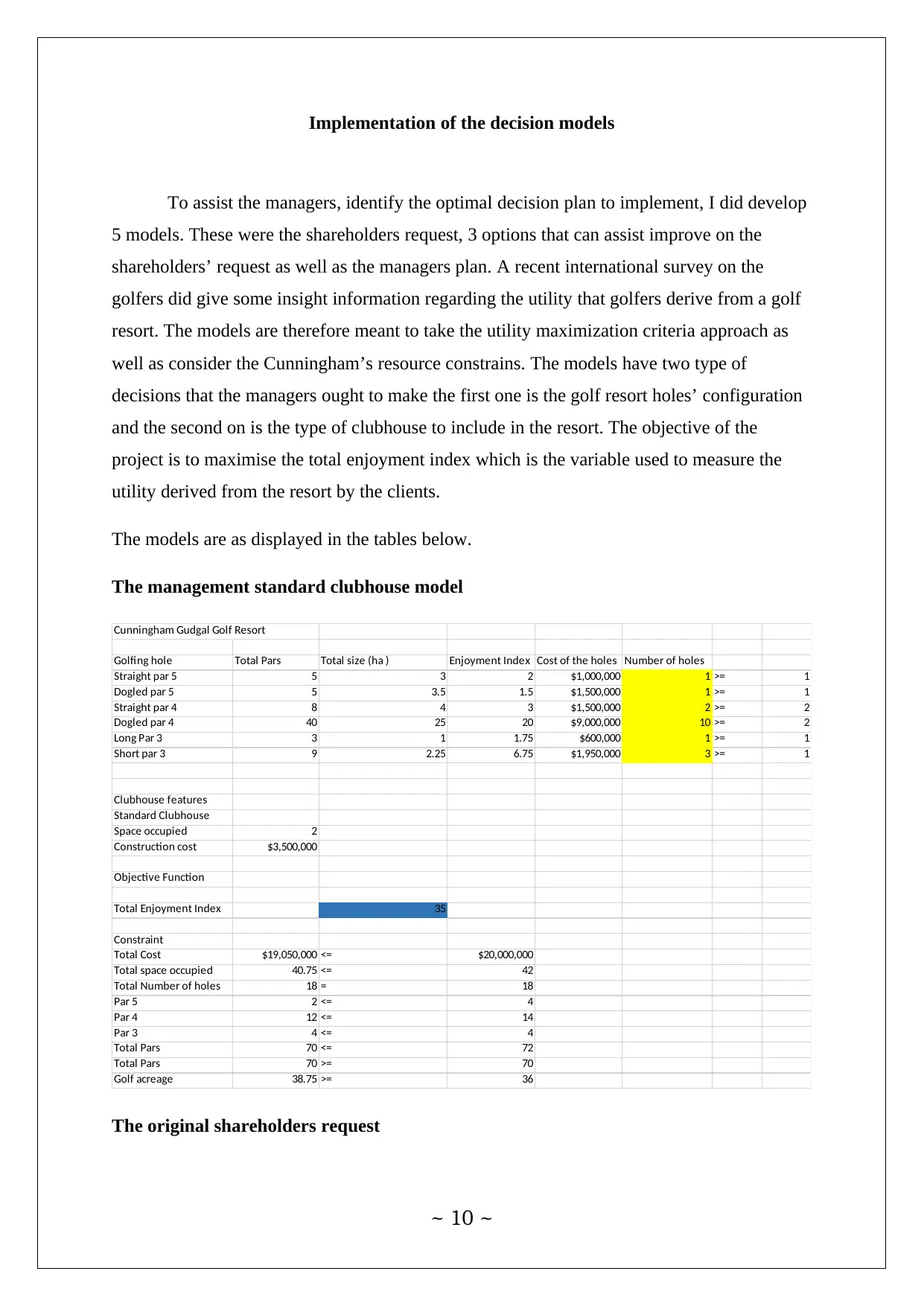
Implementation of the decision models
To assist the managers, identify the optimal decision plan to implement, I did develop
5 models. These were the shareholders request, 3 options that can assist improve on the
shareholders’ request as well as the managers plan. A recent international survey on the
golfers did give some insight information regarding the utility that golfers derive from a golf
resort. The models are therefore meant to take the utility maximization criteria approach as
well as consider the Cunningham’s resource constrains. The models have two type of
decisions that the managers ought to make the first one is the golf resort holes’ configuration
and the second on is the type of clubhouse to include in the resort. The objective of the
project is to maximise the total enjoyment index which is the variable used to measure the
utility derived from the resort by the clients.
The models are as displayed in the tables below.
The management standard clubhouse model
Cunningham Gudgal Golf Resort
Golfing hole Total Pars Total size (ha ) Enjoyment Index Cost of the holes Number of holes
Straight par 5 5 3 2 $1,000,000 1 >= 1
Dogled par 5 5 3.5 1.5 $1,500,000 1 >= 1
Straight par 4 8 4 3 $1,500,000 2 >= 2
Dogled par 4 40 25 20 $9,000,000 10 >= 2
Long Par 3 3 1 1.75 $600,000 1 >= 1
Short par 3 9 2.25 6.75 $1,950,000 3 >= 1
Clubhouse features
Standard Clubhouse
Space occupied 2
Construction cost $3,500,000
Objective Function
Total Enjoyment Index 35
Constraint
Total Cost $19,050,000 <= $20,000,000
Total space occupied 40.75 <= 42
Total Number of holes 18 = 18
Par 5 2 <= 4
Par 4 12 <= 14
Par 3 4 <= 4
Total Pars 70 <= 72
Total Pars 70 >= 70
Golf acreage 38.75 >= 36
The original shareholders request
~ 10 ~
To assist the managers, identify the optimal decision plan to implement, I did develop
5 models. These were the shareholders request, 3 options that can assist improve on the
shareholders’ request as well as the managers plan. A recent international survey on the
golfers did give some insight information regarding the utility that golfers derive from a golf
resort. The models are therefore meant to take the utility maximization criteria approach as
well as consider the Cunningham’s resource constrains. The models have two type of
decisions that the managers ought to make the first one is the golf resort holes’ configuration
and the second on is the type of clubhouse to include in the resort. The objective of the
project is to maximise the total enjoyment index which is the variable used to measure the
utility derived from the resort by the clients.
The models are as displayed in the tables below.
The management standard clubhouse model
Cunningham Gudgal Golf Resort
Golfing hole Total Pars Total size (ha ) Enjoyment Index Cost of the holes Number of holes
Straight par 5 5 3 2 $1,000,000 1 >= 1
Dogled par 5 5 3.5 1.5 $1,500,000 1 >= 1
Straight par 4 8 4 3 $1,500,000 2 >= 2
Dogled par 4 40 25 20 $9,000,000 10 >= 2
Long Par 3 3 1 1.75 $600,000 1 >= 1
Short par 3 9 2.25 6.75 $1,950,000 3 >= 1
Clubhouse features
Standard Clubhouse
Space occupied 2
Construction cost $3,500,000
Objective Function
Total Enjoyment Index 35
Constraint
Total Cost $19,050,000 <= $20,000,000
Total space occupied 40.75 <= 42
Total Number of holes 18 = 18
Par 5 2 <= 4
Par 4 12 <= 14
Par 3 4 <= 4
Total Pars 70 <= 72
Total Pars 70 >= 70
Golf acreage 38.75 >= 36
The original shareholders request
~ 10 ~
Paraphrase This Document
Need a fresh take? Get an instant paraphrase of this document with our AI Paraphraser
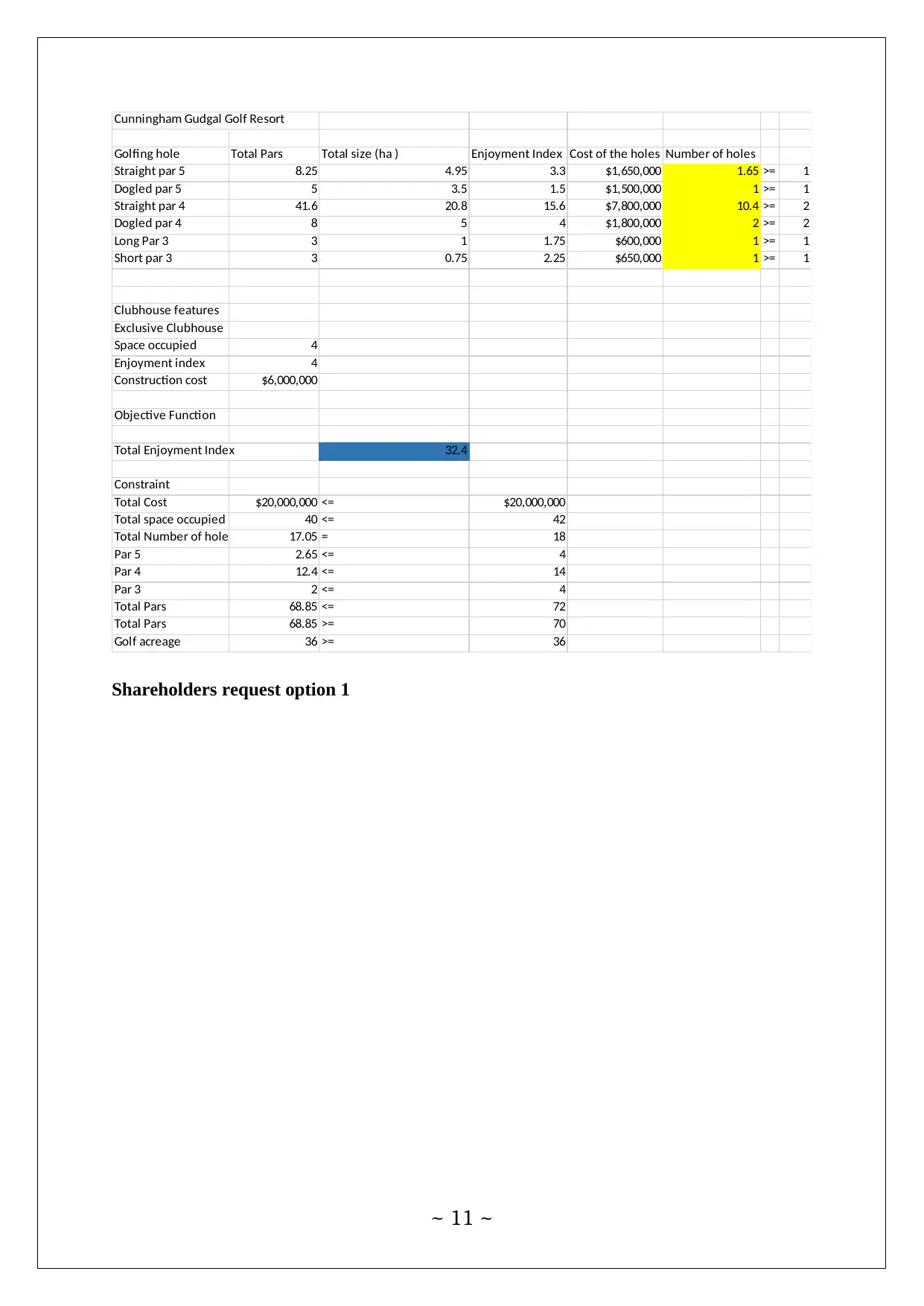
Cunningham Gudgal Golf Resort
Golfing hole Total Pars Total size (ha ) Enjoyment Index Cost of the holes Number of holes
Straight par 5 8.25 4.95 3.3 $1,650,000 1.65 >= 1
Dogled par 5 5 3.5 1.5 $1,500,000 1 >= 1
Straight par 4 41.6 20.8 15.6 $7,800,000 10.4 >= 2
Dogled par 4 8 5 4 $1,800,000 2 >= 2
Long Par 3 3 1 1.75 $600,000 1 >= 1
Short par 3 3 0.75 2.25 $650,000 1 >= 1
Clubhouse features
Exclusive Clubhouse
Space occupied 4
Enjoyment index 4
Construction cost $6,000,000
Objective Function
Total Enjoyment Index 32.4
Constraint
Total Cost $20,000,000 <= $20,000,000
Total space occupied 40 <= 42
Total Number of holes 17.05 = 18
Par 5 2.65 <= 4
Par 4 12.4 <= 14
Par 3 2 <= 4
Total Pars 68.85 <= 72
Total Pars 68.85 >= 70
Golf acreage 36 >= 36
Shareholders request option 1
~ 11 ~
Golfing hole Total Pars Total size (ha ) Enjoyment Index Cost of the holes Number of holes
Straight par 5 8.25 4.95 3.3 $1,650,000 1.65 >= 1
Dogled par 5 5 3.5 1.5 $1,500,000 1 >= 1
Straight par 4 41.6 20.8 15.6 $7,800,000 10.4 >= 2
Dogled par 4 8 5 4 $1,800,000 2 >= 2
Long Par 3 3 1 1.75 $600,000 1 >= 1
Short par 3 3 0.75 2.25 $650,000 1 >= 1
Clubhouse features
Exclusive Clubhouse
Space occupied 4
Enjoyment index 4
Construction cost $6,000,000
Objective Function
Total Enjoyment Index 32.4
Constraint
Total Cost $20,000,000 <= $20,000,000
Total space occupied 40 <= 42
Total Number of holes 17.05 = 18
Par 5 2.65 <= 4
Par 4 12.4 <= 14
Par 3 2 <= 4
Total Pars 68.85 <= 72
Total Pars 68.85 >= 70
Golf acreage 36 >= 36
Shareholders request option 1
~ 11 ~
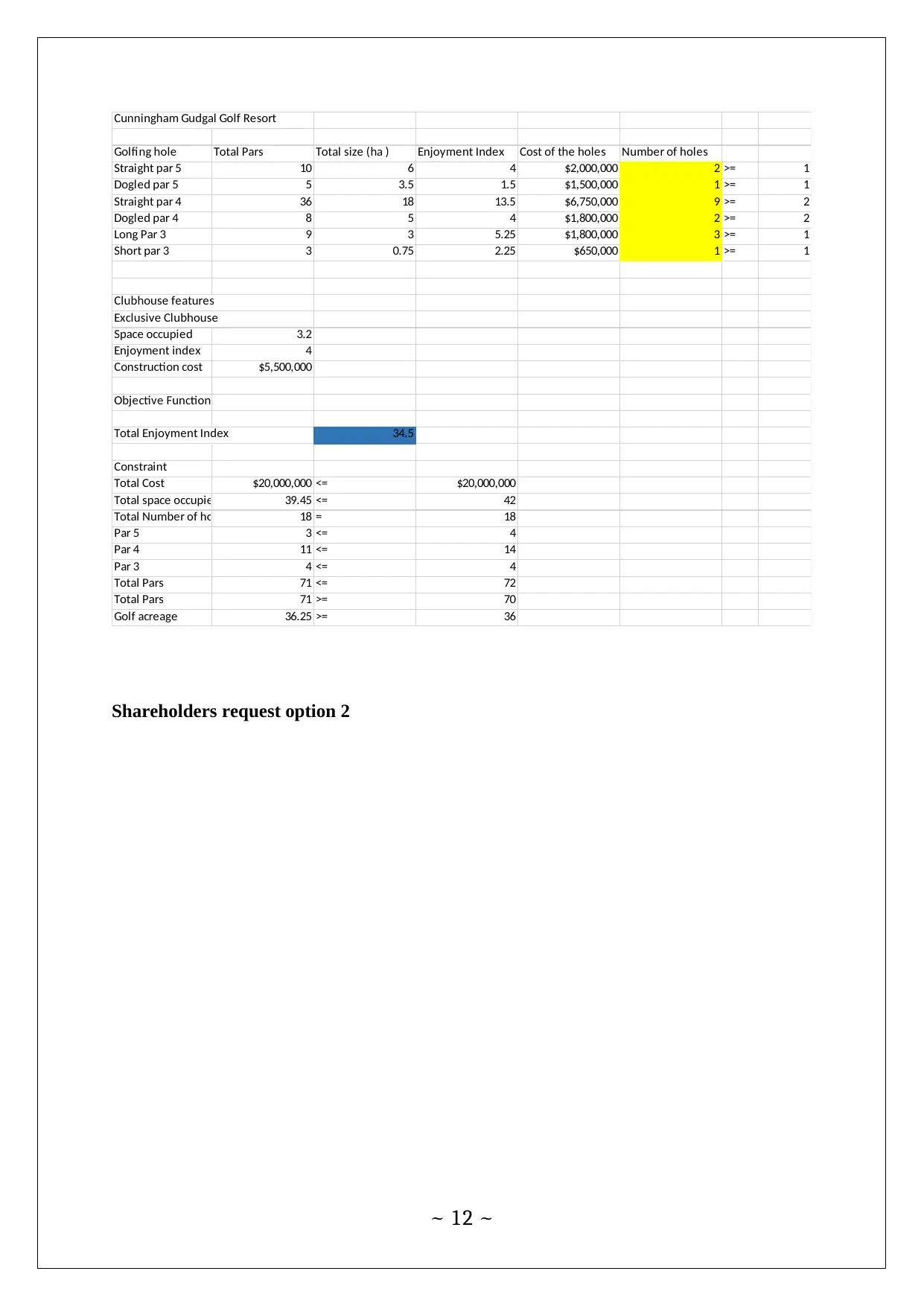
Cunningham Gudgal Golf Resort
Golfing hole Total Pars Total size (ha ) Enjoyment Index Cost of the holes Number of holes
Straight par 5 10 6 4 $2,000,000 2 >= 1
Dogled par 5 5 3.5 1.5 $1,500,000 1 >= 1
Straight par 4 36 18 13.5 $6,750,000 9 >= 2
Dogled par 4 8 5 4 $1,800,000 2 >= 2
Long Par 3 9 3 5.25 $1,800,000 3 >= 1
Short par 3 3 0.75 2.25 $650,000 1 >= 1
Clubhouse features
Exclusive Clubhouse
Space occupied 3.2
Enjoyment index 4
Construction cost $5,500,000
Objective Function
Total Enjoyment Index 34.5
Constraint
Total Cost $20,000,000 <= $20,000,000
Total space occupied 39.45 <= 42
Total Number of holes 18 = 18
Par 5 3 <= 4
Par 4 11 <= 14
Par 3 4 <= 4
Total Pars 71 <= 72
Total Pars 71 >= 70
Golf acreage 36.25 >= 36
Shareholders request option 2
~ 12 ~
Golfing hole Total Pars Total size (ha ) Enjoyment Index Cost of the holes Number of holes
Straight par 5 10 6 4 $2,000,000 2 >= 1
Dogled par 5 5 3.5 1.5 $1,500,000 1 >= 1
Straight par 4 36 18 13.5 $6,750,000 9 >= 2
Dogled par 4 8 5 4 $1,800,000 2 >= 2
Long Par 3 9 3 5.25 $1,800,000 3 >= 1
Short par 3 3 0.75 2.25 $650,000 1 >= 1
Clubhouse features
Exclusive Clubhouse
Space occupied 3.2
Enjoyment index 4
Construction cost $5,500,000
Objective Function
Total Enjoyment Index 34.5
Constraint
Total Cost $20,000,000 <= $20,000,000
Total space occupied 39.45 <= 42
Total Number of holes 18 = 18
Par 5 3 <= 4
Par 4 11 <= 14
Par 3 4 <= 4
Total Pars 71 <= 72
Total Pars 71 >= 70
Golf acreage 36.25 >= 36
Shareholders request option 2
~ 12 ~
⊘ This is a preview!⊘
Do you want full access?
Subscribe today to unlock all pages.

Trusted by 1+ million students worldwide
1 out of 17
Related Documents
Your All-in-One AI-Powered Toolkit for Academic Success.
+13062052269
info@desklib.com
Available 24*7 on WhatsApp / Email
![[object Object]](/_next/static/media/star-bottom.7253800d.svg)
Unlock your academic potential
Copyright © 2020–2026 A2Z Services. All Rights Reserved. Developed and managed by ZUCOL.





